
Voor veel kinderen zijn de redactiesommen groep 6 (ofwel verhaaltjessommen) uit de Cito-toetsen groep 6 lastig. Soms lukt het prima met de ‘kale sommen’, maar zodra eenzelfde soort som in de vorm van een verhaaltje wordt aangeboden, treedt er verwarring op.
De Cito-toetsen rekenen groep 6 bestaan voor de helft uit verhaaltjessommen. Ik geef in dit artikel een paar tips. Als je die met je kind doorneemt, kan dit helpen de redactiesommen in groep 6 beter te begrijpen.
Werk met een stappenplan
Veel kinderen hebben de neiging om het verhaal in de som te zien als onnodige extra informatie. Ze zoeken snel de getallen in het verhaal op en gaan daar dan mee ‘goochelen’.
Voorbeeld:
In een doos zitten 24 bonbons. Tom deelt 6 bonbons uit. Hoeveel houdt hij er over?
Zeker als er net volop geoefend is met tafels, zien veel kinderen in deze som al snel de getallen 24 en 6, en het woord delen. Het antwoord wordt dan al gauw 24 : 6 = 4.
Als je met je kind oefent met redactiesommen, leg dan de nadruk op het verhaal in de som. Gebruik onderstaand stappenplan.
Rekenbox – Tafels van Vermenigvuldiging
Oorspronkelijke prijs was: 72,89.59,00Huidige prijs is: 59,00.
Stappenplan verhaalsommen
- Lees de hele som goed door.
- Probeer er in je hoofd een plaatje bij te maken.
- Zorg dat je goed begrijpt wat de vraag precies is.
- Bedenk welke informatie je nodig hebt om op deze vraag antwoord te geven.
- Kom je er niet uit? Teken de som of maak er een schema bij.
- Markeer of onderstreep de informatie die je nodig hebt.
- Schrijf de complete som op die je moet uitrekenen.
- Bedenk hoe je hem gaat uitrekenen. Kun je een verhoudingstabel gebruiken? Vervang de moeilijke getallen even door makkelijke. Vaak zie je dan opeens hoe je het moet uitrekenen.
- Reken de som uit.
- Controleer je antwoord! Is het antwoord logisch? Controleer een deling door de omgekeerde (keer)som. Controleer een aftreksom door de omgekeerde (optel)som.
Vervang moeilijke getallen eventueel tijdelijk door makkelijke, zodat je kind zich kan focussen op het verhaal in de som.
Voorbeeld:
Er staan 16 stapels met 9 tegels. Henk wil hier 6 stapels van maken. Hoeveel tegels gaan er dan in een stapel?
De eerste 5 stappen zijn hier niet zo moeilijk. Je kind kan eventueel de 16 stapels schematisch tekenen.

Vanuit dit schema zijn verschillende strategieën mogelijk.
- Eerst 6 stapels maken van 18. Dan zijn er nog 4 stapels van 9 over, dus 36 tegels. Op iedere stapel dus 6 tegels erbij, totaal 24 tegels per stapel.
- Je kunt 8 stapels maken van 18, dus ook 18 stapels van 8. Als je daar weer 6 stapels van maakt, worden ze 3 keer zo hoog, dus 3 x 8 = 24.
Komt je kind niet verder met dit schema? Vervang dan de getallen door makkelijke getallen.
Bijvoorbeeld:
Er staan 6 stapels met 10 tegels. Henk wil hier 3 stapels van maken.
Je kind snapt waarschijnlijk nu wel dat je eerst moet weten hoeveel tegels er zijn, en dan dat totaal moet delen door 3. De complete som wordt dan dus:
6 x 10 = …. : 3 = … Uitwerking: 6 x 10 = 60 : 3 = 20.
Terug naar de moeilijke som: markeer de getallen (9 en 16) en schrijf de hele som op die je nu moet uitrekenen. Net als in de makkelijke som wordt het totaal dus uitgerekend door het aantal stapels met het aantal stenen te vermenigvuldigen. Daarna wordt het totaal gedeeld door het nieuwe aantal stapels. De complete som wordt dus:
16 x 9 = ….. : 6 = Uitwerking: 16 x 9 = 144 : 6 = 24
Laat je kind altijd eerst de complete som opschrijven. Het hoeft dan niet meer naar het verhaal te kijken. Er staat alleen nog maar een kale som. Hiermee voorkom je dat je kind, na het uitrekenen van die moeilijke vermenigvuldiging, vergeet dat die uitkomst ook nog gedeeld moet worden.
Leer je kind om het antwoord altijd te controleren. In dit geval zijn er dus 6 stapels van 24 stenen. 6 x 24 = 144, dus het totaal aantal tegels is inderdaad hetzelfde gebleven.
Een verhaalsom wordt dus makkelijker door hem te tekenen, en eventueel grote moeilijke getallen eerst even te vervangen door makkelijke getallen.
Verhaalsommen met breuken
Ook bij de sommen met breuken is ‘tekenen’ het toverwoord. Gebruik daarbij altijd de taart/pizzavorm, dus een cirkel. In veel breuken groep 6 methodes wordt ook een strook gebruikt. Maar je ziet bij een strook niet gelijk of de hele strook is getekend, of een deel ervan. Een complete cirkel is altijd een geheel.
- Oefen met je kind eerst de halven, kwarten, achtsten, zestienden enz. door steeds alle stukken te halveren.
- Oefen dan de derden: een puntje in het midden, en dan het v-teken. Door deze stukken te halveren krijg je zesden, en door ze in 3 stukken te delen krijg je negenden.
- De vijfden zijn lastiger. Weer een puntje in het midden, en dan stukken die iets kleiner zijn dan de kwarten. Halveer de stukken en je krijgt tienden.
Door al dit geteken gaat je kind steeds meer begrijpen wat breuken eigenlijk zijn, en gaat het bijvoorbeeld snappen dat de noemer groter wordt naarmate de stukken kleiner worden.
Een voorbeeld van een verhaalsom met breuken:
In een regenton zit 66 liter water. Hij is voor ¾ gevuld. Hoeveel water kan er totaal in de ton?

Deze opgave is heel makkelijk op te lossen door hem te tekenen:
Nu zie je gelijk: ¾ = 66 l. ¼ is dus 22 l. Er kan 4 x 22 l = 88 l water in de ton.
Een beroemde is deze:
Er moet een schutting gemaakt worden van 1,80 m hoog. 1/3 stuk van de palen moet in de grond komen. Hoe lang moeten de palen zijn?

Als je deze opgave niet tekent, kom je al gauw tot de (foute) conclusie dat de palen 2,40 moeten zijn (1,80 m + 1/3 daarvan). Tekenen geeft de goede oplossing:
Je ziet hier dat 1/3 paal 0,90 cm is. De hele paal moet dan dus 1,80 m + 0,90 m = 2,70 m zijn.
Een ander voorbeeld van een verhaalsom met breuken:
5 kinderen verdelen 4 pizza’s. Ieder kind krijgt dus ….. deel van de pizza.

Teken de pizza’s.
Ieder kind krijgt 1/5 van iedere pizza, dus in het totaal 4/5.
Rekenen met de verhoudingstabel
In groep 6 leert je kind rekenen met een verhoudingstabel. Heel veel opgaven zijn op te lossen met zo’n tabel.
- Sommen met het woordje ‘per’ erin. Euro per stuk, km per uur, snoepjes per kind, schepjes suiker per liter enzovoorts.
- Sommen met breuken
- Schaalsommen
- Sommen met procenten
Een paar voorbeelden:
Mark doet 5 uur over 200 km. Rianne rijdt dezelfde afstand in 4 uur. Hoeveel km per uur rijdt Rianne sneller dan Mark?
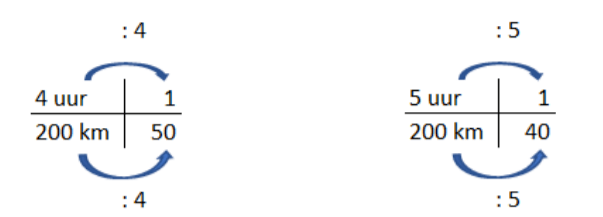
Om dit op te lossen moet je dus weten hoeveel km per uur Mark en Rianne rijden.
Hier zie je dus dat Rianne 10 km harder rijdt per uur.
Voor 3 kilo aardappelen betaal ik € 1,80. Hoeveel moet ik dan betalen voor 11 kilo?

Door de getallen in een verhoudingstabel te zetten, wordt gelijk duidelijk hoe het uitgerekend moet worden. Eerst 1 kilo uitrekenen, dan keer 11 doen.
Op de plattegrond van een tuin is het pad 3 cm. De schaal van de tekening is 1:200. Hoelang is het pad in het echt?
Meer voorbeelden staan in het artikel over verhaaltjessommen. Bekijk hier de uitleg over verhoudingstabellen.
Verhaalsommen met tijd
Veel kinderen hebben moeite met deze sommen. Dit komt onder andere doordat ze gewend zijn om in het tientallig stelsel te rekenen, waarin je getallen onder elkaar zet om ze op te tellen of af te trekken. Een halve euro plus een kwart euro kun je uitrekenen door er een kommagetal van te maken: € 0,50 + € 0,25 = € 0,75.
Maar een half uur plus een kwart uur kun je zo niet uitrekenen, omdat een half uur geen 50 minuten is maar 30. Dat is één van de redenen dat kinderen hier veel fouten in maken, zeker als de tijden digitaal zijn. Ze lijken dan nog meer op gewone getallen, en het ligt dan voor de hand om ze ook op te tellen als gewone getallen.
In verhaalsommen worden dan ook vaak nog de gewone kloktijden en digitale tijden gecombineerd.
Karel gaat een fietstocht maken. Hij fietst 25 km per uur. De tocht is 125 km, en hij houdt 2 keer een half uur pauze. Hij vertrekt om 9:30 uur. Hoe laat komt hij aan?
Er staan in deze som veel getallen en je kind ziet al gauw door de bomen het bos niet meer. Je kan het helpen door te vragen: als ik ergens naar toe ga en ik wil weten hoe laat ik aankom, wat moet ik dan weten? Met die vraag help je je kind om het verhaal te visualiseren. Het antwoord is dan natuurlijk dat je moet weten hoe laat je vertrekt, en hoe lang je erover doet.
Als som ziet dat er zo uit: 9:30 + ? = …

Nu moet je dus alleen nog weten wat er op de plek van het vraagteken komt. Maak eventueel een verhoudingstabel:
Het is dan snel duidelijk dat Karel 5 uur fietst. Daar moet nog 2 keer een half uur pauze, in totaal dus 1 uur, bij worden opgeteld. In totaal doet Karel er 6 uur over. Nu moet die 6 uur nog bij de 9:30 geteld worden. In dit geval is dat makkelijk, want je kunt die 6 uur gewoon bij de 9 optellen, en dat wordt dan 15:30 uur.
Lastiger wordt het als over hele uur heen gerekend moet worden, zoals in de volgende opgave:
De voorstelling begint om kwart voor 2. Op het bord bij de ingang staat dat de voorstelling 90 minuten duurt, en dat er ook nog een pauze in zit van 20 minuten. Hoe laat is de voorstelling afgelopen?
Laat je kind eerst weer opschrijven wat het precies moet uitrekenen, dus:
Kwart voor 2 + 90 minuten + 20 minuten =

Door een soort getallenlijn te gebruiken maak je het nu overzichtelijk:
Omtrek en oppervlakte
Verhaalsommen over omtrek en oppervlakte zijn ook altijd makkelijker op te lossen door ze te tekenen.
Voorbeeld:
De tuin van Tom is 20 bij 30 meter. Tom wil overal tegels leggen van 50 bij 50 cm. Alleen in het midden komt een vijver van 4 bij 4. Hoeveel tegels moet hij kopen?

20 m = 40 tegels
30 m = 60 tegels
Er passen 2 tegels op een meter, dus 40 op 20 meter, en 60 tegels op 30 meter. Er komen dus 40 rijen van 60 tegels. Op 4 m passen 8 tegels, dus er moeten 8 x 8 tegels afgetrokken worden van het totaal. De kale som wordt dus:
40 x 60 = …… – 8 x 8 = ….. Uitwerking: 40 x 60 = 2400 – 64 = 2336.
Schattend rekenen: ongeveer
Een woord dat in veel sommen terugkomt, is het woord ‘ongeveer’. Deze sommen vallen onder het ‘schattend rekenen’. Schattend rekenen wordt steeds belangrijker. Zeker scholieren op het voortgezet onderwijs gebruiken zelfs voor de makkelijkste sommen de rekenfunctie van hun telefoon. Een foutje is dan zo gemaakt: een getal verkeerd intikken of aflezen, of een komma die verkeerd geplaatst is. Door je kind nu al te leren om altijd, vooraf of achteraf, het antwoord te schatten, worden deze fouten snel ontdekt.
Hieronder is een voorbeeldopgave met ‘ongeveer’ in het verhaaltje (bron: oefenboek rekenen groep 6 – 2e helft schooljaar):
Alle groepen van de bovenbouw hebben geld ingezameld voor de slachtoffers van een natuurramp. De groepen hebben het volgende ingezameld:
Groep 6: € 1045
Groep 7: € 975
groep 8: € 952Hoeveel hebben de groepen gezamenlijk ongeveer ingezameld?
a. € 2000
b. € 2500
c. € 3000
d. € 3500
De sommen met ‘ongeveer’ in de tekst zijn sommen die onder de categorie ‘schattend rekenen’ vallen. Deze sommen moeten op de Cito-toets doorgaans zonder kladpapier worden uitgerekend. Als je kind zo’n som moet oplossen, is het handig om het volgende te onthouden:
Eerst afronden en dan pas uitrekenen.
Sommige kinderen gaan eerst de getallen (uit het hoofd) bij elkaar optellen. Hier doen ze lang over of ze lopen vast. Het is dus van belang om de getallen die je bij elkaar moet optellen eerst af te ronden. De som wordt dan 1000 + 1000 + 1000 = 3000.
Dus: staat er ‘ongeveer’ in het verhaaltje? De getallen eerst afronden en dan pas de som uitrekenen.
Ga aan de slag met oefenen met gratis werkbladen met redactiesommen met ‘ongeveer’ voor rekenen groep 6.

Oefenbladen Rekenen Groep 6 (Gratis)
Of maak ook gebruik van de oefenboeken:














Heel nuttig om dit te bespreken met de kinderen. Dank je wel!👍
Duidelijk !
ik vind het een goed boekje! en ik heb een vraag is er ook een antwoorden blad van het boekje?
Hallo Maaike,
Hartelijk dank voor je mail, met daarin een link over de verhaaltje sommen en het begrip ‘ongeveer’! We gaan er zeker ons voordeel mee doen! Is er ook een site waar ik de Cito-toetsen van voorgaande jaren (gratis) kan raadplegen?? Het boek dat we kunnen bestellen lijkt ons een prima hulpmiddel, maar is nog al een uitgave. In ieder geval fijn dat veel informatie ook op deze site gratis is uitgewerkt.
Beste J.A.,
Er is helaas geen website waar je oude Cito-toetsen kunt inzien. Je zou misschien kunnen beginnen met de gratis oefenbladen? Je kunt ze hier downloaden: https://wijzeroverdebasisschool.nl/werkbladen/rekenen
Succes!
Hartelijke groet,
Carola
Hebben jullie misschien ook tips hoe ze makkelijk kunnen zien of ze moeten delen, vermenigvuldigen, optellen of aftrekken. Mijn dochter van 10 zit in groep 6 en heeft hier heel veel moeite mee. We hebben inmiddels de oefenboeken besteld.
Hallo Chantal, dit is inderdaad een veel voorkomend probleem en geeft aan dat een kind nog niet genoeg inzicht heeft in de som. In de huidige methodes wordt vaak te weinig geoefend met ‘kale’ sommen en moeten de kinderen gelijk aan de slag met verhaaltjessommen. De basis wordt dan niet goed gelegd. Het is belangrijk om eerst veelvuldig te oefenen met ‘kale’ sommen. In de oefenboeken worden eerst kale sommen geoefend en daarna de verhaaltjessommen. Als je de volgorde van de boeken aanhoudt, wordt er een goede basis gelegd. Kijk even aan hoe dit gaat. Mocht je toch nog ergens tegen aan lopen, dan kun je altijd even een e-mail sturen.
Succes!
Hartelijke groet,
Carola
Hallo,
ik ben het helemaal eens met de opvatting dat bij ongeveer sommen eerst moet worden afgerond en daarna pas de bewerking. Ik heb een andere mening over hoe er in het voorbeeld wordt afgerond. In het voorbeeld wordt alles naar 1000 afgerond en dat is volgens mij onjuist. 945 en 902 zouden naar 900 moeten worden afgerond. Dat is het eerste honderdtal dat in aanmerking komt. Nergens staat in de som dat het moet worden afgerond op een 1000-tal
Beste Theo,
Dank voor je bericht. Vaak staat er inderdaad bij of een getal moet worden afgerond op bijvoorbeeld een tiental, honderdtal of duizendtal. Maar bij deze som maakt het niet uit. Het antwoord blijft hetzelfde.
Hartelijke groet,
Carola de Koning
ik vind het perfect bedankt