
Vindt jouw kind redactiesommen, oftewel verhaalsommen, ook zo lastig? In dit artikel over redactiesommen in groep 8 krijg je uitleg en tips, zodat je jouw kind(eren) kunt helpen bij het oplossen van de sommen!
Als jouw kind bij rekenen in groep 8 redactiesommen ook lastig vindt, kan dit verschillende oorzaken hebben. Je kind:
- is een zwakke rekenaar
- is een sterke rekenaar, maar minder goed in begrijpend lezen
- gebruikt de verkeerde taakaanpak
Is je kind een zwakke rekenaar?
Als je kind over de hele linie zwak is in rekenen, is het feit dat je ook nog zelf informatie uit het verhaal en eventueel de afbeeldingen moet halen, een extra uitdaging. Hier speelt vaak ook faalangst mee. De som ziet er anders uit dan normaal, en dat maakt dat faalangstige kinderen gaan twijfelen over de goede aanpak. Ze zien vaak door de bomen het bos niet meer.
Voorbeeld:
Een trein rijdt 90 km/uur. Johan stapt na een kwartier uit. Na hoeveel kilometer is dat?
De som die hier uitgerekend moet worden, is 90 : 4. Dat is voor een kind uit groep 8 geen moeilijke som. Maar de som ziet er ingewikkeld uit. Er moeten verschillende tijdseenheden gecombineerd worden, en als je al aan jezelf twijfelt is het lastig om hier een kale som uit te halen.
In deze opgave staan geen lastige getallen, maar in groep 8 wordt vaak gerekend met kommagetallen en getallen boven de 100.000. Je kunt je kind helpen door het te leren om eerst makkelijke getallen in te vullen. Vaak ziet het dan wel wat de som is die in het verhaal zit, en hoe je die uitrekent.
Bekijk ook:
Ligt het aan het tekstbegrip?
Het kan ook zijn dat je kind best goed is in rekenen. Maar als het minder goed is in begrijpend lezen, dan heeft het misschien ook moeite om de som uit het verhaal te halen. Onderzoek wijst uit dat er een relatie is tussen een zwakke score op begrijpend lezen en op redactiesommen.
Voorbeeld:
Een auto rijdt met een snelheid van 100 km/uur. De afstand die hij moet afleggen is 350 km. Hij vertrekt om 10.00 uur, en houdt 2 keer een pauze van 10 minuten. Hoe laat komt hij aan?
Kinderen die niet goed zijn in begrijpend lezen vinden het vaak moeilijk om zich een voorstelling te maken bij wat ze lezen. In bovenstaande som gaan ze daarom twijfelen: moet je die 20 minuten van die pauzes nu bij de totale reistijd tellen of ervan aftrekken?
Leer je kind om de opgave terug te brengen tot een simpel verhaal: als je onderweg naar school even pauze houdt, kom je dan vroeger of later op school? Later natuurlijk. Dat stukje van de som is dus al opgelost: de pauzetijd moet bij de totale reistijd geteld worden. Voor het berekenen van de reistijd kan een verhoudingstabel gebruikt worden. Zie verderop in het artikel.
Taakaanpak en redactiesommen
Ten slotte zijn er ook kinderen die simpelweg het geduld niet kunnen opbrengen om de hele som te lezen. Ze kijken naar de getallen in de opgave en slaan daarmee gelijk aan het rekenen, zonder te kijken wat de vraag nu precies is. Meestal controleren ze het antwoord ook niet.
Voorbeeld:
Een stuk grond van 60 m bij 40 m wordt voor de helft verkocht voor € 30 per m2. Hoeveel levert het op?
Dit soort kinderen leest 60 m bij 40 m en slaat gelijk aan het rekenen: 60 m x 40 m = 2400 m2 → 2400 m2 x € 30 = € 72000. Dat het land maar voor de helft verkocht wordt, zien ze over het hoofd. Ze gaan gelijk door naar de volgende som, zonder de som nog eens na te lezen of hun antwoord te controleren.
Je kunt je kind helpen door het te leren met onderstaand stappenplan te werken. Je kind zal er eerst weerstand tegen hebben, want het lijkt langer te duren. Maar als het eenmaal gewend is om eerst een plannetje te maken, en dan pas te gaan rekenen, zal duidelijk worden dat het geen extra tijd kost, omdat je niet steeds opnieuw de tekst hoeft te lezen voordat je de volgende stap kan zetten. Vindt je kind het toch moeilijk om niet gelijk aan het rekenen te slaan? Vervang de getallen van de opgave dan eerst door letters of andere symbolen. Op die manier wordt je kind gedwongen om eerst naar het verhaal zelf te kijken.
Voorbeeld:
De school koopt 250 pennen voor € 50 euro. Hoe duur is één pen?
Jouw ongeduldige kind zal waarschijnlijk die 250 delen door 50, dus 5 euro per stuk.
Vervang je de getallen door letters, dan staat er:
De school koopt x pennen voor € b. Hoe duur is één pen.
Je kind bedenkt dan wel dat het bedrag b gedeeld moet worden door x pennen (en niet andersom).
Stappenplan redactiesommen groep 8
In groep 8 wordt verwacht dat alle lastige onderdelen uit groep 7 beheerst worden, en worden in de redactiesommen, of verhaalsommen, vaak combinaties gemaakt. Bij het voorbeeld van de auto hierboven moet bijvoorbeeld rekenen met tijd gecombineerd worden met de kennis over verhoudingen (km/uur).
Wat in alle gevallen goed is, is het werken met een vast stappenplan.
Het stappenplan

Voorbeeld:
Een groenteman koopt 2000 sinaasappelen voor 25 cent per stuk. Bij thuiskomst blijken er 100 beschimmeld te zijn. De rest verkoopt hij voor 40 cent per stuk. Hoeveel euro winst heeft hij?
Veel kinderen beginnen meteen te rekenen als ze zo’n verhaalsom zien, in de volgorde waarin ze het lezen. Maar het gevaar is dat ze dan de 100 beschimmelde sinaasappels vergeten, of gewoon niet weten wat ze met dat getal 100 moeten doen doordat ze zich geen voorstelling maken bij de som. Of ze vergeten om de centen om te rekenen naar euro’s.
Met het stappenplan los je deze som als volgt op:
- Doorlezen en plaatje maken in je hoofd:
- Dan is gelijk duidelijk dat de groenteman wel betaalt voor de beschimmelde sinaasappels maar ze vervolgens thuis weggooit, en dus 100 sinaasappels minder verkoopt. Ziet je kind het toch niet in één keer, laat het dan stapje voor stapje tekenen wat er staat.
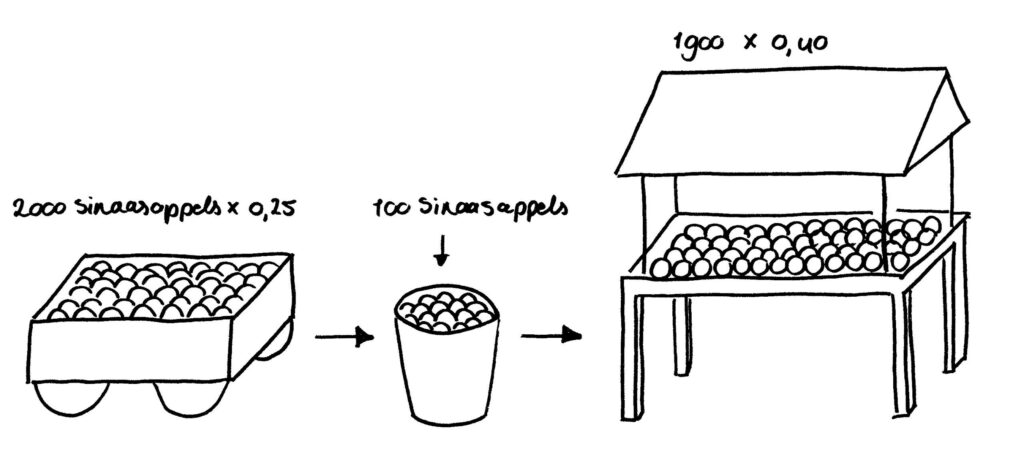
2. Lees de vraag:
- Er wordt gevraagd naar de winst. Winst is het verschil tussen het bedrag waarvoor is gekocht is en waarvoor het verkocht wordt. In dit geval moeten die bedragen nog uitgerekend worden.
3. Bedenk welke informatie nodig hebt.
4. De volgende gegevens worden onderstreept.
- Een groenteman koopt 2000 sinaasappelen voor 25 cent per stuk. Bij thuiskomst blijken er 100 beschimmeld te zijn. De rest verkoopt hij voor 40 cent per stuk. Hoeveel euro winst heeft hij?
5. Schrijf de complete som op:
- verkoopprijs – inkoopprijs = winst
- 1900 x 40 cent – 2000 x 25 cent = …. Cent = € ….
6. Bedenk hoe je de som gaat uitrekenen:
- Door ze eerst een compleet plannetje te laten opschrijven, en dan pas te gaan rekenen is het risico kleiner dat wordt vergeten om het antwoord om te rekenen naar euro’s.
7. Reken de som uit:
- Ze concentreren zich dan eerst op het verhaal, en kunnen zich daarna concentreren op het rekenen, zonder nog een keer naar de tekst te hoeven kijken.
8. Controleer het antwoord:
- Pas als het antwoord is uitgerekend, hoeven ze pas terug te kijken naar de opgave om hun antwoord te controleren.
Hoe kun je controleren?
Veel kinderen controleren zichzelf door nog een keer dezelfde som uit te rekenen. Maar de kans dat er dan in dezelfde valkuil getrapt wordt (als het antwoord fout is), is groot. Op welke manier controleer je jezelf dan wel?
- Laat je kind bedenken of het een logisch antwoord is;
- Was er een andere manier om (evt. schattend) aan het antwoord te komen. Bijvoorbeeld: 15 cent winst per sinaasappel. 2000 x 15 = 15.000 cent – de beschimmelde sinaasappels. Kloppen de uitkomsten (ongeveer) met elkaar?;
- Klopt het als je de uitkomst invult in het verhaal (zie voorbeeld hieronder);
- Zo niet, kijk of er een rekenfout is gemaakt.
In dit geval is het duidelijk hoe de som uitgerekend moet worden. Er staan gewoon 2 keersommen, en als je het antwoord hebt, moet je het verschil ertussen uitrekenen met een minsom.
Dit is anders met de volgende opgave:
De slager heeft 60 kg vlees verkocht voor € 260. Hij had € 20 winst. Wat heeft hij voor 1 kg betaald?
De winst is hier gegeven. Eerst moet dus de informatie die je daarvoor hebt gemarkeerd worden.
In dit geval is de winst en de verkoopprijs bekend, en moet de inkoopprijs berekend worden. De inkoopprijs is de verkoopprijs – de winst, dus de som die dan uitgerekend moet worden is:
€ 260- € 20= ? ? : 60 = € (240:60=4)
In dit geval kan je kind het antwoord controleren, door het verhaal om te draaien en de uitkomst in te vullen.
Dus:
De slager betaalt € 4,- voor 1 kilo, dus € 240,- voor 60 kilo, en verkoopt het met € 20 winst, dus bij elkaar € 260.
Redactiesommen groep 8: vaste modellen
Het stappenplan kan je kind helpen om de som uit het verhaal te halen. Daarnaast kan het je kind helpen om een vaste manier te gebruiken om de som vervolgens uit te rekenen.
Verhoudingstabel
De verhoudingstabel is een voorbeeld van zo’n vaste manier. Deze kan gebruikt worden bij opgaven over afstand/tijd/snelheid, procenten, gewicht en schaal, maar ook alle sommen waarbij sprake is van een verhouding. Het woordje per is een duidelijk signaalwoord: hier kunnen verhoudingstabellen gebruikt worden. Het is een makkelijke manier om informatie uit een verhaalsom snel overzichtelijk te maken. Een paar voorbeelden:
Voorbeeld procenten
Karin koopt een racefiets, en heeft daarna nog maar 8% over van haar spaargeld. Dat is € 16,- . Hoe duur was de fiets?
Stappenplan:
Eerst lezen en een voorstelling maken, eventueel tekenen. Eerst een volle spaarpot, daarna nog maar 8% over en dat is € 16. Je moet dus eerst weten hoeveel er eerst in de spaarpot zat (100%) en dan die € 16 eraf trekken om te zien hoeveel er aan de fiets is uitgegeven. We ordenen de getallen in de verhoudingstabel en maken het plannetje af, want het antwoord in de verhoudingstabel is nog niet het antwoord op de vraag.
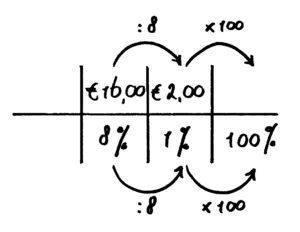
? – € 16 = ………
Voorbeeld schaal
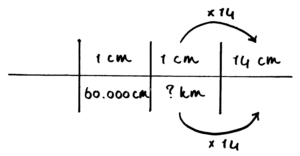
Van plaats A naar B is op de kaart 14 cm. De schaal van de kaart is 1 : 60.000. Hoeveel km is de afstand in het echt?
Schaalsommen zijn altijd lastig, omdat het gaat om de verhouding in centimeters. We vullen eerst de getallen in zoals ze in de som staan. Je kunt dan gelijk vermenigvuldigen met 14 maar omdat het antwoord in km moet worden gegeven is het handiger om eerst om te rekenen naar kilometers.
Door alles eerst in de tabel in te vullen, is duidelijk welke stappen gezet moeten worden en in welke volgorde.
Voorbeeld km/uur
Een auto rijdt met een snelheid van 100 km/uur. De afstand die hij moet afleggen is 350 km. Hij vertrekt om 10.00 uur, en houdt 2 keer een pauze van 10 minuten. Hoe laat komt hij aan?
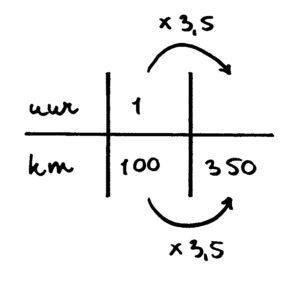
Het complete plannetje wordt nu:
10:00 + reistijd + 20 minuten =
Voorbeeld … euro per…
De aardbeien kosten € 3,50 per kilo. Hoeveel is dat voor 150 gram?
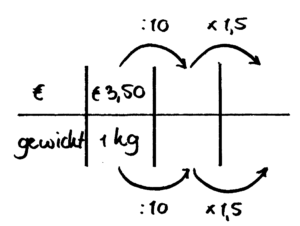
Bij deze som is het handig als je kind makkelijk maten omrekent, in dit geval dus 1 kg:10 = 100 gram.
Meer uitleg over het metriek stelsel vind je hier.
Redactiesommen: andere vaste modellen
Als het gaat om oppervlakte en omtrek is het altijd aan te raden om eerst een tekening te maken van de situatie.
Voorbeeld:
De kamer is 75 m2. De lengte is 15 m. Wat is de omtrek?
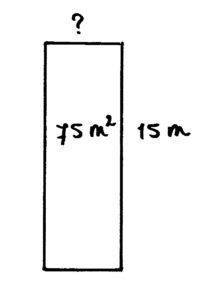
Een tekening geeft gelijk duidelijkheid.
Het plannetje wordt:
75: 15 = ?. Omtrek is 2 x 15 + 2 x ?
Breukmodel
Er zijn ook sommen zoals:
In een regenton zit nog 30 liter water. Er is 3/5 deel uitgehaald. Hoeveel water kan er in de ton?
Bij deze som geeft het duidelijkheid als je de regenton tekent.
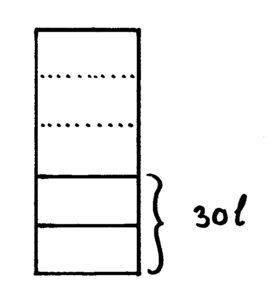
Je ziet gelijk:
2/5 = 30 l. 1/5 is dus 15 l
5/5 is 5 x 15 liter=75 liter
Bij andere sommen met breuken kan het helpen om een breukencirkel of breukenstrook te tekenen.
Johan zegt: als ik 2/7 deel van mijn geld uitgeef, heb ik nog 10 euro over. Hoeveel geld heeft Johan?
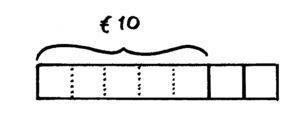
Uit de tekening blijkt weer duidelijk:
5/7 is € 10
1/7 is dus €2. 7/7 is € 14
Nog een voorbeeld:
Strookmodel
Luuk en Yasmin verdelen 64 knikkers. Yasmin krijgt 3 keer zoveel als Luuk. Hoeveel krijgt Luuk?
Bij dit soort sommen is het altijd handig om een strookmodel te maken:
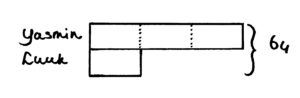
Nu wordt gelijk duidelijk:
1 deel is 64 :4=16. Yasmin krijgt 3×16=48 en Luuk 16 knikkers
Door veel te oefenen met het stappenplan, het tekenen en de schema’s help je je kind om ook die ingewikkelde verhaalsommen in groep 8 op te lossen!
Veel succes ermee!
Ook lezen over redactiesommen in andere groepen?
- Redactiesommen groep 3
- Redactiesommen groep 4
- Redactiesommen groep 5
- Redactiesommen groep 6
- Redactiesommen groep 7

Oefenbladen Doorstroomtoets Groep 8 (Gratis)





Jullie zeggen geen antwoord dat vind ik raar 🧐
Beste Rina,
In onze oefenbladen en oefenboeken staan sommen met antwoorden.
De oefenbladen voor groep 8 kun je hier gratis downloaden:
https://wijzeroverdebasisschool.nl/werkbladen/groep-8
Hartelijke groet,
Carola
Heel goed uitleggen super bedankt
Zeer heldere uitleg, precies aansluitend bij de moeilijkheden van veel leerlingen bij verhaaltjessommen. Meteen toepasbaar, naadloos aansluitend op de sommen die in groep 8 behandeld worden! Dank je wel!
Heel nuttig en duidelijk omschreven. Nu nog oefenen en kijken of deze manier van uitleg ook bij mijn dochter (11) aanslaat.