
Heb je wel eens van het metriek stelsel gehoord? Dat is een moeilijke naam voor een heel handige rekenhulp!
In dit artikel leggen we je alles uit over het metriek stelsel. Zo leer je hoe het is opgebouwd, hoe je zelf een metriek stelsel tekent en hoe je ermee kunt rekenen. Je weet straks ook hoe je meters, liters en grammen moet omrekenen naar andere maateenheden.
Wat is het metriek stelsel?
Het metriek stelsel is een systeem waarmee je meet hoe zwaar, ver of groot iets is.
Vroeger had iedere regio zijn eigen meetsysteem, waardoor het moeilijk was om informatie met elkaar uit te wisselen. Daarom werd in de Franse Revolutie (rond het jaar 1790) het metriek stelsel bedacht. Wereldwijd gebruiken nu bijna alle landen dezelfde afmetingen, zoals meters, kilogrammen en liters. Wel zo makkelijk!
In een metriek stelsel gebruik je verschillende maateenheden. Een maateenheid geeft aan:
- hoe groot iets is;
- hoe zwaar iets is;
- of welke hoeveelheid ergens in past.
Wij kennen 3 verschillende maten bij het rekenen. Dat zijn:
- Allerlei maateenheden rondom de ‘meter’, om te kunnen meten hoe lang of hoe ver iets is. Denk maar aan kilometer, centimeter, millimeter en nog veel meer.
- Maateenheden rondom ‘grammen’, om te kunnen meten hoe zwaar iets is. Een paar voorbeelden: kilogram, gram en milligram.
- Maateenheden rondom ‘liters’, om aan te geven welke hoeveelheid ergens in kan. Bijvoorbeeld: milliliter, centiliter, deciliter.
Het is heel handig om het metriek stelsel te kennen, omdat je het overal nodig hebt!
Als de kapper ‘een paar centimeter’ van je haar gaat knippen, is het wel fijn te weten hoeveel dat ongeveer is.
En als je cupcakes gaat bakken is het wel handig dat je snapt hoeveel gram boter en zout er in je beslag moeten. Je wilt straks immers wel cupcakes die lekker smaken!
Bekijk ook:
- Maten omrekenen: een handig ezelsbruggetje
- Meten en meetkunde: 5 handige weetjes
- Km naar m omrekenen
- Oppervlakte berekenen
- Inhoud berekenen
- Schaal berekenen
Metriek stelsel schema
Het metriek stelsel is eigenlijk een soort schema en ziet er altijd uit als een trap. Zo’n trap ziet er ongeveer zo uit:
Elke trede van de trap staat voor 1 maateenheid, bijvoorbeeld meter, decimeter of centimeter.
Kijk maar eens naar dit voorbeeld, waarin het metriek stelsel voor lengtematen (meters) te zien is:
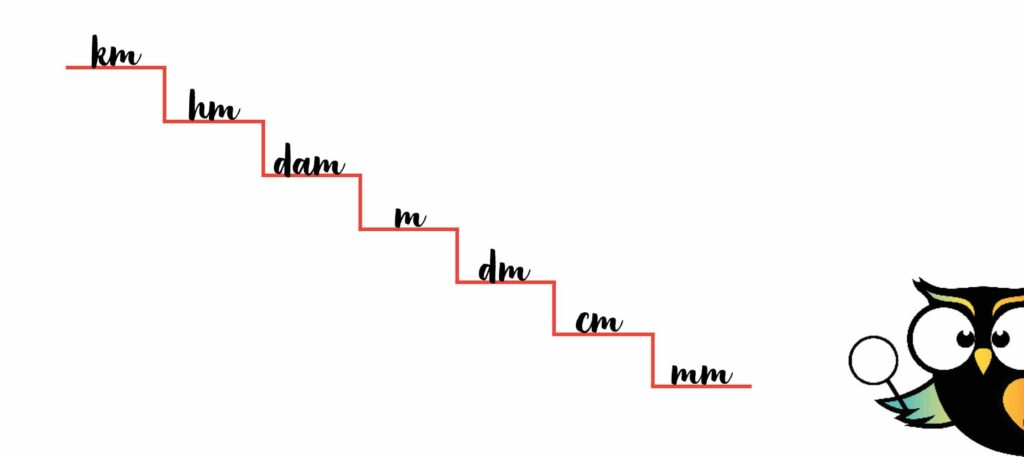
Voor andere maten, zoals liters en grammen, kun je ook dit soort trappen maken.
Voordat we precies uitleggen hoe je het metriek stelsel kunt gebruiken voor je rekensommen, vertellen we je eerst meer over het metriek stelsel van de meters.

Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 5 (Gratis)

Oefenbladen Rekenen Groep 6 (Gratis)

Oefenbladen Rekenen Groep 7 (Gratis)
Metriek stelsel van meters
We beginnen weer met een lege trap.

Die trap gaan we vullen met alle maateenheden die bij de lengtematen (meters) horen.
De kleinste maateenheid van dit metrieke stelsel is de millimeter. Een voorbeeld van de millimeter vind je gewoon aan je hand! Je nagel is namelijk ongeveer een millimeter dik.
Millimeter schrijf je als ‘mm’ en zet je rechts op de onderste trede van de trap.
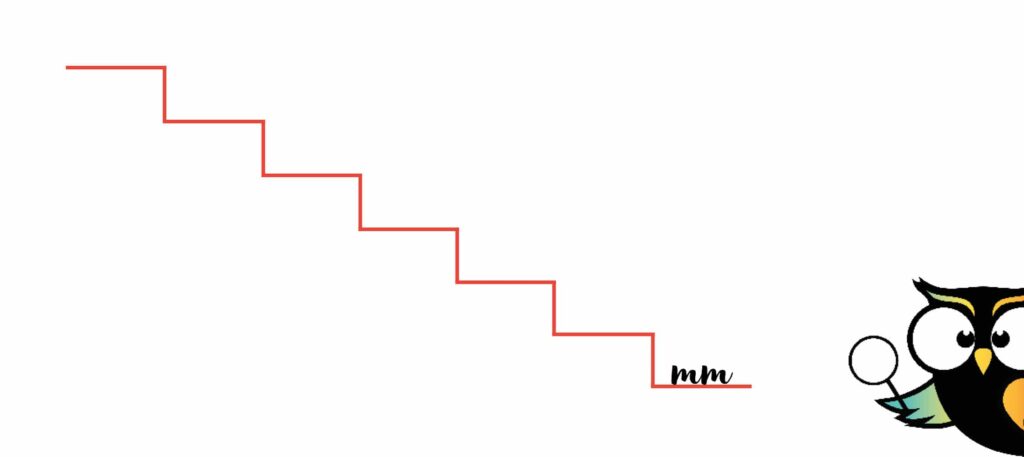
De volgende maateenheid zit ook aan je hand. Dat is namelijk de centimeter. De breedte van je nagel is ongeveer 1 centimeter. Centimeter schrijf je als ‘cm’ en zet je 1 treetje boven de ‘mm’ op de trap.
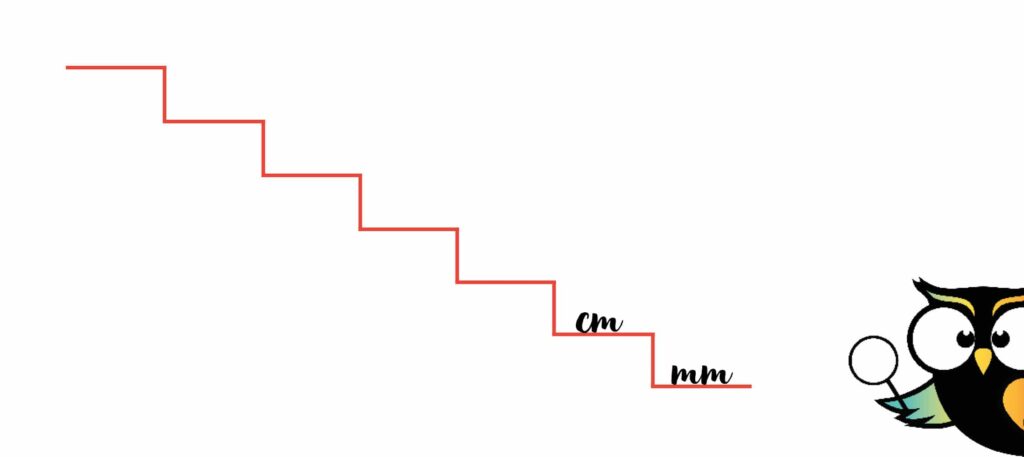
Dan komt de maateenheid decimeter. Ook die heb je altijd bij je. 1 decimeter is de breedte van je hand. Als je je vingers sluit, heb je een decimeter.
Handig hè? Als je het even niet meer weet met die maateenheden, kijk je gewoon naar je handen!
De breedte van een wc-rol is trouwens ook precies 1 decimeter.
Decimeter schrijf je als ‘dm’ en komt 1 trede boven ‘cm’.
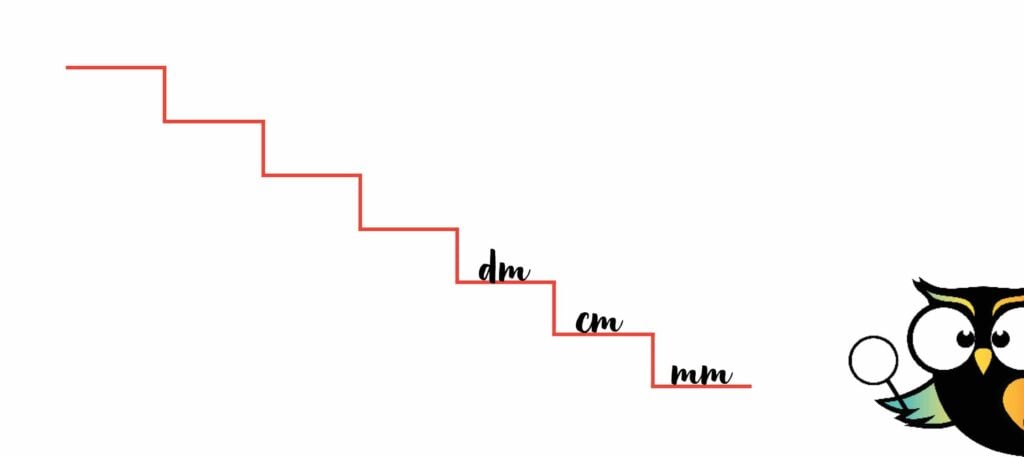
Dan gaan we naar de meter. Een meter heeft jouw leerkracht vast in de klas. Dat is namelijk de grootte van een bordliniaal. Ook een grote stap heeft ongeveer de lengte van een meter.
‘Meter’ korten we op de trap af met alleen de letter ‘m’.
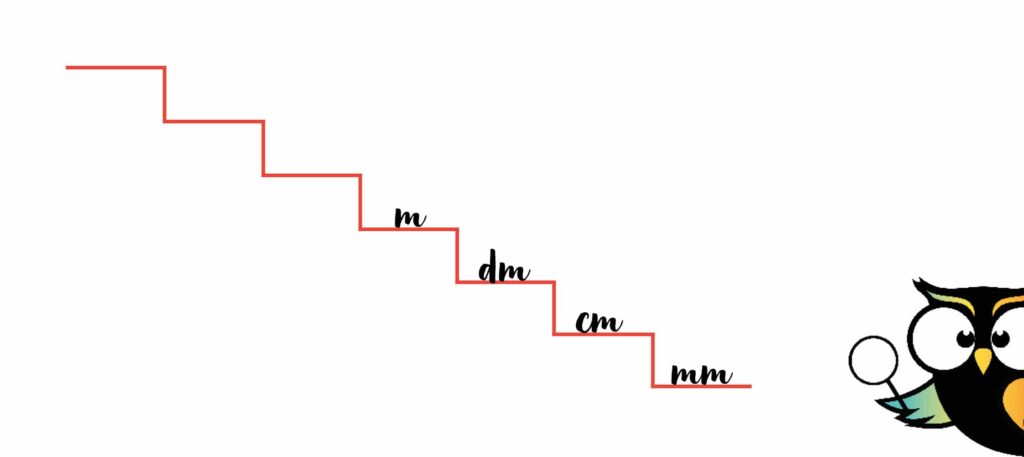
De volgende maateenheid is decameter. Die heb je niet meer aan je lichaam of in de klas. Een decameter is daar te groot voor.
Daarom kijken we nu naar de snelweg. Daar vinden we namelijk de grootste maateenheden.
Een decameter is de afmeting van een vrachtwagen. Decameter schrijf je op de trap als ‘dam’. En je raadt het al: de decameter komt boven de meter op de trap.
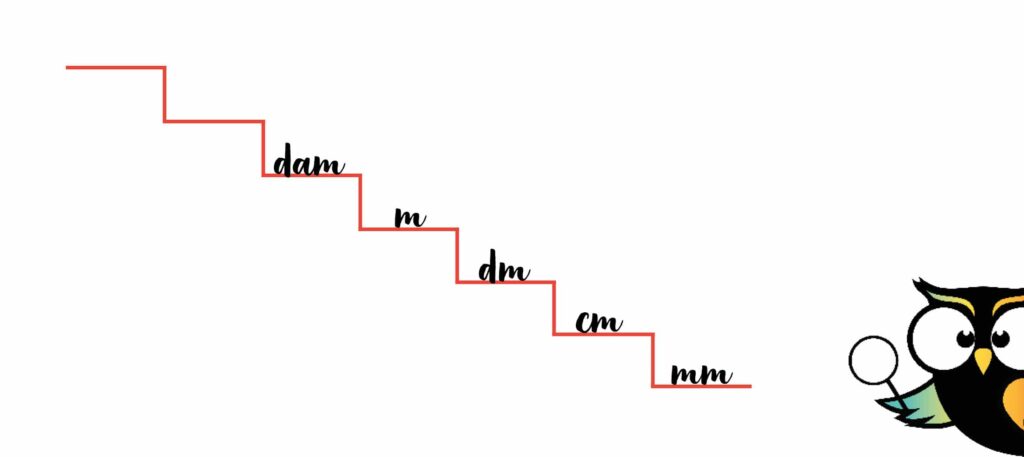
Nu is de hectometer aan de beurt. Ook die vinden we op de snelweg. Heb jij op de snelweg wel eens uit het raam gekeken toen je onderweg was naar je oma of tante? Misschien zijn die groene bordjes in de berm je wel eens opgevallen. Dat zijn hectometerpaaltjes.
Na iedere hectometer staat er weer een nieuw groen paaltje. De afstand tussen deze hectometerpaaltjes is dus een hectometer. Let er maar eens op als je weer op de snelweg komt!
Hectometer schrijven we als ‘hm’ op de trap.
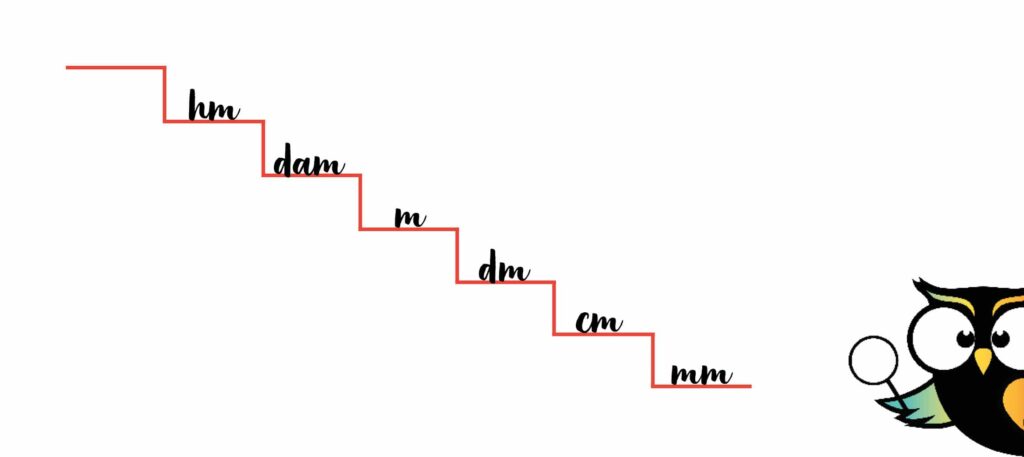
Dan de laatste in deze rij. Dat is de allergrootste: de kilometer. Die komt dan ook bovenaan de trap te staan. Een kilometer is de afstand die een volwassene lopend in ongeveer 12 minuten aflegt.
Kilometer schrijf je op als ‘km’.
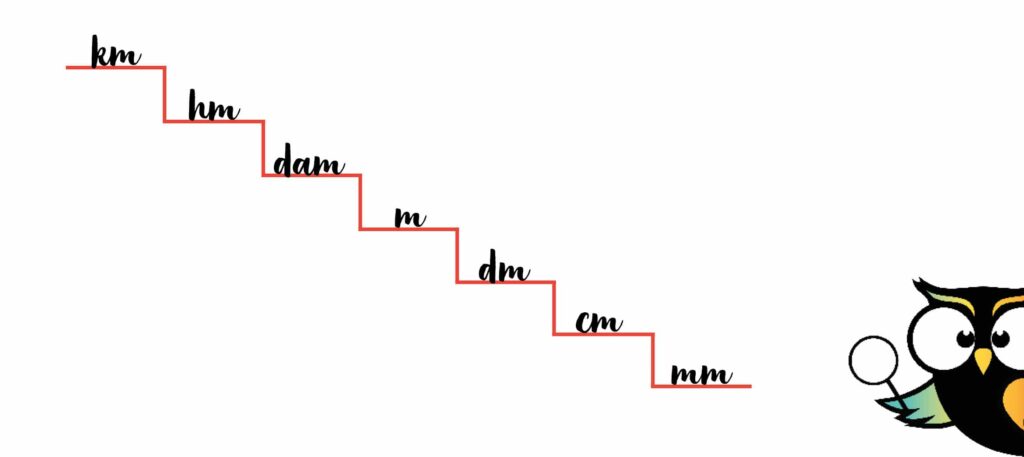
Alle maateenheden staan nu op de trap. Dat is handig, omdat je er straks gemakkelijk mee kunt rekenen.
Je mag er trouwens ook voor kiezen om alle maateenheden naast elkaar te zetten, op een lijn. Dat werkt precies hetzelfde. Het is maar net wat jij gemakkelijk vindt.
Het gaat er wel om dat je de volgorde van de maateenheden goed neerzet. De volgorde is altijd hetzelfde. Van groot naar klein. Links begin je met de grootste maat en rechts eindig je met de kleinste. De andere maateenheden moeten er altijd op dezelfde volgorde tussenin.
Vind je het nog lastig om de juiste volgorde te onthouden? Dan kun je een ezelsbruggetje gebruiken.
Onthoud deze zin en je hebt altijd de volgorde goed:
Kan Het Dametje Met De Centimeter Meten
De eerste letters van deze woorden helpen je de goede volgorde te bepalen:
- Kan = kilometer (km)
- Het = hectometer (hm)
- Dametje = decameter (dam)
- Met = meter (m)
- De = decimeter (dm)
- Centimeter = centimeter (cm)
- Meten = millimeter (mm)
Met deze zin weet je zeker dat je de maateenheden goed op de lijn hebt staan.
Hoe werkt het metriek stelsel?
De volgende stap is dat je weet wat er met de getallen gebeurt als je van de ene maat naar de andere maat gaat (maten omrekenen).
Als je op een liniaal kijkt, zie je de centimeters staan. Maar als je heel goed kijkt, zie je tussen de centimeters nog meer heel kleine streepjes staan. Dat zijn de millimeters. Als je ze telt, zie je dat er 10 millimeters zitten in 1 centimeter. Dat is goed om te weten.
1 cm is dus hetzelfde als 10 mm. Dat betekent dat je, als je een stap naar rechts doet op de trap, je het getal keer 10 doet. Dat geldt niet alleen voor de stap van centimeter naar millimeter, maar voor iedere stap. Daarom staat er vanaf nu een pijl boven de tredes met ‘keer 10’.
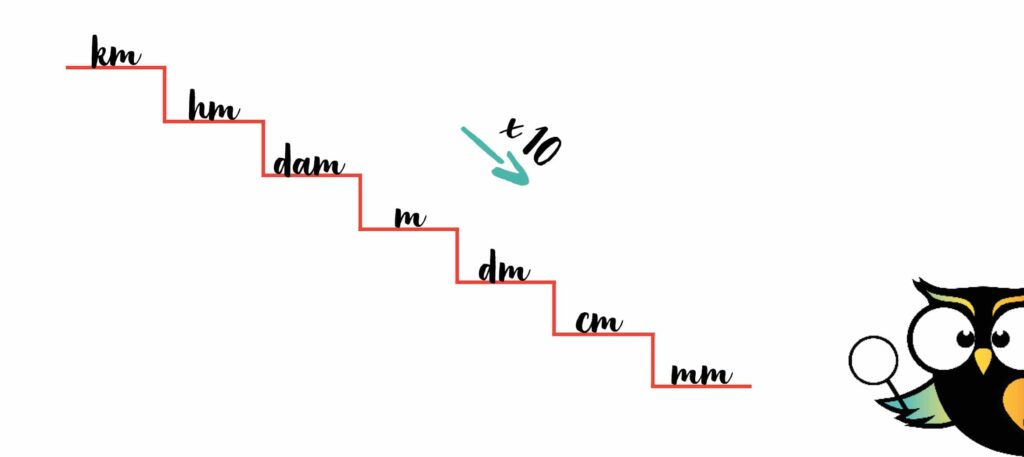
Bij elke stap die je naar rechts zet, wordt je getal dus 10 keer groter. Als je bijvoorbeeld 1 meter hebt, is dat hetzelfde als 1 x 10 = 10 decimeter.
Andersom werkt het ook. Als je naar links gaat, dus van millimeters naar centimeters, wordt het getal steeds 10 keer zo klein. 10 millimeter is bijvoorbeeld 1 centimeter.
Je hebt het getal van de millimeters daarvoor door 10 gedeeld. Dat betekent dat je onderlangs een pijl tussen iedere 2 treden kunt zetten met ‘gedeeld door 10’.
Zo dus:
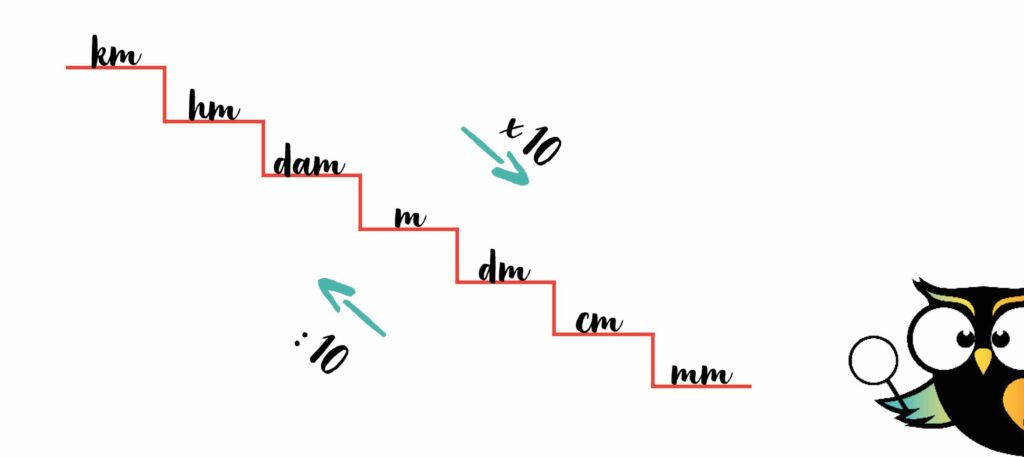
Ook hier geldt dezelfde regel voor ieder stapje.
We kunnen deze informatie heel mooi samenvatten (mét handig ezelsbruggetje!):
- Als je naar rrrrrrechts gaat, doe je keerrrrr 10.
- Als je naar lllllllinks gaat, deelllllll je door 10.
Maar wanneer heb je deze informatie dan nodig? Je gebruikt hem wanneer je maateenheden wilt omrekenen.
Stel je voor dat jij een muur van je slaapkamer wilt behangen. Je meet dan de muur op, om te zien hoeveel behang je moet kopen. De muur is bijvoorbeeld 400 cm. In de winkel staat op de rollen behang alleen niet hoeveel centimeter een rol is, maar hoeveel meter.
Dan is het wel handig dat jij weet hoe je dit kunt omrekenen.
Je wilt dus het volgende weten:
400 cm = … m
Pak nu de trap erbij.

Je weet dat de muur 400 cm is. Van centimeter moet je naar meter. Dat betekent dat je naar links moet werken. En weet je nog? Naar links is delen door 10 bij ieder stapje.
Eerst ga je van cm naar dm.
400 : 10 = 40
Je weet nu dus dat 400 cm hetzelfde is als 40 dm.
Nu doe je nog een stapje naar links; van dm naar m.
40 : 10 = 4
Nu weet je ook dat 40 dm (en dus 400 cm!) gelijk is aan 4 m!
Je muur was 400cm en dat is dus hetzelfde als 4 meter.
Je kent nu het metriek stelsel van de meters helemaal. Ook weet je hoe je het moet gebruiken in je rekensommen. Het is nu niet meer zo moeilijk om ook andere metrieke stelsels te maken, zoals die van de grammen en de liters. Ze lijken namelijk enorm veel op elkaar.
Metriek stelsel gram
Grammen gebruiken we om aan te geven hoe zwaar iets is. Ook de verschillende maateenheden van de grammen kun je op een metriek stelsel plaatsen.
Laten we eerst nog eens kijken naar het metriek stelsel van de meters.

We beginnen nu bij de basis en vervangen ‘meter’ door ‘gram’.
En eigenlijk is dat alles wat je hoeft te doen. Op elke trede vervang je ‘meter’ door ‘gram’ en je hebt het metriek stelsel van de grammen!

De grootste maat is dus geen kilometer, maar een kilogram.
De kleinste maat is milligram in plaats van millimeter.
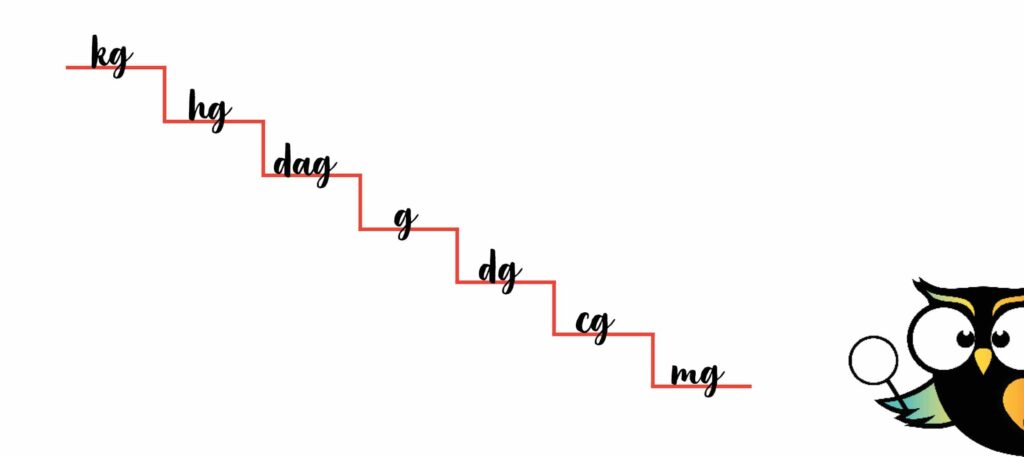
En zo doe je dat ook voor de rest van de trap. Alle m’s vervang je door g’s. Niet zo moeilijk, toch?
Het metriek stelsel van de grammen werkt precies hetzelfde als dat van de meters. Naar rechts is keer 10 en naar links is gedeeld door 10.
Metriek stelsel liter
Het zal je misschien niet verbazen dat we hetzelfde trucje kunnen gebruiken als we het metriek stelsel van de liters willen maken.
Liters geven aan welke hoeveelheid ergens in past. Bijvoorbeeld hoeveel water er in de vijver in de tuin zit. Ook in recepten kom je vaak een maateenheid van liters tegen. Zo staat in een recept voor cake bijvoorbeeld beschreven hoeveel milliliter melk je nodig hebt.
Nu we weten dat het metriek stelsel van de liters hetzelfde werkt als dat van de meters en de grammen, is het niet zo moeilijk meer om dat stelsel te maken.
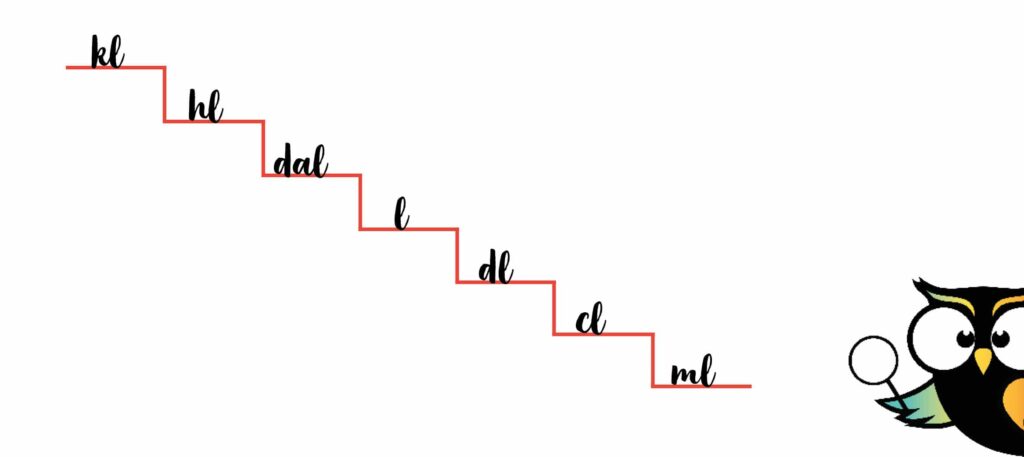
Kilometer (km) wordt kiloliter (kl), millimeter (mm) wordt milliliter (ml) enzovoort. Ook de rekenstappen zijn in dit stelsel precies hetzelfde.
Nu gaan we het een stapje moeilijker maken. We gaan kijken naar het metriek stelsel van oppervlakte en inhoud.
Metriek stelsel voor oppervlakte en inhoud
Het metriek stelsel kun je nog uitbreiden door ook de oppervlaktematen en de inhoudsmaten om te rekenen.
Voordat we dat gaan doen, vertellen we hier nog even kort hoe het ook alweer zat met oppervlakte en inhoud:
- De oppervlakte geeft aan hoe groot een vlak is, bijvoorbeeld de tuin. Je geeft de oppervlakte altijd aan in vierkante meters, vierkante centimeters enzovoort. De afkortingen die je gebruikt, krijgen zo’n klein 2’tje boven de laatste letter: m², cm², km².
- De inhoud geeft aan welke hoeveelheid er in iets past, bijvoorbeeld hoeveel zand er in de zandbak past. Dat geef je aan in liters of in kubieke meters, kubieke decimeters enzovoort. Deze afkortingen krijgen een klein 3’tje boven de laatste letter: m³, dm³.
Voor liters gebruik je het metriek stelsel dat we hierboven hebben gemaakt. Voor kubieke meters moet je een nieuwe maken.
De trappen voor de oppervlakte en inhoud zien er eigenlijk hetzelfde uit als alle andere. Kijk maar:
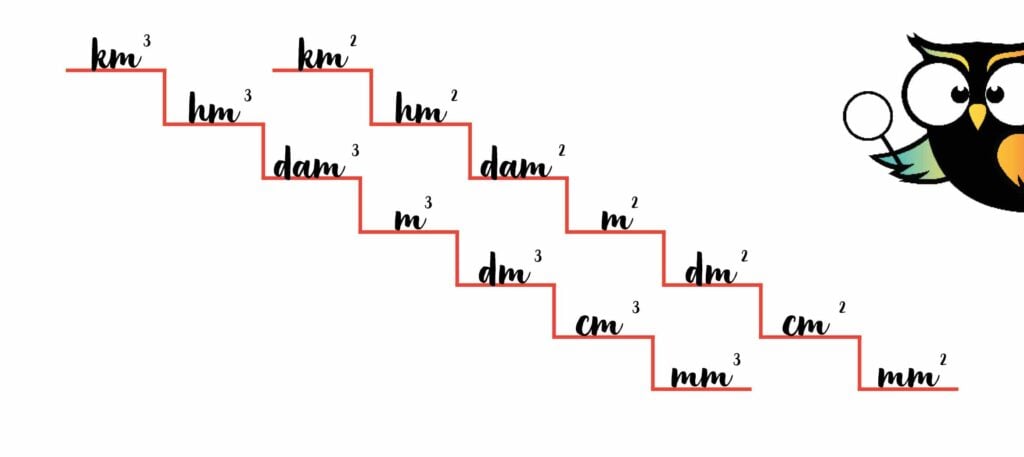
Er is alleen één heel groot verschil!
Als je nu gaat omrekenen werk je niet met ‘keer 10’ of ‘delen door 10’. Bij de oppervlaktes werk je met ‘keer 100’ of ‘delen door 100’.
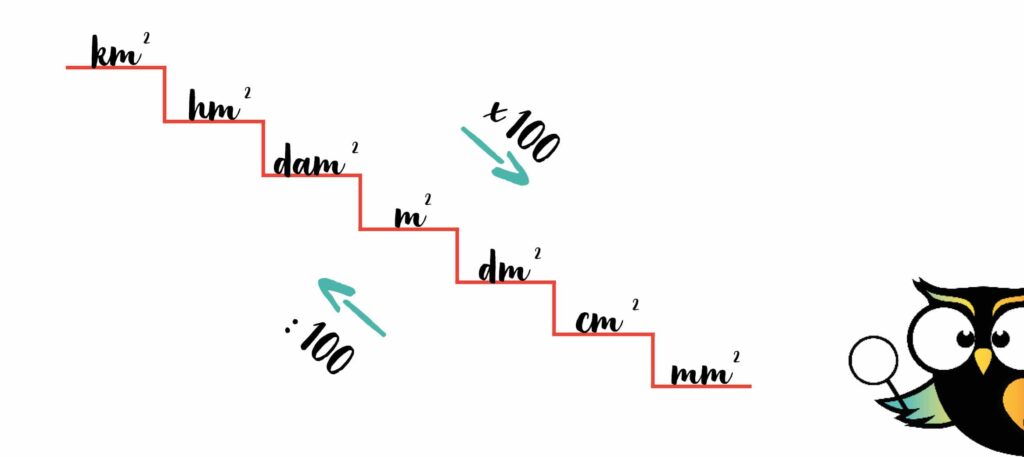
En bij de inhoud werk je met ‘keer 1000’ of ‘delen door 1000’.
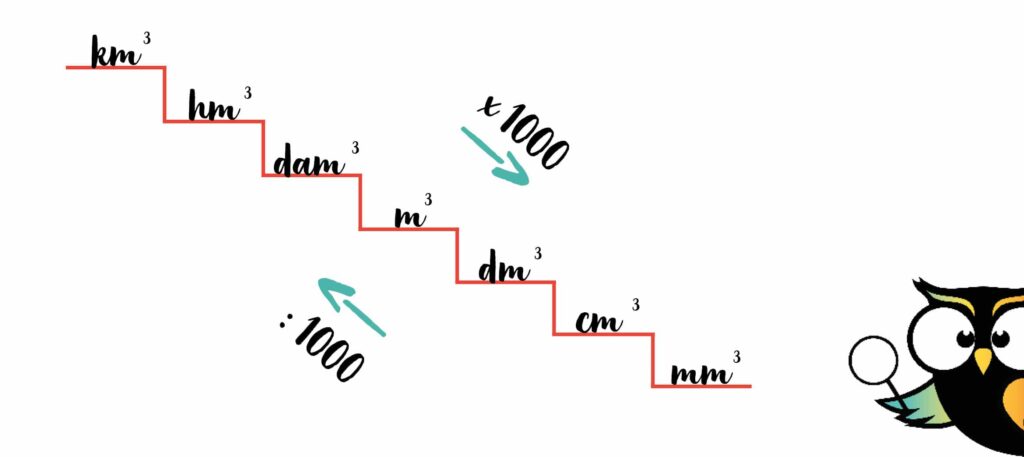
Je kunt deze getallen gemakkelijk onthouden. Er is namelijk een ezelsbruggetje voor!
Bij de oppervlaktematen zie je steeds dat kleine 2’tje boven de afkorting. Dat zijn dan de 2 nullen van de 100.
En bij inhoud staat een klein 3’tje. Je raadt het al: dat zijn dan de 3 nullen van de 1000.
Verder werken deze stelsels precies zoals je het gewend bent van de meters, de grammen en de liters.
Je kunt nu de maten omrekenen met behulp van het metriek stelsel!
Metriek stelsel werkbladen
Nu je alles weet over het metriek stelsel en weet hoe je het kunt gebruiken om maateenheden om te rekenen, is het tijd om te oefenen.
Hieronder vind je een aantal sommen op een werkblad. De antwoorden vind je helemaal onderaan. Ga er lekker mee aan de slag. Dan weet jij straks hoe goed je de inhoud van dit artikel hebt begrepen.
Vind je het nog moeilijk? Zoek dan nog eens op in de tekst hoe het ook alweer zit. Vraag desnoods iemand om hulp.
Opdracht 1
- Wat moet je doen als je bij het stelsel van de meters een stapje naar rechts gaat?
- Wat staat er in het stelsel van de grammen rechts van kilogram?
- Vul het stelsel van de liters helemaal in
- Wat moet je doen als je in het stelsel van de oppervlakte een stapje naar links gaat?
Opdracht 2
Vul in:
- 30 dm = __ m
- 2 km = __ dam
- 450 mm = __ cm
- 500 cm = __ m
- 3 dam = __ cm
Opdracht 3
Vul in:
- 1 l = __ dl
- 30 mg = __ cg
- 20 kl = __ hl
- 500 dm = __ dam
- 3000 cg = __ dag
Opdracht 4
Vul in:
- 30 m² = __ dm²
- 2000 mm³ = __ cm³
- 400 hm² = __ km²
- 3.000.000 cm³ = __ m³
- 8 km² = __ m²
Opdracht 5
- 5 g = __ mg
- 70 ml = __ cl
- 6 km² = __ hm²
- 20.000 mm³ = __ cm³
- 400 km = __ dam
Antwoorden opdracht 1
- Dan doe je het getal x 10.
- Rechts van kilogram staat hectogram
- Van links naar rechts: kl, hl, dal, l, dl, cl, ml
- Dan deel je het getal door 100.
Antwoorden opdracht 2
- 30 dm = 3 m
- 2 km = 200 dam
- 450 mm = 45 cm
- 500 cm = 5 m
- 3 dam = 3000 cm
Antwoorden opdracht 3
- 1 l = 10 dl
- 30 mg = 3 cg
- 20 kl = 200 hl
- 500 dm = 5 dam
- 3000 cg = 3 dag
Antwoorden opdracht 4
- 30 m² = 3.000 dm²
- 2000 mm³ = 2 cm³
- 400 hm² = 4 km²
- 3.000.000 cm³ = 3 m³
- 8 km² = 8.000.000 m²
Antwoorden opdracht 5
- 5 g = 5000 mg
- 70 ml = 7 cl
- 6 km² = 600 hm²
- 20.000 mm³ = 20 cm³
- 400 km = 40 000 dam
Bekijk ook:

Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 5 (Gratis)

Oefenbladen Rekenen Groep 6 (Gratis)





Top !!!
Prima uitleg hoor toppie mijn leerlingen hebben er heel veel deugd aan !