
Het leren vermenigvuldigen is geen gemakkelijke klus. Veel kinderen hebben er moeite mee. De rekenmethodes starten in groep 4 met het aanleren van de tafels zoals wij die kennen: de rijtjes worden opgedreund. De tafels spelen bij het oefenen van rekenen een belangrijke rol.
Bekijk ook:
- Tafels van vermenigvuldiging Rekenbox (aanbevolen door onderwijsexperts)
- Tafels oefenen groep 4
- Tafels leren groep 4
- Tafels oefenen groep 5
- Print ook de handige tafelkaarten hier!
De tafels leren
De ene methode houdt het bij het rekenen in groep 4 bij de tafels 1 tot en met 5 en de tafel van 10. De andere methode leert meteen alle tafels tot en met 10 aan. Maar voordat je kind de tafels leert, is er al heel wat voorbereidend werk aan vooraf gegaan.
-
Klokkijken Groep 4/5 oefenboek + videobijles
Oorspronkelijke prijs was: 49,90.39,90Huidige prijs is: 39,90. BundelkortingIn mijn winkelwagen Bekijk detailsRekenpakket Groep 4 – 2e helft schooljaar (Cito-IEP)
Oorspronkelijke prijs was: 59,90.54,00Huidige prijs is: 54,00. BundelkortingIn mijn winkelwagen Bekijk detailsHet begint al in groep 1. Jonge kinderen leren vooral door dingen te dóen. De juf geeft aan 3 kinderen 2 gekleurde potloden. Ze vraagt aan haar leerlingen hoeveel potloden de kinderen hebben. Hoogstwaarschijnlijk worden de potloden 1 voor 1 geteld.
Jaren later rekent je kind de som 3 x 2 = 6 moeiteloos uit. Maar voordat het zover is, moet er nog heel wat gebeuren.
Groepjes maken van voorwerpen
In de onderbouw is je kind vooral met materiaal bezig. Door veel te doen ervaart hij de eigenschappen van materialen, ontdekt hij wat hij ermee kan doen en breidt hij zijn kennis uit.
Je kind leert dat hij groepjes kan maken van voorwerpen en ze bij elkaar kan optellen.
Dit wordt eindeloos gevarieerd en herhaald. In groep 2 telt je kind tot 20 en kan hij dus ook een vermenigvuldigsom tot 20 oplossen.
Het aanleren van het vermenigvuldigen verloopt nog niet erg gestructureerd. Af en toe wordt de lesstof in de kring aangeboden. Afhankelijk van de vaardigheden van je kind zal de leerkracht hem daarnaast passende opdrachtjes geven.
De tafels leren: de voorbereiding in groep 3
In groep 3 komt er meer structuur in het aanleren van het vermenigvuldigen. Er wordt toegewerkt naar het daadwerkelijk aanleren van de tafels in groep 4. Je kind begint met materiaal, zodat hij ziet wat er gebeurt. Een belangrijke stap daarna is het benoemen wat hij ziet. Hij leert het begrip ‘keer’ zonder dat hij het symbool (x) daarvoor gebruikt.
Voor veel kinderen is het benoemen van wat ze zien geen vanzelfsprekendheid. Voor het verdere leerproces is het belangrijk dat je kind de zogenaamde vermenigvuldigtaal begrijpt en kan verwoorden.
Juf zegt: “Ik geef John, Marieke, Roos en Jelte ieder 2 potloden. Hoeveel potloden heb ik uitgedeeld? Ik tel alle potloden bij elkaar op. Ik heb 8 potloden uitgedeeld.”
Een mooi rekenmomentje
De leerkracht zal in het begin alle potloden 1 voor 1 tellen en waarschijnlijk zal er een slimmerik zijn die zegt dat dit veel sneller kan. En dat is wat ik een mooi rekenmomentje noem.
Rekenen is namelijk zo snel mogelijk tot een goede oplossing komen. En herhaald optellen betekent een belangrijke versnelling in het rekenproces. De slimmerik heeft een patroon ontdekt waardoor hij niet steeds alle potloden meer stuk voor stuk hoeft te tellen.
Nu het herhaald optellen wordt herkend, kan het worden toegepast. En tot slot verandert het verhaaltje van de potloden in een som:
4 keer 2 is 8
In groep 3 leren de kinderen deze taal aan. Het symbool dat hierbij hoort, x, leren ze later. Vervolgens wordt het concrete materiaal vervangen voor tekeningen in een werkboek. En die tekeningen worden weer vervangen voor symbolen. Zo worden de sommen steeds abstracter.
De tafels aanleren op 3 manieren
Er worden 3 modellen aangeboden om het vermenigvuldigen inzichtelijker te maken:
- het rechthoekmodel
- het groepjesmodel
- het lijnmodel
Het rechthoekmodel
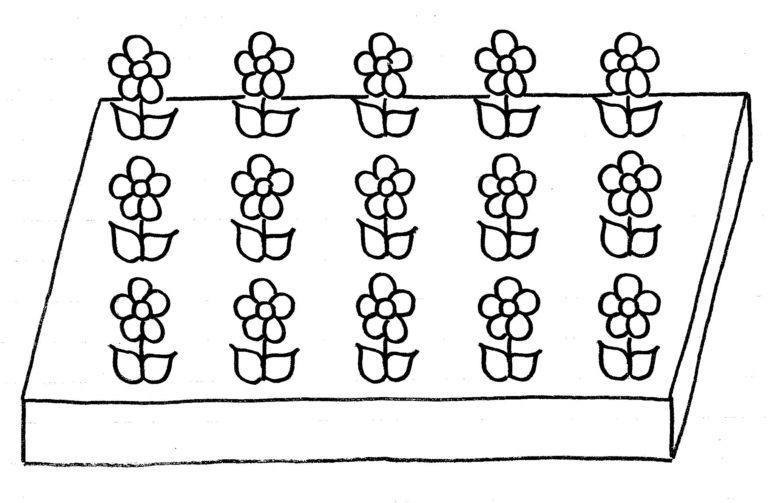
Een voorbeeld van een rechthoekmodel is een bak met zomerplantjes.
De bak is 3 rijen breed en 5 rijen lang.De structuur van de bak – de plantjes staan netjes op een rij – nodigt uit tot versneld optellen. Namelijk 5 + 5 + 5. Dit model staat getekend in het werkboek op school, met mooie plantjes erin, zodat je kind zich er een goede voorstelling van kan maken.
Een volgende stap is het zelf tekenen van het model. Dan zullen de plantjes al vrij snel veranderen in symbolen. De versnelling in het rekenproces zal hierdoor vanzelf ontstaan.
Het groepjesmodel
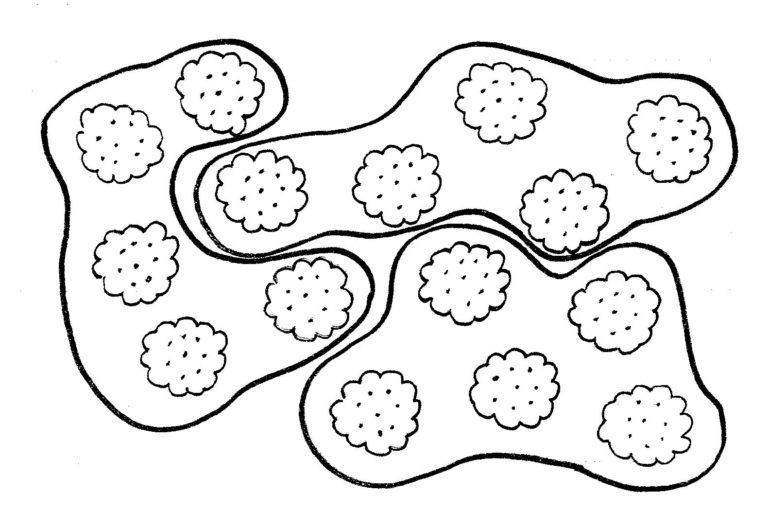
Een ander model is het groepjesmodel.
“Maak groepjes van 5 koekjes en tel hoeveel groepjes je hebt getekend.”
Je kunt deze opdracht ook eerst concreet voordoen en daarna kan je je kind een vergelijkbare opdracht laten maken.
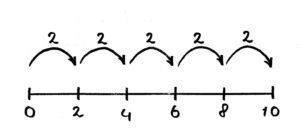
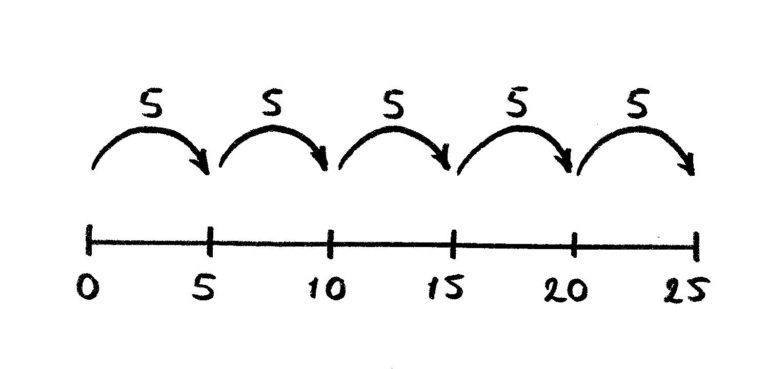
Het lijnmodel
Tot slot het lijnmodel. Bij dit model wordt gebruik gemaakt van een getallenlijn. Op deze lijn laat je sprongen zien. Het herhaald optellen wordt zo heel inzichtelijk gemaakt.
In deze 3 modellen is er sprake van voorbereidend vermenigvuldigen. Je kind ziet wat er gebeurt, maar maakt nog geen gebruik van van formele taal. Het woord ‘keer’ blijft nog achterwege. Het leren verwoorden en handelen vindt tegelijkertijd plaats, zodat je kind een koppeling leert maken tussen wat hij zegt en doet. Zo blijft de taal betekenisvol.
Je kind leert eerst wat vermenigvuldigen inhoudt en dan pas hoe je de som noteert.
De tafelsommen sneller oplossen
Nu je kind weet wat vermenigvuldigen inhoudt, kan hij verder naar de volgende stap. Hij mag nu zelf een betekenisvolle situatie bedenken bij de opgegeven som. Op deze manier blijft de keersom betekenis houden en weet je kind wat hij doet.
In deze begripsvormingsfase krijgen de rechthoek- en groepsmodellen veel aandacht. Deze modellen zorgen ervoor dat je kind begrijpt wat hij doet. Deze ondersteunende modellen verklaren dat het bij vermenigvuldigen gaat om herhaald optellen.
Een groot nadeel van het rijtjesmodel is dat je kind de neiging kan krijgen om alles te tellen. Je kind ziet bijvoorbeeld 3 dozen staan met 4 sinaasappelen en gaat alle sinaasappelen tellen.
Natuurlijk zijn er kinderen die het tellen snel beu worden en uit zichzelf een verkorte strategie bedenken, maar dat is niet bij de meerderheid het geval. De meeste kinderen moeten de juiste strategie bewust aanleren.
Om het versneld optellen te stimuleren is er een oplossing bedacht. De dozen sinaasappelen worden gestapeld en alleen in de bovenste doos kun je het aantal sinaasappelen zien.
Als er in de bovenste doos 6 sinaasappelen liggen, dan zitten die ook in de andere dozen. Je kind kan ze niet meer tellen en moet nu de som 6 + 6 + 6 = uitrekenen. Dit is al een behoorlijke versnelling ten opzichte van het 1 voor 1 tellen. Aanvankelijk stond het aanleren van de strategie centraal en nu wordt het benoemen van het juiste antwoord steeds belangrijker.
Makkelijk tafels leren: veel gebruikte strategieën
Nu je kind weet wat vermenigvuldigen inhoudt, leert hij hoe hij de vermenigvuldigsommen sneller kan oplossen. Je kind leert:
- de omkeerstrategie (8 x 4 = 4 x 8)
- verdubbelen (3 x 4 = 12 dus 6 x 4 = het dubbele van 12)
- halveren (10 x 4= 40, 5 x 4 = 20, de helft van 40)
De omkeerstrategie blijkt het meest eenvoudig te zijn. De andere 2 vragen om meer rekenkundig inzicht. Je kind is bij die strategieën tegelijkertijd hard bezig met automatiseren van het optellen en aftrekken. Daarom zijn deze 2 strategieën lastiger. Het is echter wél belangrijk dat je kind leert dat er verschillende mogelijkheden zijn om de som op te lossen. Een goede rekenaar beschikt namelijk over verschillende oplossingsstrategieën.
Tafels oefenen groep 4
Je hebt hierboven gelezen wat er allemaal bij komt kijken als je kind de tafels gaat leren. In groep 4 is het dan zo ver. Het aanleren van de tafel van 1 levert nooit problemen op. De tafel van 0 zorgde altijd voor hilariteit bij mijn leerlingen.
De tafels van 2 en 10 worden daarna als eerste aangeleerd. Bij de tafel van 2 worden alle even getallen opgenoemd. Dit hebben ze in groep 2 al geleerd. Het blijft wel belangrijk om er een betekenis aan te koppelen.
Je kunt bijvoorbeeld schoenparen tellen.
Ook blijkt dat het aanleren van de tafel van 5 eenvoudig is. Ter ondersteuning kun je handen gebruiken. Die maken het erg gemakkelijk om deze tafel aan te leren.
Nu de tafels van 2, 5 en 10 geleerd zijn, volgen de tafels van 3 en 4. Een aantal sommen is al bekend, omdat ze in de al aangeleerde tafels voorkomen. Je kind heeft inmiddels de omkeerstrategie geleerd, dus voor hem zal 3 x 2 hetzelfde zijn als 2 x 3. Naast de omkeerstrategie gebruikt je kind ook de tafels door te verdubbelen en herhaald optellen.
Als steunpunt worden de sommen 5x .. en 10x… gebruikt. Het is belangrijk dat je kind niet te lang blijft hangen in het herhaald optellen, omdat dit foute antwoorden in de hand werkt.
Automatiseren van de tafels
Nu je kind kennis heeft gemaakt met de eerste tafels, wordt het tijd voor het automatiseren en vervolgens het memoriseren.
Bij automatiseren gaat het erom dat je kind binnen 10 seconden het goede antwoord weet. Hij mag eventueel gebruik maken van een tussenstapje. Hij is nog heel even aan het rekenen voordat hij het antwoord weet. Bij memoriseren wéét je kind het antwoord en zegt dit vlot en goed. Dit is het einddoel van het aanleren van de tafels.
Helaas halen veel kinderen dit doel niet, maar de leerkracht is al erg blij als je kind de tafels geautomatiseerd heeft. Je kind redt zich daarmee prima in zijn verdere leerproces. Het automatiseren wordt geleerd door sommen niet meer op volgorde te oefenen, maar door elkaar.
Natuurlijk komt het nog voor dat de hele tafelrij wordt opgezegd, maar dit gebeurt steeds minder vaak. Je kind kan nog wel gebruik maken van strategieën, maar het accent ligt in deze fase op het toepassen van handig rekenen.
Welke hulpsom is het handigst bij deze opgave?
Je kind leert hier flexibel mee om te gaan, zodat hij vlot en goed de som kan uitrekenen. En hoe meer sommen je kind uit het hoofd weet, des te meer steunpunten heeft hij.
Tafels oefenen groep 4 werkbladen
Download de gratis oefenbladen rekenen voor het oefenen van sommen voor groep 4 (of voor andere groepen).
OefenbladOefenbladen Rekenen Groep 4 (Gratis)
OefenbladOefenbladen Rekenen Groep 5 (Gratis)
Specifiek voor het oefenen van de tafels is het Oefenboek Tafels beschikbaar.
Tafel van 6-7-8-9 oefenen
Na de tafels 2 tot en met 5 en 10 komen de tafels 6 tot en met 9 aan bod. Het automatiseren van de eerder geleerde tafels gaat ondertussen gestaag door. Het aanleren van de ‘hogere’ tafels is voor veel kinderen moeilijk. De tafel van 5 gaat nog wel, maar dan…
De leerkracht maakt gebruik van bestaande kennis. Strategieën als omkeren, verdubbelen, 1 x meer of minder worden volop gebruikt. Daarnaast werkt het goed als een opgave getekend wordt, het alom bekende rijtjesmodel wordt hier veelvuldig gebruikt.
Het blijft belangrijk dat er een betekenis wordt gekoppeld aan de opgave. Dit helpt bij het onthouden en je kind begrijpt wat hij doet. Ook leert je kind dat de hogere tafel niet helemaal nieuw is.
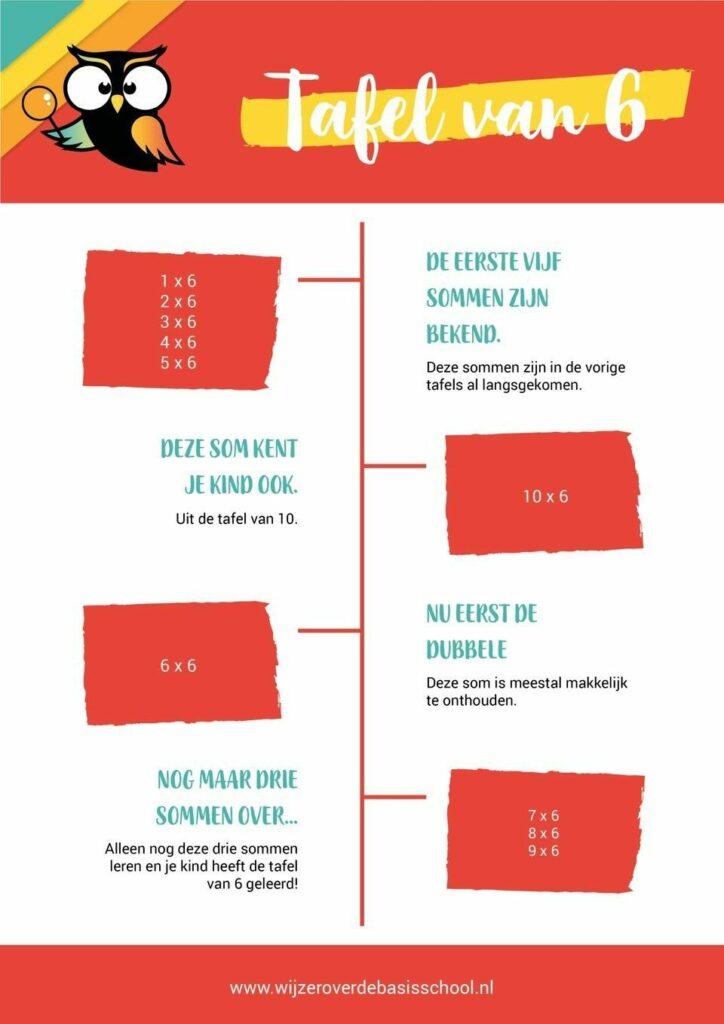
Neem de tafel van 6. De eerste 5 sommen zijn bekend, omdat deze in de vorige tafels al langskwamen. En 10 x 6 kent je kind ook. Dan hoeft hij nog maar 4 sommen te leren. 6 x 6 is een dubbele en die weet hij vast wel. Dan blijven er nog 3 sommen over. Dat valt nog te overzien.Tafels oefenen groep 5
In de loop van groep 5 bekijk ik vaak welke sommen de kinderen beheersen. Alle sommen staan in een schema. Vervolgens gebruik ik dit stappenplan:
- Ik kleur alle goede antwoorden groen.
- Alle foute antwoorden krijgen een rode kleur.
- Twijfelachtige antwoorden worden oranje gekleurd.
Meestal blijkt dat een kind de meeste sommen wel beheerst. Als je kind ziet hoeveel sommen hij wel beheerst, is dat een enorme stimulans om de rest van de sommen ook te leren.
Je kind denkt dat hij de tafels helemaal niet kan, maar eigenlijk valt het meestal wel mee. Een paar sommen moet hij nog oefenen en dat is nog te overzien. De meeste kinderen kennen, na gericht oefenen, na een week ook de meest lastige keersommen uit hun hoofd.
Grote keersommen oefenen
Nu je kind alle tafelsommen tot en met 10 heeft geleerd, kan hij ook sommen als 14 x 6 = uitrekenen. Je kind splitst 14 in de getallen 10 en 4. Dan maakt hij 2 keersommen: 10 x 6 = en 4 x 6 =.
Deze sommen kan hij eenvoudig uitrekenen. De uitkomsten telt hij bij elkaar op. Door het hoge getal te splitsen wordt het rekenen met hogere getallen eenvoudiger.Tafels oefenen op papier en nog 7 andere manieren
De laatste jaren is er veel te doen geweest over het aanleren van de tafels. Jarenlang is hier te weinig aandacht aan besteed in het onderwijs. Een kind leerde de tafels, maar van herhaling was geen sprake. Hier zijn ze gelukkig van teruggekomen, want uit veel onderzoeken blijkt dat je de tafels vaak moet herhalen, ook in de groepen 7 en 8. Dat kan op verschillende manieren.
Het meest efficiënt blijkt het mondeling oefenen; het ouderwetse rijtjes dreunen. Ik denk dat dit inderdaad zo is. Deze methode is goed te gebruiken naast de reguliere lesmethoden. Je kind moet op een gegeven moment wel weten wat vermenigvuldigen inhoudt. Daar wordt immers veel aandacht aan besteed in de rekenmethoden. Het inoefenen van de tafels komt veel minder aan bod. Het is aan de leerkracht hoeveel tijd hij hierin wil steken.
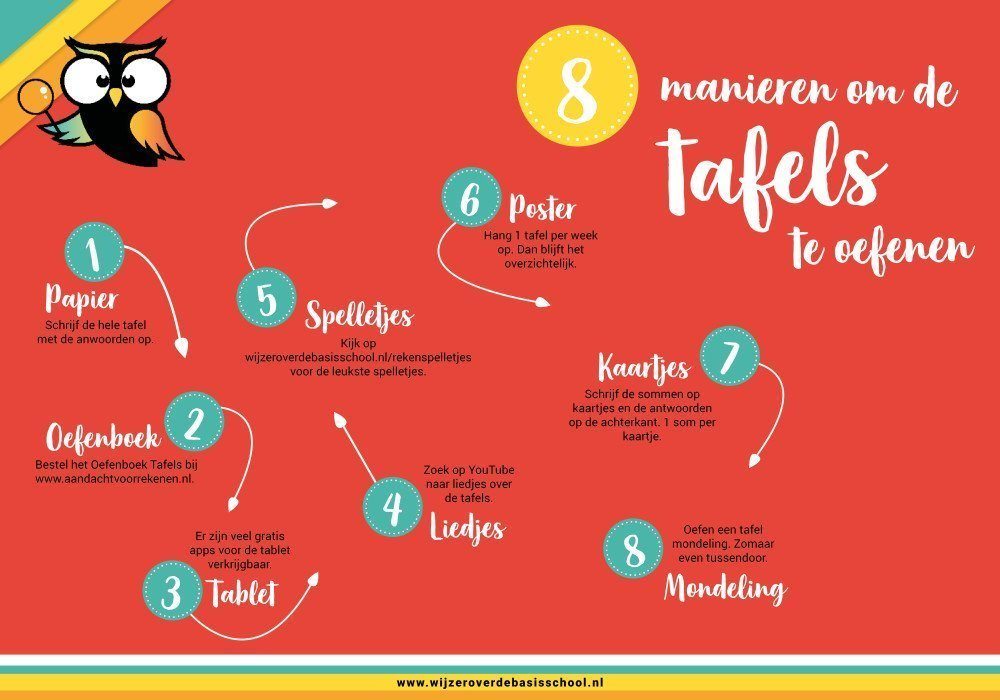
Andere manieren van inprenting
Voor het inprenten van de antwoorden zijn vele oefenmogelijkheden die je heel goed ook thuis kunt gebruiken. In onderstaand overzicht vind je een aantal opties.
Je ziet dat het aanleren van tafels een heel proces is dat al in de onderbouw start. Je kind leert eerst spelenderwijs wat herhaald optellen is. Langzamerhand wordt er toegewerkt naar het aanleren van de befaamde rijtjes. Belangrijk hierin is het herhalen. Hoe vaker, hoe beter. En juist dat herhalen kunnen jullie thuis heel goed doen. Bedenk: hoe eerder je kind de tafels kent, hoe gemakkelijker hij het heeft in de rekenles.
Bekijk nu hieronder de leuke spelletjes die je thuis kunt doen om de tafels te oefenen.Tafels oefenen groep 4 spelletjes
Hieronder vind je leuke en leerzame spelletjes die je thuis kunt doen om de tafels te oefenen. Elk spelletje wordt uitgelegd in een video en eronder staat een link naar het materiaal dat je erbij nodig hebt. Het materiaal kun je gratis downloaden.
4 op een rij met tafels
Wat heb je nodig?
- een 4-op-een-rij-kaart
- 2 kleuren fiches
- 2 pionnetjes (of 2 paperclips, 2 bonen of 2 …)
- een dobbelsteen
Download de 4-op-een-rij-kaart
Hoe speel je het spel?
- Print de 4-op-een-rij-kaart.
- Verdeel de fiches.
- Gooi nu allebei met de dobbelsteen.
- Wie het hoogste heeft gegooid, mag de pionnetjes onder 2 getallen zetten en beginnen:
- Kies 2 getallen in de rij onder de 4-op-een-rij-kaart en zet onder beide getallen een pionnetje.
- Maak nu een keersom van de 2 getallen. Leg een fiche op het goede antwoord. Bijvoorbeeld: 1 pionnetje onder 4 en 1 pionnetje onder 6:
4 x 6 = 24. Leg het fiche op het getal 24.
- De beurt gaat nu naar de andere speler. Die zet 1 van de pionnetjes onder een ander getal, maakt een keersom van de 2 getallen waar de pionnetjes onder staan en legt zijn fiche op het goede antwoord.
Bijvoorbeeld: verplaats het pionnetje dat onder 4 staat naar 7: 7 x 6 = 42. Leg het fiche op het getal 42. - De beurt gaat weer naar de andere speler. Die zet 1 van de pionnetjes onder een ander getal, maakt een keersom van de 2 getallen waar de pionnetjes onder staan en legt zijn fiche op het goede antwoord.
- Enzovoort.
Wie het eerst 4 op een rij heeft, heeft gewonnen!
Tafels oefenen met tafelbingo
Download de instructie van Tafelbingo (+ extra spelvariant)
Met hoeveel personen speel je dit spel?
- Met 2 of meer personen
Wat heb je nodig?
- lege bingokaarten
- een tafelkaart
- 2 dobbelstenen
- voor iedereen een pen of potlood
Hoe speel je dit speel?
- Maak voor iedereen die meedoet een bingokaart.
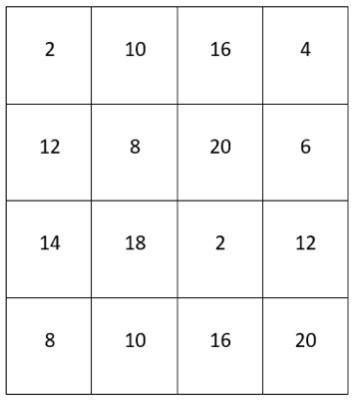
- Vul op de lege bingokaarten antwoorden in van de tafels van 1 tot en met 6 (alle antwoorden vind je op de tafelkaart). Zorg ervoor dat iedere kaart anders is.
- Gooi met de 2 dobbelstenen.
- Maak van de twee getallen die gegooid zijn een keersom. Bijvoorbeeld:
5. Zeg het antwoord niet hardop!
6. Laat iemand de som opschrijven. Als iemand ‘bingo’ zegt, kun je controleren of dit klopt.
7. Staat het antwoord van de keersom op jouw bingokaart? Streep het dan door.
8. Als je 4 antwoorden op een rij hebt doorgestreept, heb je bingo! Wanneer je de bingokaart met 25 vakjes gebruikt, heb je bingo bij 5 antwoorden op een rij.
9. Wie het eerst bingo heeft, heeft gewonnen!Tafelbingo met een bepaalde tafel
Wil je een bepaalde tafel oefenen? Dat kan!
- Als je bijvoorbeeld de tafel van 2 wilt oefenen, vul je de antwoorden van de tafel van 2 in op de lege bingokaarten (er zijn meer vakjes dan antwoorden en daarom vul je een paar antwoorden vaker in). Bijvoorbeeld:
2. Leg nu 1 dobbelsteen met het getal 2 naar boven. Deze laat je zo liggen.
3. Gooi met de andere dobbelsteen.
4. Maak een keersom met de 2 en het getal dat gegooid is. Bijvoorbeeld:5. Zeg het antwoord niet hardop!
6. Laat iemand de som opschrijven. Als iemand ‘bingo’ zegt, kun je controleren of dit klopt.
7. Staat het antwoord van deze keersom op jouw bingokaart? Streep het dan door.
8. Als je 4 antwoorden op een rij hebt doorgestreept, heb je bingo! Als je de bingokaart met 25 vakjes gebruikt, heb je bingo bij 5 antwoorden op een rij.
9. Wie het eerst bingo heeft, heeft gewonnen.Tafelmemory
Download de instructie van tafelmemory
Hoe speel je dit speel?
1. Print de tafelmemory-bladen op een wit of gekleurd A4-papier. Zorg ervoor dat alle kaartjes dezelfde kleur hebben.
2. Knip de kaartjes uit. De keersommen en de antwoorden knip je los van elkaar.
3. Kies welke tafels je wilt gaan oefenen.
4. Pak de kaartjes met de keersommen en de kaartjes met de antwoorden van deze keersommen (je kunt hierbij de tafelkaart gebruiken).
5. Schud de kaartjes en leg ze met de keersommen en antwoorden naar beneden op tafel.
6. Draai om de beurt 2 kaartjes om.
7. Past de keersom bij het antwoord? Dan mag je de kaartjes houden en ben je nog een keer.
8. Past de keersom niet bij het antwoord of heb je 2 keersommen of 2 antwoorden omgedraaid? Dan draai je de kaartjes weer terug en gaat de beurt naar de volgende speler.
9. Wie de meeste kaartjes heeft als alle kaartjes op zijn, heeft gewonnen!Tafelkaartspel
Download de instructie en de tafelkaart
Tafels leren met tafeldomino
Met dit spel kun je de tafels 1 t/m 10 en 11,12,15 en 25 oefenen. Van deze tafels zijn dominokaartjes in het PDF-bestand toegevoegd. Je kunt ook zelf kaartjes maken met het lege blad dat aan het einde van de PDF is opgenomen. Klik op de video voor de uitleg. Onder de video is de link naar de dominokaartjes met de tafels opgenomen.
Je kunt tafeldomino ook kant-en-klaar thuis laten bezorgen. Wel zo makkelijk. Klik hier voor meer informatie over het spel Domino – de tafels van vermenigvuldiging.
Download de dominokaartjes en de instructie
Tafels oefenen met het tafelhappertje
Een leuk idee van Marcel Schmeier, eigenaar van Onderwijsgek.nl en auteur van het boek Effectief rekenonderwijs op de basisschool, is het ’tafelhappertje’. De meeste kinderen vinden het leuk om met het tafelhappertje te werken. Je kunt voor elke tafel een happertje maken en je kunt bijvoorbeeld een happertje maken met de tafelsommen die je kind nog lastig vindt.
OefenbladFlitskaarten Tafels groep 4/5 (Gratis)
Hieronder vind je ook nog een link naar het pakket voor het oefenen van de tafels van het team van Wijzer over de Basisschool. Jullie hebben dus genoeg materialen om samen lekker mee aan de slag te gaan.
Wist je bovendien dat je tafels ook bewegend kunt oefenen? Je leest er meer over in ons artikel bewegend leren rekenen.
Veel succes met oefenen!BundelkortingRekenbox – Tafels van Vermenigvuldiging
Oorspronkelijke prijs was: 72,89.59,00Huidige prijs is: 59,00.
Gerelateerde artikelen
Reacties
34 reacties op “Tafels oefenen: uitleg en de beste oefentips”Geef een reactie






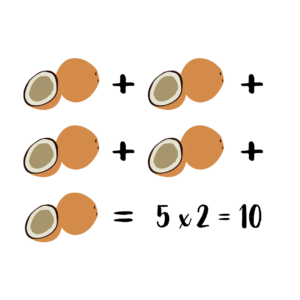




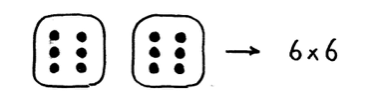
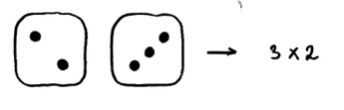











het is leuk
Fijn om te horen Fatoumata!
Graag gedaan.
Succes!
Hartelijke groet,
Carola
Wat is heel leuk om tafels te oefen hartelijk dank voor de praktijk manier ik uitprobeert met mij zoon
Echt super. Me dochter vliegt erdoorheen door de stof. Ze liep een beetje achter maar sinds 2 weken gaat ze met stappen vooruit. Zelfs complimenten gehad van de juf. Top dank je wel Maaike 👍
heel handig