Maten omrekenen: een handig ezelsbruggetje

Door Mirjam Schumacher, BEd Master SEN

Wat is een maateenheid?
Maatbegrip vergroten
Kan het dametje met de centimeter meten
Ezelsbruggetje maten omrekenen: video
Omtrek of oppervlakte?
Spelletjes en lego gebruiken
Wat kun je doen voor echt goed inzicht?
Hoe bereken je de inhoud?
Hoe reken je inhoudsmaten om?
Van dl naar ml
Omrekenen van cm3 naar liters
Gewicht omrekenen
Rekenen meten oefenen? Bekijk de tip:

‘Meten’ en maten omrekenen zijn een belangrijke onderdelen van het rekenen. Eigenlijk zijn kinderen al met meten bezig als ze in groep 2 aan het overgieten zijn bij de watertafel.

In de volgende jaren leren ze steeds meer over meten door uitproberen, vergelijken enzovoorts. Bij het rekenen in groep 5 krijgen ze al te maken met millimeter, decimeter, hectometer en kilometer. Zolang het concreet blijft, hebben de meeste kinderen niet zoveel moeite met dit onderdeel.

De problemen met meten ontstaan meestal pas in groep 7/8. Op dat moment wordt het allemaal namelijk wat abstracter. De formules voor oppervlakte en omtrek worden geïntroduceerd (en vaak door elkaar gehaald) en je kind moet alle maten omrekenen en dan ook nog in de vorm van verhaaltjessommen. Op dat moment zien veel kinderen door de bomen het bos niet meer.

In dit artikel lees je hoe je je kind hiermee kunt helpen. Verderop in dit artikel staat verschillende ‘trucjes’ en hulpmiddelen om maten om te rekenen. Maar je kind zal de ‘trucjes’ en formules pas goed kunnen onthouden en gebruiken als het snapt hoe het zit. Waarom 2 nullen erbij of eraf als het over oppervlakte gaat, en waarom 3 nullen als het over inhoud gaat? Wat is het verschil tussen oppervlakte en omtrek? Wat is het verband tussen meters en liters? Allemaal vragen die in dit artikel beantwoord zullen worden.

Bekijk ook:

Wat is een maateenheid?

Meters, centimeters, liters….het zijn allemaal maateenheden. Maar wat wordt daar nu eigenlijk mee bedoeld?

Je kunt je kind dit laten ervaren door het bijvoorbeeld de lengte van de tafel op te laten meten met zijn handen: hoeveel handen passen er naast elkaar op de tafel. Tegelijkertijd meet jij de lengte met een andere maat, bijvoorbeeld je onderarm. De tafel is dan bijvoorbeeld 15 handen, of 5 onderarmen. Het is dus maar net waarmee je meet. In dit geval is de maateenheid van je kind dus ‘hand’ en die van jou ‘onderarm’.

Vroeger werden deze maateenheden echt gebruikt: palm, duim, voet, el: allemaal maten die met alleen met onderdelen van het lichaam gemeten konden worden. Maar het is ook duidelijk dat op die manier natuurlijk niet heel precies gemeten kon worden.

Per land verschilden de maateenheden dan ook nog. Om die reden is in het begin van de 19 de eeuw het tientallig meetstelsel ingevoerd. Wat nog wel vrij lang in gebruik bleef, waren maten zoals 1 ons (100 gram), een pond (500 gram), een dozijn (12) en een gros (144). De eerste 2 mogen officieel niet meer gebruikt worden in winkels en advertenties.

Maatbegrip vergroten

Als je kind bij de diverse maten een concreet beeld heeft, zal het makkelijker met maten kunnen rekenen. Daarom is het goed om nog even terug te stappen in de 18 de eeuw: laat je kind aan het eigen lichaam ontdekken wat een centimeter, decimeter enz. is. Hier zijn wat voorbeelden, maar je kind ontdekt misschien wel andere maateenheden.

1 mm is de dikte van je nagel
1 cm is de breedte van een nagel
1 dm is de lengte van het puntje van je duim tot het begin van je pols.
1 m is een hele grote stap.

Tot zover de maten die concreet met behulp van het lichaam gemeten kunnen worden. Laat je kind verschillende voorwerpen opmeten met deze hulpmiddelen. Ook leuk: laat je kind zijn armen opzij strekken en meet de afstand tussen de middelvingertoppen. Meet daarna de lengte van je kind. Je zult zien dat die maten hetzelfde zijn. Voor de grotere maten kun je denken aan:

1 decameter (10 meter, dus 10 grote stappen) is bij een rijtjeswoning vaak de afstand van voordeur tot achterdeur.
1 hectometer (100 meter): misschien de afstand van jullie huis naar het huis van een vriendje verderop in de straat. Probeer iets te vinden dat makkelijk te onthouden is, en probeer deze afstand in 100 hele grote stappen af te leggen.
1 kilometer: ga hiervoor naar Maps en probeer een punt te vinden dat ongeveer 1 km is vanaf jullie huis: de school, de supermarkt enz. Mooi moment om ook even in te gaan op de schaal van de kaart. Helemaal rechts onderin het scherm staat de schaal vermeld. 1 km is ook de afstand die je ongeveer kunt lopen in 12 minuten.

Laat je kind met de lichaamsmaten ervaren dat iedere maat 10 keer in de volgende maat past. Dus laat het met vingers naast elkaar de lengte van jouw hand (dm) meten en concluderen dat dat (ongeveer) 10 vingers zijn, en laat het een hele grote stap zetten en dit weer nameten met de dm aan zijn eigen hand (10) maar ook met de vingers.

Laat dit allemaal tenslotte ook zien op een meetlint of rolmaat: 10 kleine streepjes (mm) in een cm, 10 cm in een dm, dus 10×10 mm in een dm. Maar ook andersom: in een meter zitten 10 decimeters, in een decimeter 10 cm en 100 mm.

Oefenbladen Rekenen Groep 6 (Gratis)

Oefenbladen Rekenen Groep 7 (Gratis)

Oefenbladen Rekenen Groep 8 (Gratis)

Kan het dametje met de centimeter meten

Je kind is nu klaar voor onderstaand ‘trucje’, wat overigens nu dus niet meer als trucje ervaren wordt, maar als een handig schema. Om de namen van de opeenvolgende maten te onthouden, is een ezelsbruggetje altijd handig. Een ezelsbruggetje kan heel goed helpen om de feiten die je kind heeft geleerd (en heeft begrepen) te onthouden.

Uit onderzoek blijkt dat het aanleren van geheugenstrategieën zoals ezelsbruggetjes een zeer effectieve leerstrategie is (Bron: Wat écht werkt, 27 evidence based strategieën voor het onderwijs, David Mitchell, 2015). Het ezelsbruggetje om de volgorde van de maten te onthouden is: Kan het dametje met de centimeter meten.

Kan (=km) het (=hm) dametje (=dam) met (=m) de (=dm) centimeter (=cm) meten (=mm)

Kinderen onthouden dit zinnetje beter als je het in kleur opschrijft, voor iedere woord een andere kleur, en deze een poosje naast hun bed, op het toilet of op de koelkastdeur plakt. En door er een tekening of toneelstukje bij te maken. Als je kind dit zinnetje uit het hoofd leert, kan het altijd makkelijk het volgende rijtje opschrijven.

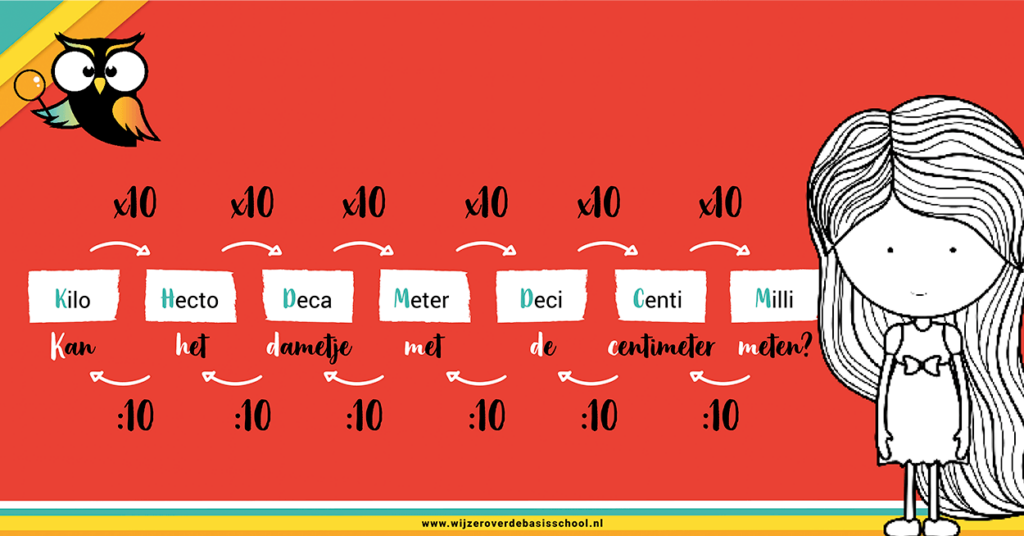
Elke stap naar rechts is vermenigvuldigen met 10 en elke stap naar links is delen door 10. Ezelsbruggetje: naar rechts is keer, naar links is delen.

Bekijk de video over het ezelsbruggetje en het schema en ga aan de slag met oefenen.

Ezelsbruggetje maten omrekenen: video

Sommige kinderen haken af omdat het schema er ingewikkeld uitziet, of omdat ze richting van de pijlen niet kunnen onthouden. Veel kinderen hebben dan baat bij het leren van de volgende regels:

Als ik om moet rekenen naar een kleinere maat, wordt het getal groter. Ik moet dus vermenigvuldigen (keer). De komma gaat naar rechts en/of er komen nullen bij.
Als ik moet omrekenen naar een grotere maat, wordt het getal kleiner. Ik moet dus delen. Er gaan nullen af en/of de komma verschuift naar links.

Voorbeeld:

Hoeveel dam is 4000 cm? Ik reken om naar een grotere maat, dus het getal wordt kleiner, dus delen. Vanaf dam is het 3 stappen naar links. Je gaat dus delen door 1000. 4 dam = 4000 cm.

5,3 km is hoeveel meter? Ik reken om naar een kleinere maat, dus ik moet vermenigvuldigen. Het zijn 3 stapjes dus ik vermenigvuldig met 1000 (de komma verschuift naar rechts en dan komen er nog 2 nullen bij).

Omtrek of oppervlakte?

Lengtematen worden ook gebruikt om de omtrek aan te geven. Veel kinderen halen oppervlakte en omtrek door elkaar. Ze kennen de formules vaak wel, maar weten niet welke formule bij wat hoort.

Het helpt als je er een spelletje van maakt: Laat je kind terwijl jij niet kijkt, verschillende voorwerpen omtrekken: een vaas, een boek, maar ook onregelmatigere vormen. Vervolgens moet jij gaan raden welke voorwerpen het omgetrokken heeft. Gebruik hierbij vaak het woord omtrek.

Na dit spelletje een paar keer gespeeld te hebben (herhaling doet wonderen!) blijft het begrip omtrek hopelijk beter hangen. Je kunt nu met een meetlint verschillende omtrekken gaan meten. Kleine omtrekken: een bord, schoteltje, maar bijvoorbeeld ook de tafel. Bedenkt je kind zelf dat het bij de tafel voldoende is om alleen de lengte en de breedte op te meten en die dan keer 2 te doen? Dan heeft het zelf de formule voor omtrek ontdekt! Ontdekt je kind het zelf niet? Laat het rustig de hele omtrek meten, en ‘bewijs’ dan zelf dat de formule werkt.

Laat je kind vervolgens verschillende figuren tekenen. De omtrek van de onregelmatige figuren rekent het dan uit door met het potlood de omtrek te volgen en de lengten van de lijnstukjes op te tellen. Die van de regelmatige figuren (rechthoeken) door de formule te gebruiken.

Spelletjes en lego gebruiken

Als je kind eenmaal goed begrijpt wat omtrek is, zal het de formules niet zo snel meer door elkaar halen. Maar toch is het belangrijk dat het goed begrijpt wat oppervlakte dan is, en waarom de oppervlaktematen op een andere manier omrekent dan de lengtematen.

Gebruik vierkante legoblokjes of iets dergelijks. Leg een bord of dienblad vol met de blokjes (naast elkaar) en tel hoeveel erop passen. Zeg dan: er passen 35 legoblokjes op. De oppervlakte van dit bord is 35 legoblokjes.

Om het begrip oppervlakte nog beter in te slijpen, kun je er weer een spelletje van maken: laat je kind zelf, zonder dat jij het ziet, de oppervlakte van verschillende kleine voorwerpen bepalen. Jij moet vervolgens raden welke voorwerpen het heeft gemeten. Gebruik hierbij vaak de woorden ‘erop passen’ en ‘oppervlakte’. De link tussen deze twee begrippen moet stevig verankerd worden.

Net als bij de lengtematen zal je kind nu ook snappen dat het niet handig is om de oppervlakte in legoblokjes aan te geven. We gebruiken daar natuurlijk ook standaard maateenheden voor.

Wat kun je doen voor echt goed inzicht?

Teken een vierkant van 10 bij 10 op een blad met hokjes van 1 cm2 (of, nog beter, van 1 mm2) en schrijf daarin ‘1 dm2’. Laat je kind tellen hoeveel hokjes van 1 cm2 er zijn. Bedenkt het zelf al dat je dan het aantal rijen moet vermenigvuldigen met de lengte van deze rijen? Dan heeft het zelf de formule voor oppervlakte (oppervlakte = lengte x breedte) ontdekt. 1 dm2 is dus 100 cm2. Heb je millimeterpapier dan kun je je kind ook nog laten bedenken hoeveel mm2 er in de cm2 passen (ook weer 100) en hoeveel er dan in de decimeter passen (100 keer 100 dus 10.000).

Je kind snapt nu dat bij de oppervlaktematen bij de oppervlaktematen iedere maat 100 keer in de volgende maat past. Dus ieder stapje in het schema betekent bij de oppervlaktematen: delen of vermenigvuldigen met 100! Achter de maat komt dan een 2’tje te staan om aan te geven dat er twee grootheden vermenigvuldigd zijn, namelijk lengte keer breedte. Wel makkelijk, dat 2’tje, want zo kun je ook onthouden dat er per keer 2 nullen af gaan of bijkomen. De rest van het schema blijft hetzelfde, alleen de keer 10 en gedeeld door 10 wordt dus keer 100 en gedeeld door 100.

Hier volgen weer een aantal voorbeelden om de oppervlaktematen zodat je kind zich er weer een beeld van kan maken.

1 mm2 is een stipje
1 cm2 is ongeveer de oppervlakte van je nagel
1 dm2 is ongeveer de oppervlakte van je hand.

Laat je kind zijn hand omtrekken op papier met ruitjes van 1 cm2 en de hele en halve ruitjes optellen. (Ook leuk: kijk hoeveel smarties er op zijn hand passen. Leuke herinneringen worden beter onthouden).

1 m2: hiervoor kun je zelf het beste op zoek gaan naar iets in je huis. De afmeting van jullie (rechthoekige) salontafel. Of de afmeting van de douchebak.
1 dam2: bij een rijtjeshuis ongeveer 2 achtertuinen. Of misschien is er wel een speeltuintje in jullie buurt wat ongeveer zo groot is.
1 hm2: ongeveer zo groot als 1,5 voetbalveld.
1 km2: kijk ook hier weer voor op Google maps. Misschien de oppervlakte van het stadscentrum of een recreatieplas/bos in de buurt.

Hoe bereken je de inhoud?

Voor een uitgebreide uitleg met voorbeelden en video klik hier: inhoud berekenen uitleg.

Laat je kind eerst zelf weer de formule (inhoud = lengte x breedte x hoogte) ontdekken. Gebruik een leeg doosje en iets stapelbaars om het mee te vullen, bijvoorbeeld snoepjes of legoblokjes. Laat je kind eerst de oppervlakte van de bodem vol leggen.

Hoeveel rijen van hoe lang?
Wat is dus de oppervlakte?
Vervolgens vraag je: hoeveel van deze lagen passen er in het doosje.

Misschien gaat je kind het doosje helemaal vullen, of misschien bedenkt het dat het dan maar één torentje hoeft te maken.

Als het aantal lagen bepaald is, vraag je hoeveel blokjes/snoepjes er dan in het doosje passen.

Dat is dus de eerste laag keer (lengte keer breedte) keer de hoogte. Leg de verbinding met de standaardmaten door te vragen hoeveel blokjes van 1 cm3 er in het doosje passen. Je kind kan het doosje dan opmeten en de inhoud uitrekenen in cm3. Laat het daarna van nog een aantal doosjes de inhoud uitrekenen.

Hoe reken je inhoudsmaten om?

Gebruik legoblokjes of iets anders rechthoekigs. Vraag je kind om de vorm van dat blokje 10 keer zo groot te maken. Laat het zelf ontdekken dat je dan zowel de lengte als de breedte als de hoogte 10 keer zo groot moet maken (anders is de vorm niet hetzelfde). Met andere woorden, je hebt er 1000 blokjes voor nodig! Je kind kan nu snappen dat voor iedere stap verder bij de inhoudsmaten betekent: vermenigvuldigen met 1000!

Hieronder staan weer wat inhoudsmaten zodat je kind zich er weer een voorstelling van kan maken:

1 mm3 is zo groot als een korreltje suiker
1 cm3: de houten blokjes waarmee ze op school leren rekenen, of een minisuikerklontje (waarin dan dus 1000 korreltjes zitten)
1dm3: is hetzelfde als een liter. Dus bijvoorbeeld een pak vla.
1 m3: zoek op Google maps een afbeelding van een kuub zand. Je kind heeft zo’n grote zak vast weleens zien staan in een nieuwbouwwijk.
1 dam3: ongeveer de inhoud van de eerste 4 verdiepingen van een woontoren.
1 hm3: ongeveer de inhoud van zo’n enorm cruiseschip (Google afbeeldingen)
1 km3: 1000 van de cruiseschepen.

Van dl naar ml

Hierboven ging het over de inhoud in cm3. Maar als het over vloeistof gaat, maar ook bij bijvoorbeeld potaarde en deodorant, wordt de inhoud vaak in liters of centiliters aangegeven. Bekijk met je kind eens allerlei verpakkingen waarop inhoud aangegeven staat. De ene keer wordt het aantal liters vermeld, bijvoorbeeld op melkpakken, maar op veel andere verpakkingen worden milliliters of centiliters gebruikt. Voor het omrekenen van de maten van de liters kan hetzelfde schema worden gebruikt als dat voor de lengtematen. Het ezelsbruggetje klopt bijna, maar kan aangepast worden: in plaats van meter komt dan de liter.

Daarmee wordt ook gelijk de hele samenhang duidelijk tussen meters, liters en ook grammen. Overigens worden de begrippen kiloliter, hectoliter en decaliter zelden gebruikt en ook op school wordt daar zelden mee gerekend.

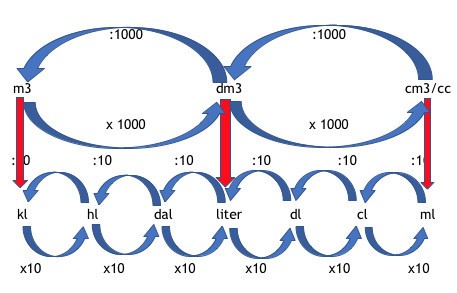
Omrekenen van cm3 naar liters

Soms is het handig dat je cm3 om kunt rekenen naar liters. Als je bijvoorbeeld wilt weten hoeveel water er in je aquarium of zwembad zit, of wat de inhoud van je huiskamer is. Hoe reken je dit om?

Wil je je kind dit weer zelf laten ontdekken? Neem dan een leeg pak melk, en giet daar een liter water in. Laat je kind nu de inhoud uitrekenen in cm: de maten van de bodem (lxb) keer de hoogte van het water. Als het goed is komt het dan uit op zo’n 1000 cm3. Met de omrekentabel kun je concluderen dat 1000 cm3 hetzelfde is als 1 dm3. Een liter is dus hetzelfde als 1 dm3!

Zoals je weet gaan er 1000 cm3 in een dm3, maar bij de liters zijn er dus extra tussenstapjes gemaakt. Er gaan net zoals bij de meters 1000 ml in een liter, maar daartussen zitten nog (ook net als bij de lengtematen) nog de centiliter en deciliter. Je kunt dat je kind uitleggen door het korreltje suiker en de kubieke meter zand te laten zien. Dan wordt het logisch dat er behoefte was aan de tussenmaten, omdat je anders wel met heel veel nullen moet rekenen. Ook nog handig om te weten: 1 liter vloeistof weegt ongeveer 1 kilogram. Het zo zijn we aangekomen bij het onderwerp gewicht.

Gewicht omrekenen

Laat je kind eerst weer een gevoel krijgen bij wat ongeveer een gram, ons of kilo weegt. Als je een brievenweegschaal hebt, kun je voorwerpen opzoeken die 1 gram wegen. Alles wat daaronder zit (decigram, centigram en milligram) is lastig om thuis te wegen, net zoals een ton.

Hiermee krijgt je kind een idee:

Een snufje zout weegt 1 mg
Een veertje weegt 1 cg (10 mg)
Een paperclip weegt 1 dg (meestal aangeduid als 0,1 gr)
Een cashewnootje weegt 1 gr
Een muntstuk van 2 euro weegt 1 decagram (10 gram)
Een pakje broodbeleg weegt 1 hectogram (100 gram, 1 ons)
Een pak suiker weegt 1 kg
Een paard (of een gewone auto) weegt 1 ton (1000 kg).

In de praktijk worden alleen de mg, gram en kg gebruikt, maar voor het omrekenen is handig om de tussenmaten ook te herkennen. Dan kan ook weer hetzelfde omrekenschema gebruikt worden als voor de lengtematen en de liters. De ons en het pond mogen officieel niet meer worden gebruikt, maar je kind moet nog wel weten hoeveel het is. Een ons is 100 gram en een pond is 500 gram oftewel 0,5 kg.

In dit liedje wordt uitgelegd wat de woorden ‘ons’ en ‘pond’ betekenen:

Veel plezier met spelen en oefenen!

Rekenen meten oefenen? Bekijk de tip:

Bestel de oefenboeken rekenen van Aandacht voor Rekenen om meten, gewichten en inhoud en vele andere onderdelen in te oefenen. Naast kale sommen zijn er ook veel redactiesommen over meten, gewichten en inhoud opgenomen in de oefenboeken. Deze redactiesommen komen ook veel voor in de cito toetsen rekenen.

Klik hier om de oefenboeken te bekijken: Oefenboeken rekenen groep 3 t/m 8