Dit artikel vertelt je alles wat je moet weten over inhoud, inhoud berekenen en de verschillende maateenheden die je voor de inhoud kan gebruiken.
Ook leer je hoe je inhoudsmaten kunt omrekenen naar andere maten. Zo weet je straks bijvoorbeeld hoeveel kubieke decimeter 1 liter is! Dit artikel is een vervolg op de uitleg over het metriek stelsel. Bekijk ook onderstaande video’s over het metriek stelsel en hoe je inhoud berekent.
Hoe kun je de inhoud van iets berekenen?
Hoeveel liter water er in een rechthoekige emmer zit, kun je natuurlijk schatten. Maar dat is nog niet zo makkelijk. Daarom is het handig als je de inhoud ervan kunt berekenen.
Waar dat goed voor is?
Als je weet hoeveel liter water er in de emmer zit, weet je ook hoeveel keer je heen en weer moet lopen om jullie nieuwe, opblaasbare zwembad te vullen. En of je dat alleen aankan, of dat je beter iemand kunt uitnodigen om je te helpen!
De berekening die je moet maken om de inhoud van een kubus of een balk te berekenen, is als volgt:
lengte x breedte x hoogte
We leggen je zo precies uit hoe dat dan werkt met die berekening.
Voordat we dat doen, vertellen we je wat meer over het metriek stelsel dat je gebruikt voor berekeningen van de inhoud.
Bekijk ook:
- Metriek stelsel oefenen en uitleg
- Maten omrekenen: een handig ezelsbruggetje
- Meten en meetkunde: 5 handige weetjes
- Oppervlakte berekenen
- Schaal berekenen
- Omtrek berekenen
- Km naar m omrekenen
- Rekenen oefenen met de beste handleiding voor ouders
Hoe je met het metriek stelsel inhoud berekent
Je weet vast al wat het metriek stelsel is. Je gebruikt het om aan te geven hoe groot (meter) of zwaar (gram) iets is. Je kunt het metriek stelsel ook gebruiken om aan te geven welke hoeveelheid ergens in past. Dan spreek je over de inhoud.
Denk maar aan een pak melk. Als je het over inhoud hebt, gebruiken we in het metriek stelsel meestal liter als eenheid. Daarnaast kun je kubieke meter (m³) gebruiken. Hoe het zit met dat drietje boven die ‘m’ van meter, leggen we je later uit. Hieronder leer je eerst hoe het metriek stelsel voor liters en kubieke meters werkt.

Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 7 (Gratis)
Metriek stelsel liter

Stel, je krijgt de volgende opgave: In een emmer zit 10 liter water. Hoeveel deciliter zit er in de emmer?
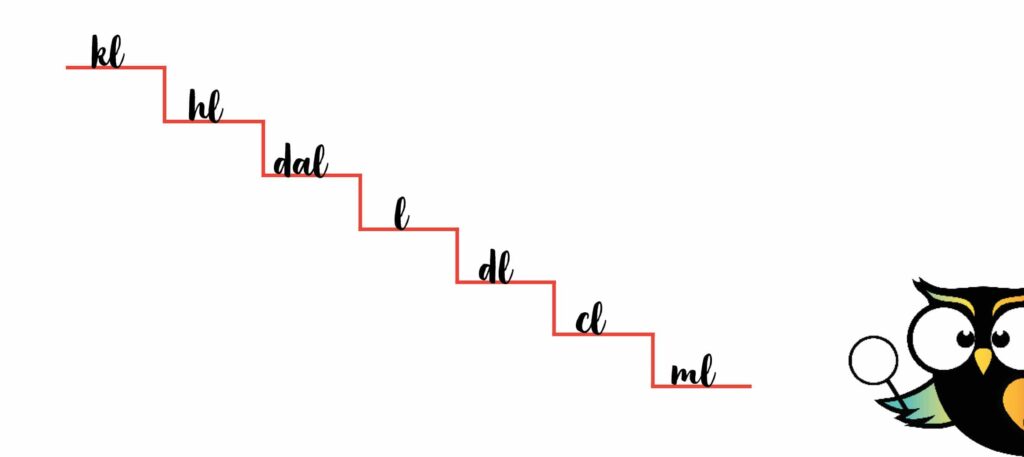
Als je deze som goed wilt uitrekenen, moet je de trap van het metriek stelsel van liters gebruiken. Eerst teken je daarvoor een trap:
Zoals je misschien nog wel weet van de trap van meters, kun je een ezelsbruggetje gebruiken om te onthouden wat de volgorde van de maateenheden is. Het zinnetje dat je daarvoor gebruikt is:
Alle eerste letters van de woorden helpen je de trap te vullen. Kijk maar mee:
- Kan = kiloliter (kl)
- Het = hectoliter (hl)
- Dametje = decaliter (dal)
- Met = eigenlijk ‘meter’, maar hier maken we er ‘liter’ van, omdat dit de trap van de liters is. (l)
- De = deciliter (dl)
- Centimeter = centiliter (cl)
- Meten = milliliter (ml)
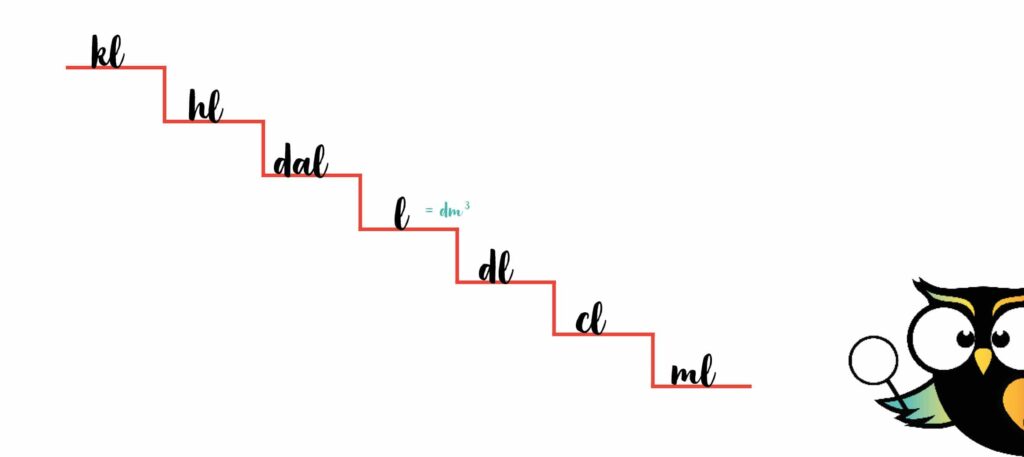
Dat betekent dat de volledige trap voor liters er zo uitziet:
Je weet vast nog wel dat je bij 1 stap naar rechts het aantal keer 10 moet doen. Als je bijvoorbeeld 100 liter hebt, betekent dat 100 x10 = 1000 deciliter.
100 liter is ook:
– 10.000 centiliter
– 100.000 milliliter
Als je een stap naar links zet, dan deel je door 10. Dat betekent dat 100 liter hetzelfde is als:
– 10 decaliter
– 1 hectoliter
– 0,1 kiloliter
Als je dit weet, kun je alle sommen maken die jou iets vragen over de inhoud in liters.
Laten we eens een voorbeeldsom bekijken:
Moeder heeft 1 liter ranja in een kan. Ze wil voor de kinderen glazen vullen. In een glas past 200ml ranja. Hoeveel glazen kan moeder dan vullen?
Als je hier een antwoord op wilt, moet je de liter ranja eerst omrekenen naar milliliters. Want als je weet hoeveel milliliter ranja moeder heeft, weet je ook hoeveel glazen ze kan vullen. Pak daarom de trap erbij.

Je moet van een liter naar milliliter, dus je moet naar rechts. Als je naar rechts gaat, doe je per stap x10.
Eerst ga je van liters naar deciliters:
1 liter = 1 x 10 = 10 deciliter
Dan ga je naar centiliters.
10 deciliter = 10 x 10 = 100 centiliter
En als laatste ga je naar milliliters.
100 centiliter = 100 x 10 = 1000 milliliter
Nu weet je dus dat moeder 1000 ml ranja heeft.
Je kunt nu de som uitrekenen.
Je weet dat in 1 glas 200ml ranja past. Hoe vaak kan moeder schenken? Met andere woorden: hoe vaak past 200ml in de kan met ranja? Om dat te weten, deel je 1000 door 200. Het antwoord van 1000 / 200 = 5. Moeder kan dus 5 glazen ranja vullen.
Inhoud berekenen in m³
In Nederland werken we meestal met de maateenheid liters om aan te geven hoeveel inhoud iets heeft. Bijvoorbeeld hoeveel melk er in een pak zit, hoeveel water in een zwembad past of hoeveel zand in een zandbak.
Maar… we werken in Nederland met nóg een maateenheid als we het over inhoud hebben. Dat zijn namelijk de kubieke meters, kubieke centimeters of kubieke decimeters. Want weet je nog hoe je de inhoud moet berekenen? We doen dan altijd lengte x breedte x hoogte.
Het antwoord dat je krijgt is altijd in ‘kubieke’. Met dat kleine drietje boven de maat, bijvoorbeeld m³, cm³ of dm³. Dat drietje staat er omdat je 3 afmetingen combineert met elkaar: lengte, breedte en hoogte.
- Alleen de lengte (1 afmeting) geeft bijvoorbeeld een afstand in meters (m).
- Als je lengte x breedte doet (2 afmetingen), krijg je de oppervlakte in vierkante meters (m²).
- Doe je lengte x breedte x hoogte (3 afmetingen), dan krijg je de inhoud in kubieke meters (m³).
Laten we eens kijken naar een voorbeeld.
Een zwembad heeft een lengte van 6 meter, een breedte van 4 meter en een diepte van 2 meter. Als je de inhoud van dit zwembad wilt uitrekenen, doe je lengte x breedte x hoogte. Je krijgt dan 6 x 4 x 2 = 48
Omdat alle drie de afmetingen een ‘m’ achter zich hebben staan, krijg je nu m³. De inhoud van dit zwembad is dus 48 m³.
Inhoud omrekenen van liter naar m³ of andersom
We weten nu dat je de inhoud van een zwembad in liters kunt berekenen, maar ook in kubieke meters. En weet je wat leuk is? Je kunt de maateenheid van liters ook omrekenen naar kubieke meters en andersom! Ingewikkeld? Dat valt gelukkig mee.
Je kent de trap of lijn van de liters al. Om je geheugen op te frissen, vind je hem hieronder nog een keer.

Je kent ook de trap of lijn van de kubieke meters al. Die ziet er zo uit.
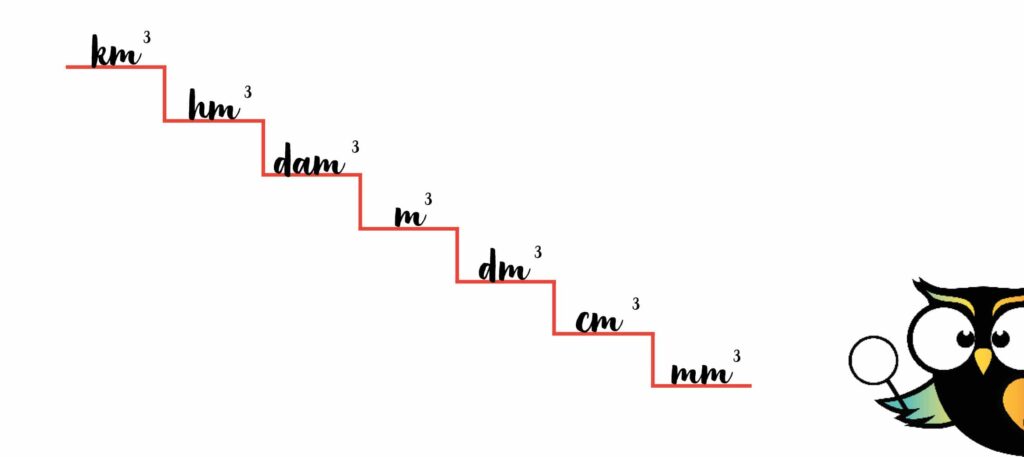
Je ziet dat de lijnen heel erg op elkaar lijken, maar er is wel 1 groot verschil! Als je op de lijn van de liter een stap naar links gaat, deel je door 10.
Bij de kubieke meters deel je niet door 10, maar door 1000. Dat komt door dat kleine 3’tje boven de ‘m’. Door dat 3’tje weet je dat je steeds met stappen van 1000 moet rekenen.
Deze twee maten, of deze twee trappen, hebben alles met elkaar te maken.
Hoe dat komt, laten we je zien met een fles water van precies 1 liter en met een kubus. De kubus is 1 dm lang, 1 dm breed en 1 dm hoog. De inhoud van de kubus is dus 1 x 1 x 1 = 1dm³.
We gieten nu de fles van 1 liter in de kubus. Als we dat doen, zien we dat 1 liter precies in 1 kubieke decimeter (dm³) past!
1 liter is dus precies hetzelfde als 1 dm³.
Of:
1 l = 1 dm³
Dat betekent dat je op de trap bij liters ook kubieke decimeters kunt schrijven, omdat dit precies hetzelfde is.
Hetzelfde trucje kunnen we doen met 1 milliliter (ml) water en een kubus van 1 kubieke centimeter (cm³).
Ook hier geldt: 1 ml water past precies in de kubus van 1 cm³!
1 ml = 1 cm³
En hetzelfde geldt voor 1 kiloliter (kl) en 1 kubieke meter (m³).
1 kl = 1 m³
Nu kun je dus de trap van het metriek stelsel van liters aanvullen met deze informatie.
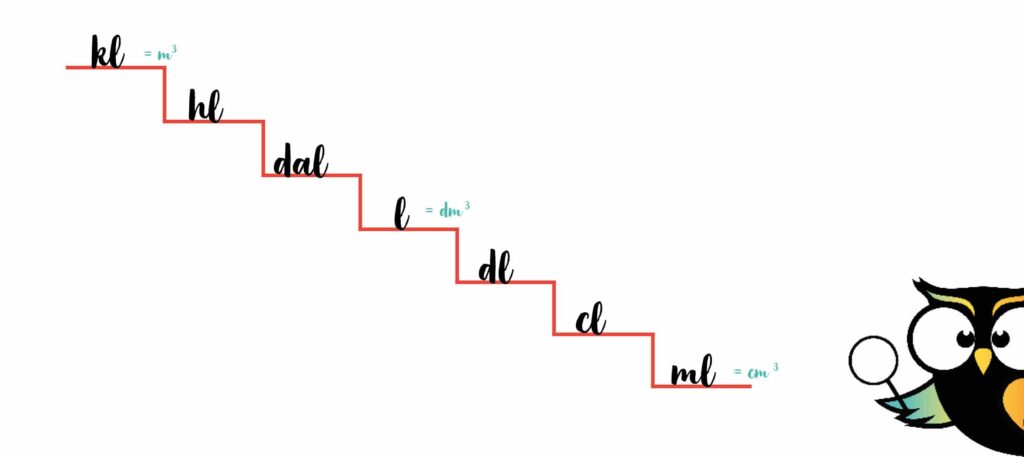
Handig, die trap! Daarmee kun je zonder problemen alle inhoudsmaten omrekenen. Van liters naar kubieke meters en andersom. We zeiden toch dat het niet moeilijk was?
-
Rekenpakket Groep 7 – 2e helft schooljaar (Cito-IEP)
Oorspronkelijke prijs was: 59,90.54,00Huidige prijs is: 54,00. BundelkortingIn mijn winkelwagen Bekijk detailsVideobijles Rekenen Groep 7
Oorspronkelijke prijs was: 79,00.49,95Huidige prijs is: 49,95. Aanbieding!In mijn winkelwagen Bekijk detailsBreuken en Procenten oefenpakket + videobijles (Cito – IEP)
Oorspronkelijke prijs was: 119,75.87,00Huidige prijs is: 87,00. BundelkortingIn mijn winkelwagen Bekijk detailsJaarpakket Groep 7
Oorspronkelijke prijs was: 575,05.490,00Huidige prijs is: 490,00. Speciaal JaarpakketIn mijn winkelwagen Bekijk detailsInhoudsmaten omrekenen
We geven je nu wat voorbeelden. Gebruik de informatie die hierboven staat om met ons mee te rekenen.
Stel je voor:
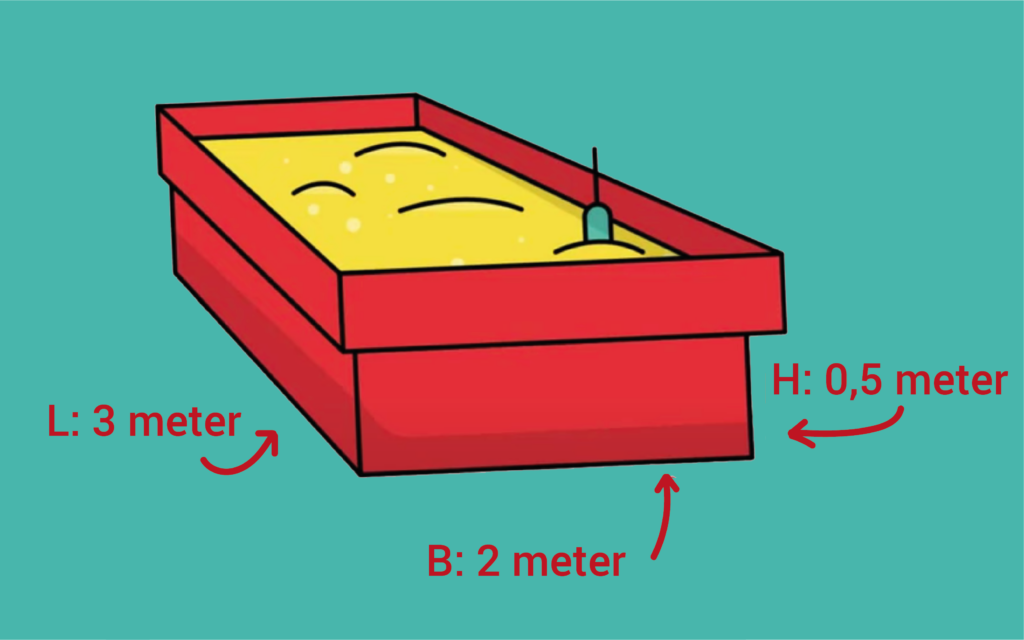
Je wilt de zandbak op het schoolplein vullen met zand. De zandbak is 3 x 2 x 0,5 m. Op de tekening van de zandbak staan netjes de afmetingen in meters.Met deze afmetingen kun je de inhoud van de zandbak in kubieke meters uitrekenen. Dat doen we eerst. Je weet al: inhoud = lengte x breedte x hoogte. Voor deze zandbak geldt: inhoud = 3 x 2 x 0,5 = 3 kubieke meter. De inhoud van de zandbak is dus 3 m³.
Vervolgens ga je naar de winkel waar ze de zakken zand verkopen. Ai, daar loop je tegen een lastigheid aan: op de zakken zand staat vermeld hoeveel liter zand er in een zak zit. Er staat niets op over m³… Hoe weet je nou hoeveel liter je nodig hebt?
Om daar achter te komen, reken je kubieke meters om naar liters. Daarvoor gebruik je de trap.
Op de trap zie je dat helemaal bovenaan de kubieke meters staan, bij de kiloliters. Want weet je nog? 1 kiloliter = 1 m³.
Van de zandbak weet ik dat er 3 m³ in past. Dat is dus ook 3 kiloliter. Nu wil ik weten hoeveel liters er in een kiloliter passen. Daarvoor moet ik een paar stapjes naar rechts.
1 stap naar rechts betekent x 10. Dus 3 kiloliter = 3 x 10 = 30 hectoliter.
30 hectoliter = 30 x 10 = 300 decaliter.
300 decaliter = 300 x 10 = 3000 liter.
Nu weet je dus dat je voor deze grote zandbak op het schoolplein 3000 liter zand nodig hebt!
Nog een andere voorbeeldsom:
2000ml = … dm3
Ook nu neem je de trap erbij.
Je begint bij de milliliters en je zet daar de 2000 neer. Je ziet dat milliliter hetzelfde is als kubieke centimeter. Maar we moeten weten hoeveel kubieke decimeter 2000 milliliter is. Kubieke decimeters is hetzelfde als liters. Dat zijn dus 3 sprongen naar links. 1 sprong naar links betekent delen door 10. Je deelt 2000 dus door 10, nog eens door 10 en dan nog eens door 10. Je ziet nu dat 2000 milliliter hetzelfde is als 2 liter en dus ook als 2 dm³!Inhoud berekenen in groep 7
Als je bezig bent met rekenen in groep 7 zit, leer je allerlei dingen over het berekenen van de inhoud. We zetten hier alle dingen op een rij.
- Je kent de kubieke inhoudsmaten cm³, dm³ en m³
- Je weet dat 1 m³ hetzelfde is als 1000 dm³
- Je weet dat 1 dm³ hetzelfde is als 1000 cm³
- Je kunt inhoudsmaten met elkaar vergelijken. Zo weet je dat in een bak met een inhoud van 1 dm³ 1000 blokjes van 1 cm³ passen, maar ook 1 liter melk.
- Je kunt uitleggen wat het woord ‘kubieke’ betekent.
- Je kent het woord ‘kuub’.
- Het lukt je om litermaten om te rekenen naar kubieke maten en andersom.
- Je kunt de inhoud van een kubus en een balk uitrekenen door lengte x breedte x hoogte te gebruiken.
- Je hebt geleerd hoe je sommen als deze kunt uitrekenen: Een rechthoekige vogelkooi heeft een inhoud van 3 m³. Wat kunnen de afmetingen van deze kooi zijn?
Het kan natuurlijk zijn dat jij net wat meer of minder leert in groep 7. Dat is helemaal niet erg. Iedere school werkt op zijn eigen tempo.
Inhoud berekenen in groep 8
Bij rekenen groep 8 ga je verder waar je aan het eind van groep 7 gebleven bent. Je herhaalt veel over inhoudsmaten en berekeningen. Ook komen er nog wat nieuwe dingen bij.
- Je kent de trappen van inhoudsmaten in liters en m³. Je kunt ze uitleggen en gebruiken bij berekeningen.
- Je leert wat er gebeurt met de inhoud van een figuur als je 1 van de afmetingen (lengte, breedte of hoogte) verdubbelt. Als je bijvoorbeeld een balkvormige pak koekjes 2 x zo hoog maakt, hoeveel keer zo groot wordt de inhoud dan?
- Je leert hoe je om moet gaan met sommen als deze: Als je de lengte van 1 zijde van een kubus weet, hoe kun je dan de inhoud weten?
Inhoud berekenen: het lijkt moeilijk, maar het valt mee!
De inhoud van iets berekenen lijkt misschien moeilijk, maar dat is het eigenlijk niet. Zolang je maar gebruik maakt van de trappen die we je hierboven hebben uitgelegd. Heb jij nog goede tips over het berekenen van de inhoud? Of heb je nog een vraag? Laat het ons weten in een reactie hieronder!
We vinden het leuk om wat van je te horen. Zo maken we samen van inhoud berekenen een onderwerp dat iedereen begrijpt!
OefenbladOefenbladen Doorstroomtoets Groep 8 (Gratis)
OefenbladOefenbladen Begrijpend lezen Groep 8 (Gratis)
OefenbladWerkbladen Spelling Groep 8 (Gratis)
OefenbladOefenbladen Rekenen Groep 8 (Gratis)
OefenbladOefenbladen Cito/IEP-toets Groep 7 (Gratis)
OefenbladOefenbladen Rekenen Groep 7 (Gratis)
Gerelateerde artikelen