Meten en meetkunde: 5 handige weetjes

In het dagelijks leven meet je regelmatig dingen op. Maar wist je dat je kind ook op de basisschool tijdens het rekenen al regelmatig te maken krijgt met meten en meetkunde?

In dit artikel vertellen we je wat meetkunde is. Bovendien geven we je 5 handige weetjes die jou en je kind helpen de wereld van meten en meetkunde beter te begrijpen.

Wat is meten en meetkunde?

Als je in het woordenboek de definitie van meten zoekt, vind je dit:

Meten: de lengte, de oppervlakte of de inhoud van iets bepalen

Ook gewicht, tijd en temperatuur zijn meetbaar. Op de basisschool wordt aan al deze dingen aandacht besteed. In dit artikel gaan we vooral in op lengte, gewicht en inhoud.

In het dagelijks leven meet je heel wat dingen:

• hoeveel je kind gegroeid is;
• hoe groot je tuin is;
• hoeveel boter er in het cakebeslag moet;
• hoelang je kind erover doet om 100 meter te sprinten.

En dit zijn nog maar enkele voorbeelden.

Je kind leert op de basisschool hoe het bepaalde dingen moet meten met meetinstrumenten. Bijvoorbeeld met een liniaal of een maatbeker. Die praktische benadering maakt dat je kind ook later in zijn leven makkelijk met dit soort metingen om kan gaan.

Meetkunde

Op de basisschool wordt ook een begin gemaakt met eenvoudige vormen van meetkunde.

Bij meetkunde gaat het niet zozeer om het op- of afmeten van dingen, maar om (ruimtelijk) inzicht. Je kind krijgt bijvoorbeeld meer inzicht in:

• plattegronden
• 2- en 3-dimensionale vormen
• symmetrie
• patronen

Zo maakt je kind bijvoorbeeld kennis met kubussen, cilinders en kegels. Ook leert het hoe het een plattegrond moet aflezen en hoe verhoudingen werken.

Meten en meetkunde: 5 handige weetjes

Wanneer je je kind moeite heeft met meten en meetkunde, is het natuurlijk handig als je hem thuis met dit onderdeel kunt helpen. Hieronder staan 5 belangrijke weetjes over meten en meetkunde, waar je thuis je voordeel mee kunt doen.

Lees de weetjes samen met je kind door en bespreek ze uitgebreid. Zoek naar voorbeelden in en buiten het huis, zodat de theorie tot de verbeelding gaat spreken. Dan weet je zeker dat je kind alles veel beter onthoudt!

1. Het metriek stelsel is internationaal

Wanneer je iets meet, maak je gebruik van het metriek stelsel. Dat is een afgesproken systeem. Als je een afstand wilt meten, gebruik je daarvoor bijvoorbeeld meters of centimeters.

Een Nederlandse meter is precies even lang als een Zweedse meter. Dat komt omdat het metriek stelsel een internationaal afgesproken systeem is.

De meeste landen in de wereld maken gebruik van hetzelfde metrieke stelsel, het SI-stelsel. 1 van de uitzonderingen is Amerika. Dit land gebruikt bijvoorbeeld geen kilometers, maar mijlen. En geen kilogrammen, maar ‘stone’ en ‘pounds’.

Jouw kind leert op school ook dit veelgebruikte SI-stelsel. Hij krijgt in dat stelsel te maken met grammen, liters en meters.

2. Bij het metriek stelsel hoort altijd een trap

Wist je dat verschillende metrieke stelsels kunnen worden weergegeven als trap?

We geven het metriek stelsel van de lengtematen als voorbeeld. Dat ziet er zo uit:

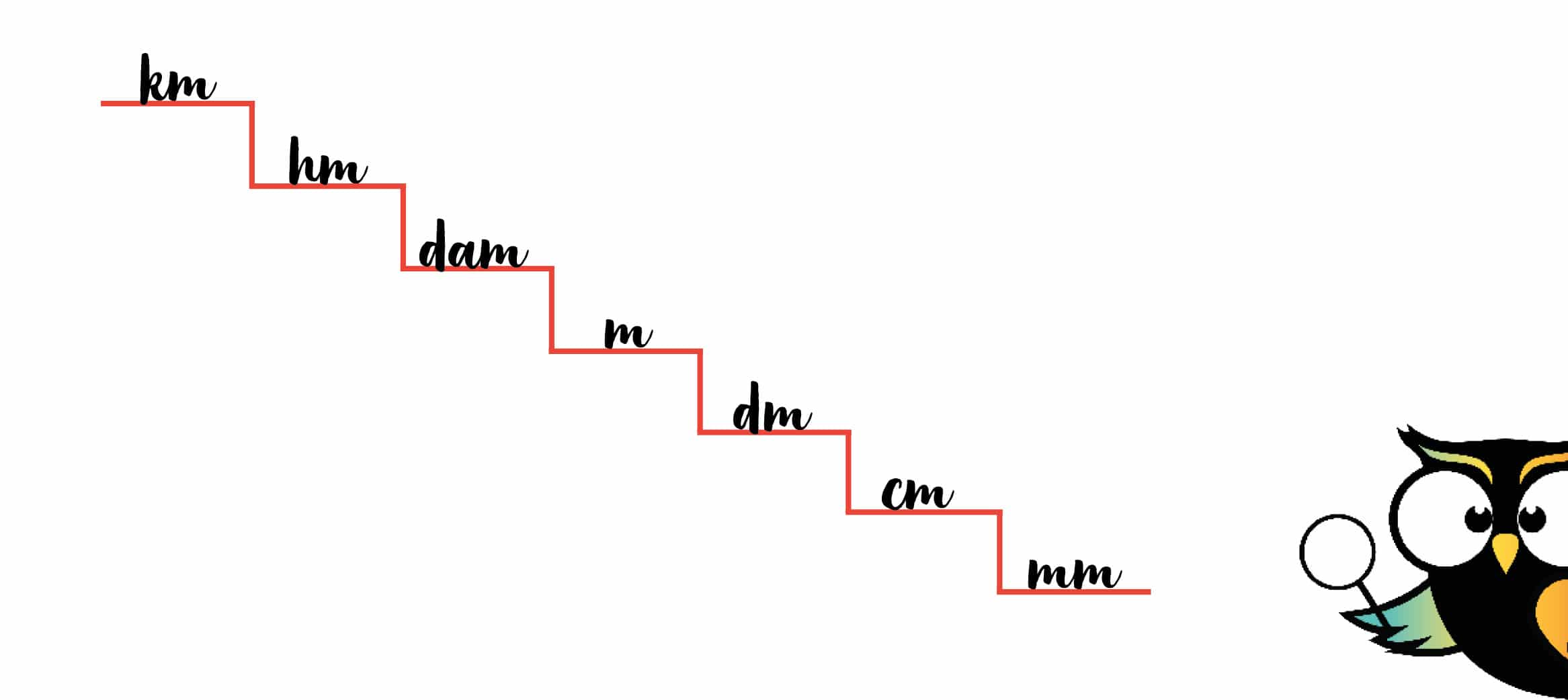
Op de trap zie je allerlei afkortingen staan. Van boven naar beneden zie je:

• km = kilometer
• hm = hectometer
• dam = decameter
• m = meter
• dm = decimeter
• cm = centimeter
• mm = millimeter

De kilometer is op deze trap het grootst, de millimeter het kleinst. Als je deze volgorde niet goed kunt onthouden, kun je het volgende ezelsbruggetje gebruiken:

Kan het dametje met de centimeter meten?

De beginletters van deze zin geven de volgorde van de trap weer.

Als je deze trap naar beneden toe volgt, dus van links naar rechts, doe je bij elke stap die je maakt de afstand x 10.

1 kilometer is dan 1 x 10 = 10 hectometer.

10 hectometer = 10 x 10 = 100 decameter enz.

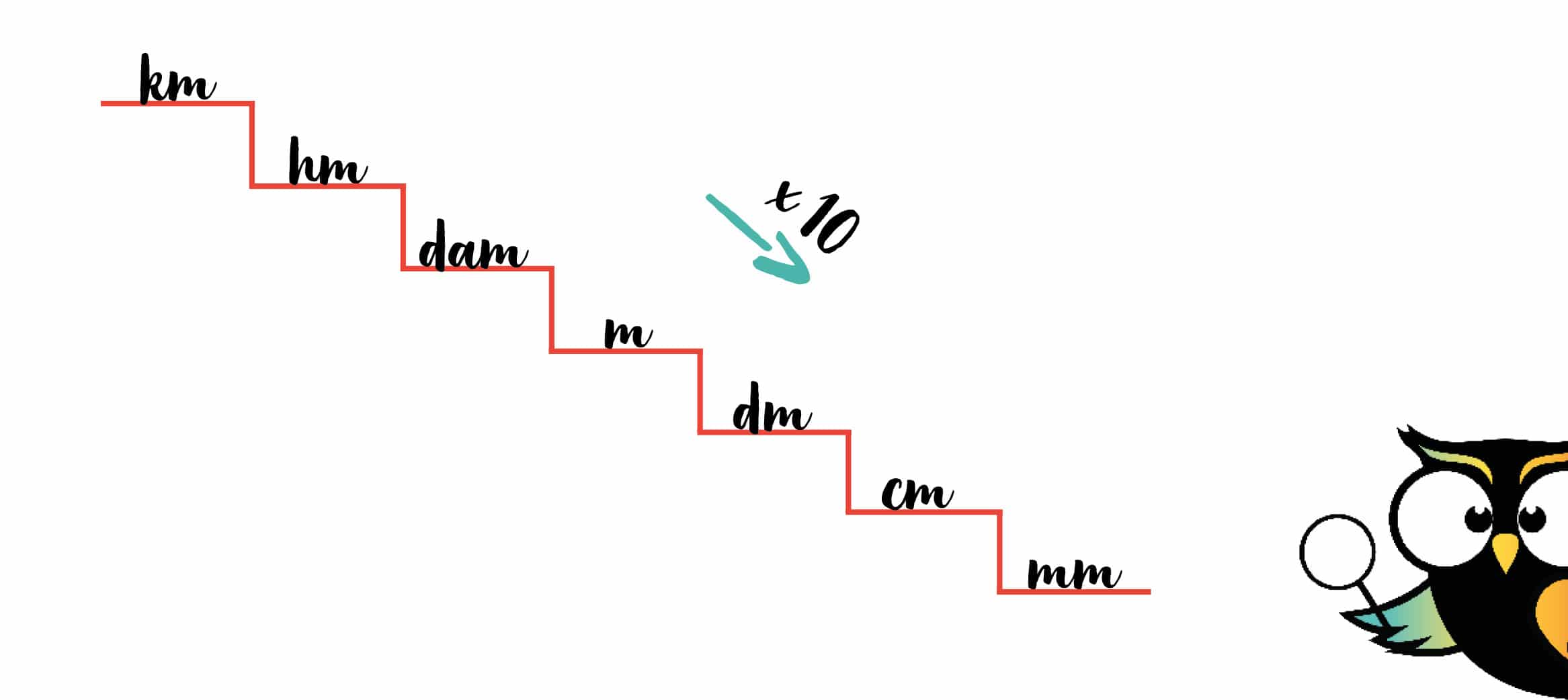
Ga je andersom, dus van rechts naar links de trap op, dan deel je het getal steeds door 10.

100 centimeter is 100 : 10 = 10 decimeter.

10 decimeter is 10 : 10 = 1 meter enz.

Een vergelijkbare trap kun je ook voor de andere metrieke stelsels inzetten, bijvoorbeeld voor de liters of grammen. Maar let op: de ‘m’ van meter verandert dan in de ‘l’ van liter of de ‘g’ van gram:

• kilometer (km) wordt kiloliter (kl) of kilogram (kg)
• hectometer (hm) wordt hectoliter (hl) of hectogram (hg)
• decameter (dam) wordt decaliter (dal) of decagram (dag)
• meter (m) wordt liter (l) of gram (g)
• decimeter (dm) wordt deciliter (dl) of decigram (dg)
• centimeter (cm) wordt centiliter (cl) of centigram (cg)
• millimeter (mm) wordt milliliter (ml) of milligram (mg)

Welke van deze trappen je ook gebruikt; de stappen blijven hetzelfde:

• 1 omlaag (naar rechts) = x 10
• 1 omhoog (naar links) = : 10

Als je moeite hebt dit te onthouden, bedenk dan dit:

• naar rechts —> keer 10
• naar links —> delen door 10

De ‘r’ en de ‘l’ van ‘rechts’ en ‘links’ verraden dus mooi wat je moet doen!

Oefenbladen Rekenen Groep 5 (Gratis)

Download

Oefenbladen Rekenen Groep 6 (Gratis)

Download

3. Oppervlakte en inhoud: m² en m³

Bij meten op de basisschool krijgt je kind ook te maken met de berekening van de oppervlakte en de inhoud.

Oppervlakte

Je ziet boven de ‘m’ bij oppervlakte een 2 staan. En als je de inhoud meet, staat boven die ‘m’ zelfs een 3. Hoe zit dat eigenlijk?

Een oppervlakte wordt weergegeven in vierkante meters (m²). Je geeft dus eigenlijk aan uit hoeveel vierkantjes een bepaald vlak bestaat.

Laten we eens kijken naar een voorbeeld:

De tuin van Dirk is 5 meter lang en 4 meter breed. Bereken de oppervlakte van deze tuin.

De vraag is dus eigenlijk: uit hoeveel vierkanten van 1 m x 1 m bestaat deze tuin? 1 m x 1 m kun je ook schrijven als 1 m²; 1 vierkante meter dus.

Om de oppervlakte te berekenen, reken je de volgende som uit: lengte x breedte. In ons voorbeeld wordt dat dus:

5 x 4 = 20

De oppervlakte van de tuin van Dirk is dus 20 m² (20 vierkante meter). Vergeet niet de m² erbij te zetten. Anders weet je niet waar je antwoord naar verwijst.

Inhoud

Wanneer je de inhoud van iets berekent, wil je weten hoeveel erin past. Je kunt bijvoorbeeld uitrekenen hoeveel water er in een aquarium past.

Inhoudsmaten zien er zo uit: ml³, dm³. Er staat steeds een 3 boven de eenheid.

Dat is niet zo raar als je deze 3 vergelijkt met de 2 van de vierkante meters.

Als je een oppervlakte berekent, doe je lengte x breedte. Je vermenigvuldigt dus 2 afmetingen. Bij een inhoud vermenigvuldig je er 3. Je doet namelijk lengte x breedte x hoogte. De uitkomst wordt gegeven in kubieke meters (of kubieke liters).

Een voorbeeld:

Het aquarium van Tonja heeft een lengte van 3 dm, een breedte van 2 dm en een hoogte van 2 dm. Wat is de inhoud van dit aquarium?

Om de inhoud te berekenen, doe je lengte x breedte x hoogte. Dat wordt:

3 x 2 x 2 = 12

Nu je de uitkomst hebt, kijk je naar de eenheid die erachter moet. Alle afmetingen waren in dm. Dat betekent dat je die sowieso achter de uitkomst zet: 12 dm.

Maar let op: je uitkomst is nog niet klaar. Omdat je 3 afmetingen met elkaar hebt vermenigvuldigd, moet je de 3 nog achter ‘dm’ plaatsen.

Het aquarium van Tonja heeft dus een inhoud van 12 dm³.

Let op: de trappen van oppervlaktematen en inhoudsmaten werken anders dan de trap van de normale maten. In ons artikel over het metriek stelsel leggen we je uit wat het verschil is.

4. 1 liter = 1 dm³

Soms wordt aan je kind gevraagd om bepaalde maten om te rekenen. Bijvoorbeeld in deze som:

De inhoud van een koekblik is 1 dm³. Hoeveel liter is dat?

Het is belangrijk dat je kind begrijpt hoe je van de ene trap naar de andere gaat. En daarvoor is dit weetje superhandig:

1 liter is hetzelfde als 1 dm³!

Dat wil dus zeggen dat je het beste de eenheden eerst kunt omrekenen naar liters (l) of kubieke decimeters (dm³). Vanaf daar is de overstap naar de andere trap helemaal niet meer moeilijk.

Een voorbeeld:

Hoeveel deciliter past er in 1000 cm³?

Je weet dat 1 liter hetzelfde is als 1 dm³.

1000 cm³ is hetzelfde als 1 dm³.

1 dm³ is 1 liter.

1 liter is hetzelfde als 10 deciliter.

In 1000 cm³ past dus 10 deciliter!

Als je de trappen van de verschillende metrieke stelsels goed kent én onthoudt dat 1 liter hetzelfde is als 1 dm³, kun je dit soort sommen vrij gemakkelijk uitrekenen.

5. Symmetrie en spiegelbeeld hebben veel met elkaar te maken

Alle weetjes die we tot nu toe hebben behandeld, horen bij het onderdeel ‘meten’. Dit laatste weetje wijkt daarvan af: het hoort bij de meetkunde.

Al vanaf de onderbouw krijgt je kind te maken met symmetrie. Dat is nogal een lastig woord. Maar wist je dat symmetrie en spiegelbeeld heel veel met elkaar te maken hebben? Als je kind dit weet, worden vragen over symmetrie ineens een stuk makkelijker.

De leerkracht vraagt bijvoorbeeld welke figuur symmetrisch is weergegeven. Je kind hoeft dan alleen maar te kijken welke figuur 2 gelijke kanten heeft die in spiegelbeeld tegen elkaar staan.

Rekenen meten en meetkunde oefenen

Sommen die met meten en meetkunde te maken hebben, kun je het beste regelmatig oefenen. Vooral als je kind de materie lastig vindt. Dat kan thuis, in praktische situaties. Meet bijvoorbeeld samen eens op hoe groot de keukentafel is. Of kijk hoe 100 ml melk eruitziet in een maatbeker, om de melk daarna te gebruiken in een heerlijk recept.

Dit soort opdrachten zijn niet alleen leerzaam, maar ook heel leuk. Samen met je kind ontdek je de wereld van meten en meetkunde.

Wil je daarnaast graag dat je kind op een schoolse manier oefent met opgaven over meten en meetkunde? Dan kun je gebruik maken van de gratis werkbladen van Wijzer over de Basisschool. Je downloadt ze onderaan dit artikel.

Al met al heeft je kind nog zijn hele leven lang te maken met meet- en meetkunde-opdrachten. Ga er dus vooral samen mee aan de slag en kies een manier die bij jullie past!

Bekijk ook:

• Schaal berekenen
• Omtrek berekenen
• Km naar m omrekenen

Judith Kimenai, BEd

Judith was jarenlang docente Nederlands en (tweetalig) biologie binnen het voortgezet onderwijs. Tijdens haar onderwijscarrière was ze naast docente ook een bevlogen brugklasmentor en intern begeleider. Tegenwoordig is Judith freelance tekstschrijfster en richt ze zich voornamelijk op de educatieve sector.

Over Judith