Schaal berekenen, hoe doe je dat? Hier vind je uitleg en kun je oefenen

Heb je wel eens van ‘schaal berekenen‘ of rekenen op schaal gehoord? Als je deze blog gelezen hebt, weet je alles over dit onderwerp. Ook leer je hoe berekeningen met schaal werken.

Klik hier voor meer over het metriek stelsel.

We zetten alle dingen die je leert eerst voor je op een rijtje:

• Je weet wat ‘op schaal rekenen’ betekent.
• Je kunt berekenen hoe groot iets op schaal moet zijn als je de werkelijke grootte en de schaallijn kent.
• Je kunt iets dat op schaal is naar zijn werkelijke grootte terugrekenen.
• Je leert hoe je een verhoudingstabel gebruikt bij schaalberekeningen.
• Je leert hoe je de oppervlakte berekent van een figuur dat op schaal getekend is.
• Je weet hoe de schaallijn van een plattegrond werkt.

Oefenbladen Rekenen Groep 5 (Gratis)

Download

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

Schaal berekenen, wat is dat?

Maar laten we bij het begin beginnen. Wat betekent het eigenlijk als je ‘op schaal rekent’?

Stel, je meester vraagt je een tekening te maken van jouw huis. Dan heb je wel heel veel papier nodig om het op ware grootte te tekenen. Dat is niet zo handig. Daarom teken je je huis veel kleiner.

Je tekent het op schaal.

Ben je wel eens in Madurodam geweest? Daar zijn heel veel belangrijke plekken in de wereld in het klein nagemaakt. Op schaal dus. Ook modelautootjes en souvenirbeeldjes van de Eiffeltoren zijn op schaal gemaakt.

Een tekening op schaal kan ook een tekening zijn waarop iets juist groter is afgebeeld dan het in werkelijkheid is. Denk maar aan de uitvergroting van een vlo.

Op school leer je hoe je dingen op schaal berekent. Je vraagt je misschien af waarom je dat moet leren. Als je naar het voorbeeld van je huis kijkt, begrijp je het waarschijnlijk al. Het is vaak erg handig om iets in het klein te kunnen tekenen of hebben.

Hetzelfde geldt voor verzamelingen. Als jij fan bent van mooie auto’s, wil je er het liefst zo veel mogelijk hebben. Maar echte auto’s zijn wel heel erg duur. Bovendien passen ze niet in je slaapkamer. De kleine schaalmodellen nemen een stuk minder ruimte in beslag en zijn ook nog eens betaalbaar!

Ook als mensen gebouwen ontwerpen, werken ze op schaal. Want stel je voor dat ze het ontwerp van een wolkenkrabber op ware grootte moesten tekenen…

Het is dan wel heel belangrijk dat alles in de juiste verhouding wordt getekend. Als één raam van de wolkenkrabber in werkelijkheid bijvoorbeeld twee keer zo groot is als een ander raam, moet dat op de tekening ook zo zijn.

Nu je weet wat ‘op schaal rekenen’ betekent, is het tijd voor de volgende stap. Je gaat nu leren hoe rekenen op schaal werkt. En dat is handig, omdat deze opgaven ook vaak voorkomen in de vorm van verhaaltjessommen in toetsen.

Bekijk ook:

• Metriek stelsel oefenen en uitleg
• Maten omrekenen: een handig ezelsbruggetje
• Meten en meetkunde: 5 handige weetjes
• Inhoud berekenen: hoe ga je van liter naar dm3?
• Km naar m omrekenen
• Oppervlakte berekenen
• Omtrek berekenen
• Kan het dametje met de centimeter meten: een handig ezelsbruggetje

Hoe bereken je de schaal?

We laten je nu met wat voorbeelden zien hoe een berekening op schaal werkt. Eerst kijken we naar een som waarbij het dier op de tekening kleiner is dan het in werkelijkheid is. Daarna geven we een voorbeeld van een dier dat op de tekening groter is dan in het echt.

Van klein naar groot

Je ziet hieronder een tekening van een olifant. Deze olifant is natuurlijk kleiner gemaakt. Een echte olifant, op ware grootte, past niet op het blaadje. De olifant is dus op schaal getekend.

Onder de tekening zie je een streep staan. Die streep noem je de schaallijn. Met behulp van die lijn kun je precies uitrekenen hoe groot de olifant in het echt is.

Je ziet dat bij de schaallijn een maat staat geschreven. Er staat dat de lengte van de lijn op het blaadje in het echt 1 meter is. Als je de lijn op het blaadje met een liniaal nameet, zie je dat hij 2 centimeter lang is.

Dat betekent het volgende: 2 centimeter op het blaadje is hetzelfde als 1 meter in het echt.

Nu meet je de olifant op het blad. Die is 6 centimeter. De schaallijn past daar precies 3 keer in. Je kunt dat berekenen door 6 (de grootte van de olifant) te delen door 2 (de grootte van de schaallijn).

Je weet vast nog dat 1 schaallijn in het echt 1 meter is. Dus als je 3 schaallijnen nodig hebt om de lengte van deze olifant te meten, weet je dat de olifant 3 x 1 = 3 meter lang is. Wat een enorm dier!

Van groot naar klein

Maar het kan ook andersom.

Kijk maar naar deze poster van een schattige hamster. Op de poster is de hamster natuurlijk veel groter dan in het echt. Ik wil graag weten hoe groot het diertje in het echt is.

Gelukkig staat er ook op deze poster een schaallijn. Zonder schaallijn zou ik alleen maar kunnen raden hoe groot deze hamster in het echt is. Nu kan ik het berekenen.

Bij de schaallijn staat dat hij in het echt 1 centimeter is. Als we hem opmeten, zien we dat hij op de poster 5 centimeter is. Dat betekent het volgende: 5 centimeter op de poster is hetzelfde als 1 centimeter in het echt.

De volgende stap is opmeten hoe groot de hamster op de poster is. Als we er een liniaal langs leggen, meten we 25 centimeter.

Nu pakken we de schaallijn er nog eens bij. Die is in het echt 1 centimeter, terwijl hij op de poster 5 centimeter is. Omdat onze hamster ook op de poster staat, berekenen we hoe vaak de schaallijn van de poster in deze hamster past. We delen daarom 25 door 5. De uitkomst is 5.

Nu weten we dat de hamster in het echt geen 25 centimeter is (stel je voor!), maar 5 centimeter. Als je wel eens een echte hamster hebt gezien, weet je dat dat best kan kloppen.

Werken met een verhoudingstabel

Je weet nu wat het betekent als je moet rekenen op schaal. Ook weet je hoe je de ware grootte van een verkleind of vergroot dier of ding kunt uitrekenen.

Maar wist je dat je de schaal ook kunt berekenen met een verhoudingstabel? We leggen je nu uit hoe dat werkt.

Een schaalmodel is een exacte kopie van het origineel. Maar dan in een andere maat. Meestal is dat een verkleining. Alle onderdeeltjes moeten ook in het klein het juiste formaat krijgen. Met andere woorden: ze moeten in de juiste verhouding staan. Denk maar aan het voorbeeld van de ramen in de wolkenkrabber. Met behulp van een verhoudingstabel kun je van alle onderdelen van je tekening de juiste maten uitrekenen.

We kijken nu naar een paar andere voorbeelden. Eerst weer eentje waarbij we een tekening van een auto naar ware grootte berekenen (van klein naar groot dus).

Daarna doen we het weer andersom: we gebruiken de verhoudingstabel om de ware grootte van een mug te berekenen. De tekening van de mug is groter dan de mug zelf, dus we werken van groot naar klein.

Van klein naar groot

Als eerste deze getekende auto.

Onder de auto staat dat de auto op de tekening 8 centimeter is. En dat de schaal 1 op 60 is. Als de schaal 1 op 60 is, betekent dat dat 1 centimeter op papier in het echt 60 centimeter is.

We zetten deze getallen nu in een verhoudingstabel. Je tekent eerst een lege tabel.

Daarna vul je in wat je al weet. In het geval van de auto weet je dat 1 centimeter op de tekening in het echt 60 centimeter is. Zet de 1 in het bovenste vakje en de 60 er precies onder.

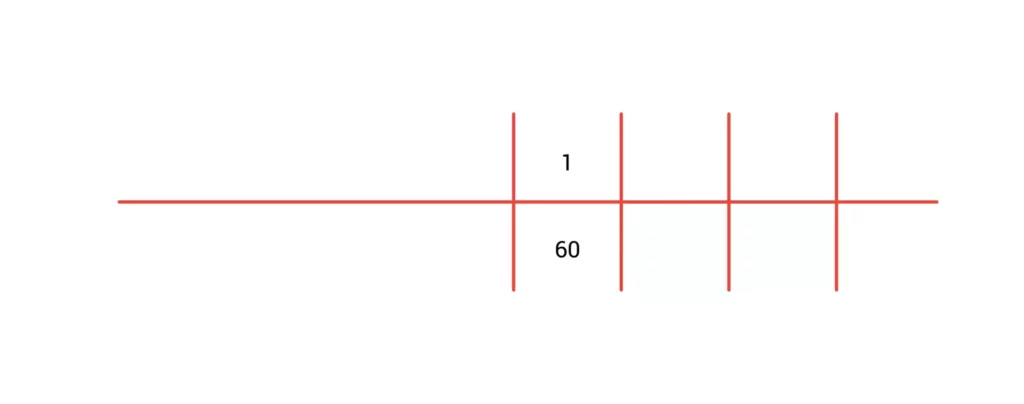
Je kunt nu ook de woorden invullen aan de linkerkant van de tabel.

Voor de 1 zet je ‘afmeting tekening in cm’.
Voor de 60 zet je ‘afmeting werkelijkheid in cm’.

Je weet ook dat de auto op de tekening 8 centimeter is. De 8 schrijf je ook op, naast de 1. Je weet nog niet hoe groot de afmeting van de auto in werkelijkheid is, dus in het vakje onder de 8 zet je een vraagteken.

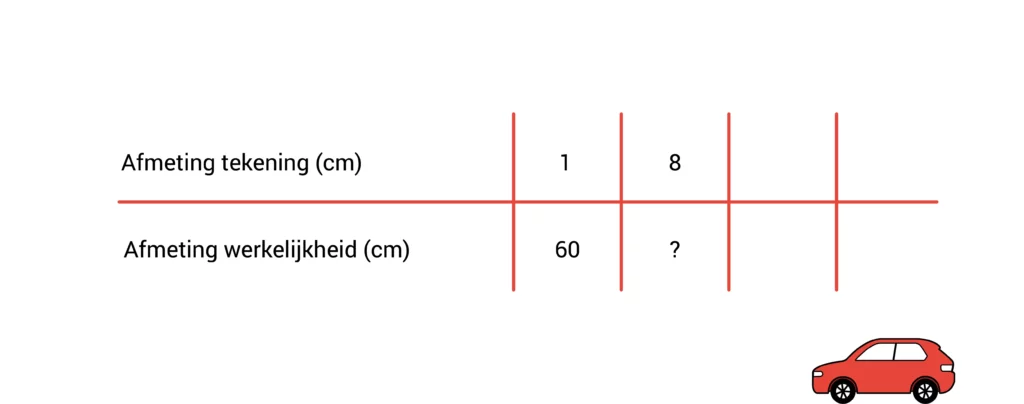
Bij een verhoudingstabel werkt het altijd zo: wat je aan de bovenkant doet, doe je aan de onderkant ook.

Aan de bovenkant ben je van 1 centimeter naar 8 centimeter gegaan. Je hebt dus de 1 keer 8 gedaan, ofwel 8 keer groter gemaakt. Dat betekent dat je dat aan de onderkant nu ook moet doen.

Onder 1 centimeter staat 60 centimeter. Je doet nu 60 x 8. De uitkomst van die som is 480. 8 centimeter op de tekening is dus hetzelfde als 480 centimeter in werkelijkheid. De auto is in het echt dus 480 centimeter lang.

Met de trap uit het metriek stelsel kun je de 480 centimeter omrekenen naar meters.

480 centimeter = 48 decimeter
48 decimeter = 4,8 meter

De auto is in het echt dus 4 meter en 80 centimeter.

Van groot naar klein

Zoals gezegd kunnen we ook met een verhoudingstabel van groot naar klein rekenen. We gebruiken daarvoor deze tekening van een mug.

De mug op de tekening is 98 millimeter lang. De schaal die erbij staat is 7 : 1. Dat betekent dat 7 millimeter op het papier in het echt 1 millimeter is.

Om te berekenen hoe groot de mug in werkelijkheid is, gebruiken we een verhoudingstabel. Daarin vullen we weer in wat we weten:

• In het eerste vakje boven zetten we ‘afmeting tekening in mm’.
• In het vakje daaronder zetten we ‘afmeting werkelijkheid in mm’.
• In het eerste kleine vakje beneden zetten we 1 mm.
• In het vakje daarboven zetten we 7 mm. We weten namelijk dat 1 mm in werkelijkheid hetzelfde is als 7 mm op de tekening.
• Naast de 7 zet ik 98, omdat ik weet dat de mug op de tekening 98 mm is.
• Onder de 98 zetten we een vraagteken. We weten namelijk nog niet hoe groot de mug in werkelijkheid is.

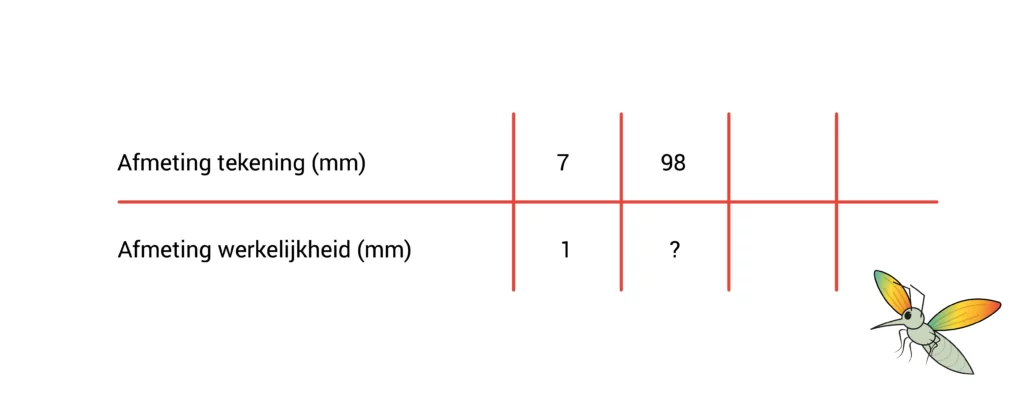
We gaan nu bekijken wat we moeten doen om van 7 naar 98 te komen. Daarvoor moet je weten hoeveel keer 7 past in 98. Je kunt daarvoor 98 delen door 7. Dat is in één keer best lastig. Daarom berekenen we de uitkomst via tussenstapjes.

Als je eerst de 7 10 keer zo groot maakt, krijg je 70.

Nu houd je nog 28 millimeter over (98 – 70). 7 past 4 keer in 28, want 28 : 7 = 4.

In totaal past 7 dus 10 + 4 = 14 keer in 98! Om van 7 millimeter naar 98 millimeter te komen, vermenigvuldig je 7 met 14.

Hetzelfde doe je nu met het onderste getal. 1 x 14 = 14. Dat is het getal wat je onder 98 schrijft.

Wow! De mug is dan wel 98 millimeter op papier, maar in het echt is hij maar 14 millimeter. Klopt dat wel? Dat is wel heel erg klein. Vergelijk een mug eens met je vingernagel. Die is ongeveer 10 millimeter (1 centimeter). Dat betekent dat de mug iets groter is dan je nagel. Klopt aardig, toch?

Voorbeelden van schaal uitrekenen

We geven je nog wat voorbeelden om te laten zien hoe je met schaal rekent.

Het huis van Joel

Joel heeft zijn huis nagetekend op een vel papier. Hij heeft daarbij heel goed gekeken naar de afmetingen van het huis in werkelijkheid. Onder zijn tekening staat de schaal: 1 : 100.

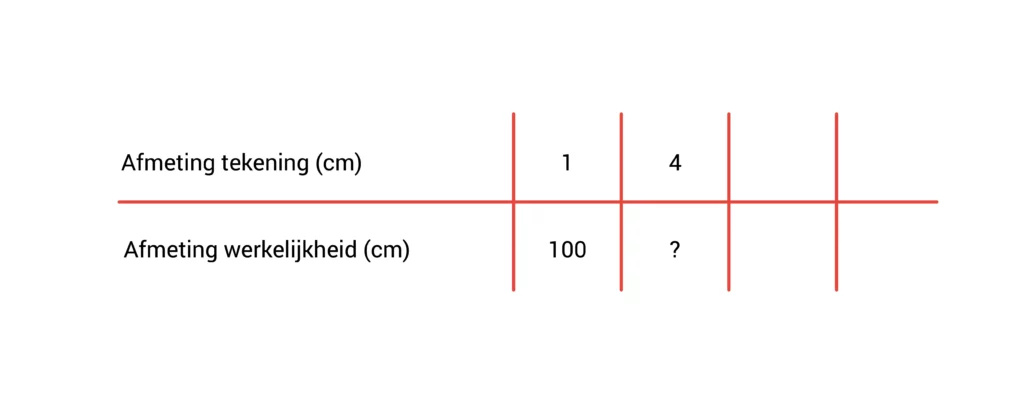
Hoe breed is de voorkant van Joels huis in het echt?

Als de schaal 1 : 100 is, weet je dat 1 centimeter op de tekening hetzelfde is als 100 centimeter in het echt.

Zet deze getallen eerst in een verhoudingstabel. Die ziet er als volgt uit:

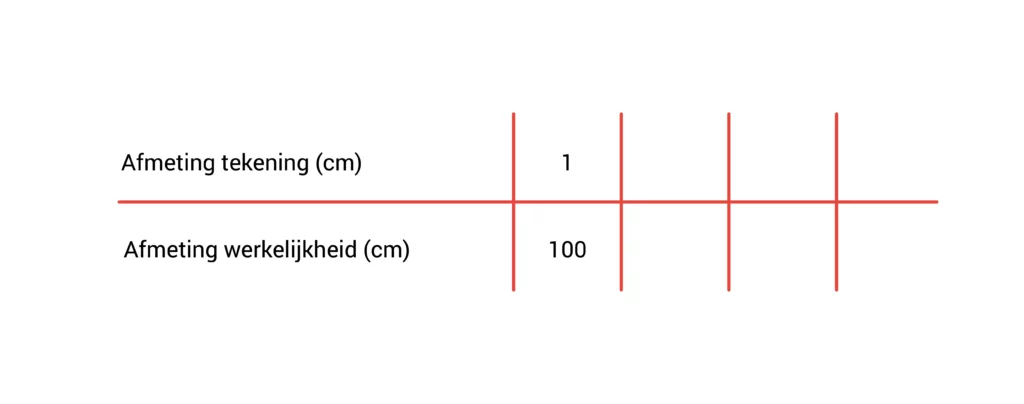
Vervolgens meet je de breedte van het huis op de tekening op. Die is 4 centimeter. Zet de 4 naast de 1. Onder de 4 zet je een vraagteken, want je weet nog niet hoe breed het huis in werkelijkheid is.

Aan de bovenkant ben je van 1 centimeter naar 4 centimeter gegaan. Dat is 1 x 4. Aan de onderkant doe je hetzelfde, maar dan met 100.

100 x 4 = 400

4 centimeter op de tekening is dus hetzelfde als 400 centimeter in werkelijkheid. Het huis is dus 400 centimeter breed. 400 centimeter is hetzelfde als 4 meter.

De breedte van de voorkant van Joels huis is 4 meter.

Een pissebed van formaat

Jinthe heeft in haar tijdschrift over insecten een poster gevonden van een pissebed. Hij is enorm! Ze kan er alle details goed op zien.

Jinthe weet dat een pissebed in werkelijkheid gelukkig niet zo groot is. Ze is wel nieuwsgierig naar zijn ware grootte. Daarom besluit ze die uit te rekenen.

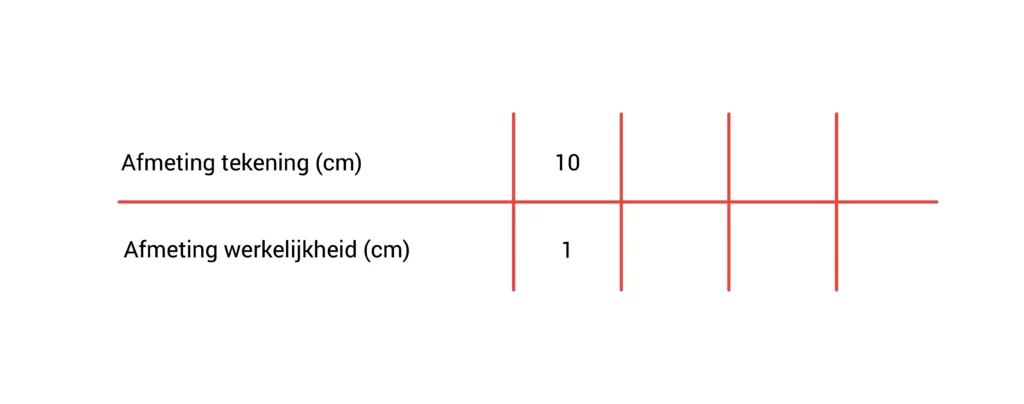
Onder de tekening staat een schaal: 10 : 1. Dat betekent dat 10 centimeter op de tekening hetzelfde is als 1 centimeter in werkelijkheid.

Jinthe begint met het tekenen van een verhoudingstabel. Daar zet ze alle dingen in die ze al weet.

Vervolgens meet Jinthe de pissebed van de poster op. Die is 20 centimeter. Dit getal zet ze naast de 10 in de verhoudingstabel. Onder de 20 zet ze een vraagteken neer, omdat ze nog niet weet hoe groot de pissebed in het echt is.

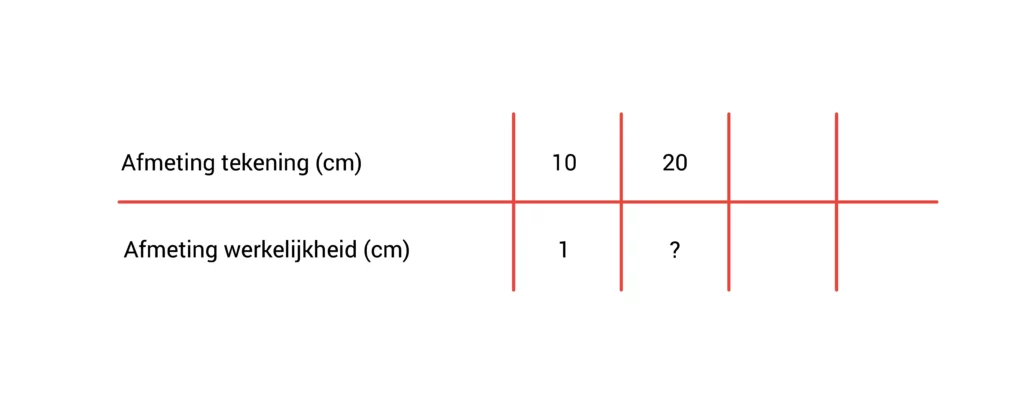
Jinthe weet dat ze aan de bovenkant van de tabel van 10 naar 20 is gegaan. Dat is dus 10 x 2. Nu weet ze dat ze aan de onderkant van de tabel hetzelfde moet doen.

1 x 2 = 2.

Onder de 20 moet dus het getal 2 staan. En daar hebben we meteen ons antwoord op de vraag hoe groot de pissebed in werkelijkheid is: 2 centimeter!

Oppervlakte met schaal berekenen

Ben je klaar voor een uitdaging? We gaan nu namelijk kijken hoe je de oppervlakte berekent van een figuur als je tekening niet op ware grootte is! Dat gaan we doen met behulp van een voorbeeld.

Dylan is verhuisd. Hij krijgt een nieuw huis met een tuin die hij nog nooit goed heeft bekeken. Dylan heeft wel een tekening op schaal van de tuin.

Hij wil voor de hele tuin kunstgras gaan bestellen. Om uit te rekenen hoeveel kunstgras hij nodig heeft, gebruikt hij de tekening.

Tekening van een groen vlak met schaal eronder: 1 : 150

De lengte van de tuin op de tekening 4 centimeter. De breedte is 2 centimeter.

De oppervlakte van de tuin op de tekening rekenen we uit met lengte x breedte.

Dat is dus 4 x 2 = 8 cm².

Maar een tuin van 8 cm² is in werkelijkheid wel heel klein! Om de oppervlakte van de echte tuin uit te rekenen, moet Dylan eerst iets anders doen.

Voordat hij de oppervlakte berekent met lengte x breedte, moet Dylan de lengte en de breedte in werkelijkheid weten.

De lengte van de tuin is op de tekening 4 centimeter. Dylan weet dat de schaal 1 : 150 is. 1 centimeter in werkelijkheid is dus 150 centimeter in het echt.

4 x 150 = 600 centimeter. Dat is hetzelfde als 6 meter.

Voor de breedte doet Dylan hetzelfde:

2 x 150 = 300 centimeter. Dat is hetzelfde als 3 meter.

Nu Dylan weet wat de werkelijke afmetingen zijn, kan hij de oppervlakte van de echte tuin berekenen. Dat doet hij op dezelfde manier: lengte x breedte.

6 x 3 = 18

De oppervlakte van Dylans nieuwe tuin is 18 m².

Schaal van kaart berekenen

Laten we nu eens naar plattegronden kijken. Op een kaart of plattegrond zie je ook de werkelijkheid in het klein. Dit is bijvoorbeeld de kaart van Nederland. Nederland staat hier in het klein op. Op schaal dus.

De schaal kun je vinden op de schaallijn. Deze kaart heeft een schaal van 1 op 2.500.000. Ook hier zie je hoe dat wordt geschreven:

Schaal = 1 : 2.500.000.
1 centimeter op deze kaart is dus 2.500.000 centimeter in het echt.

Als je de afstand zou meten tussen Amsterdam en Rotterdam op deze kaart, kun je berekenen hoeveel kilometer die twee steden van elkaar vandaan liggen.

Je meet daarvoor de lijn tussen Amsterdam en Rotterdam. Die lijn is volgens de liniaal 3 centimeter. Door de schaallijn weet je dat 1 centimeter op de kaart hetzelfde is als 2.500.000 centimeter in werkelijkheid.

Dat betekent dat Amsterdam in het echt 3 x 2.500.000 cm van Rotterdam af ligt. Dat is dus 3 x 25 = 75, met nog 5 nullen erachter: 7.500.000 centimeter.

Het is moeilijk in te schatten of dit een grote afstand is. 7.500.000 centimeter zegt ons namelijk niet zoveel. Daarom moet je dit getal eerst nog even omrekenen naar kilometers.

Je gebruikt daarvoor de trap van het metriek stelsel. Van centimeters naar kilometers is naar links op de trap. Dat betekent dat je gaat delen.

Eerst ga je van centimeters naar decimeters, dan naar meters, decameters, hectometers en pas daarna kom je uit op kilometers. Je moet het getal dus 5 x door 10 delen. 5 nullen eraf dus!

7.500.000 centimeter is dus hetzelfde als 75 kilometer. Van Amsterdam naar Rotterdam is de afstand dus 75 kilometer.

Nu je alles weet van de schaal en ook weet hoe je sommen met schaal berekent, geven we je een overzicht van de momenten waarop je leert over dit onderwerp.

Schaal berekenen groep 7

Hoewel je er in groep 6 waarschijnlijk al mee bezig bent geweest, leer je in groep 7 de schaal pas echt goed kennen. Deze dingen kun je verwachten in groep 7.

Je leert…

• een schaalnotatie (bijvoorbeeld 1 : 30) of schaallijn herkennen.
• hoe je een schaalnotatie uitspreekt, bijvoorbeeld als ‘1 op 30’.
• wat het betekent als ergens ‘1 : 30’ staat.
• rekenen met schaallijnen en schaalnotaties in simpele situaties.

Schaal berekenen groep 8

In groep 8 blijf je uiteraard oefenen met de dingen uit groep 7. Daarnaast leer je:

• rekenen met schaallijnen en schaalnotaties in moeilijkere situaties (lastige getallen).
• hoe je de oppervlakte berekent van een rechthoekige figuur dat is afgebeeld op schaal.

Dit was alles wat we je over schaal en schaalberekeningen wilden vertellen. Je hebt nu geleerd…

• wat ‘op schaal rekenen’ betekent.
• hoe je iets op ware grootte tekent met de juiste afmetingen op schaal.
• hoe je iets dat op schaal is naar zijn werkelijke grootte terugrekent.
• hoe je een verhoudingstabel gebruikt bij schaalberekeningen.
• hoe je de oppervlakte berekent van een figuur dat op schaal getekend is.
• hoe de schaallijn van een plattegrond werkt.

Wil je graag zelf oefenen? Kijk dan eens hieronder. We hebben speciaal voor jou een aantal opgaven op een rijtje gezet. De antwoorden van de opgaven vind je helemaal onderaan op de pagina.

Wat vind jij van schaalberekeningen? We zijn benieuwd naar je mening!

Schaal berekenen oefeningen

Opdracht 1

Juul ziet een plattegrond van haar woonplaats. Onderaan de plattegrond staat de schaalnotatie: 1 : 25.000. De afstand tussen Juuls huis en haar school is op de kaart 4 centimeter. Hoe ver woont Juul van haar school af in kilometers?

Opdracht 2

Pim wil een uitvergrote tekening maken van een echte mier. De echte mier is 12 millimeter lang. De schaal van de tekening is 30 : 1 (mm). Hoeveel centimeter moet de mier op de tekening zijn?

Opdracht 3

Janna wil weten hoe lang een op schaal getekende auto in het echt is. D

e schaal van de tekening is 1 : 85. Het autootje op de tekening is 5 centimeter lang. Hoe lang is de auto in het echt?

Antwoord opdracht 1

1 centimeter op de kaart is 25.000 centimeter in werkelijkheid.
4 centimeter op de kaart is 4 x 25.000 = 100.000 centimeter.

100.000 centimeter = 1 kilometer.

Juul woont dus 1 kilometer van haar school af.

Antwoord opdracht 2

1 millimeter in het het echt is 30 millimeter op de tekening.
De mier is in het echt 12 millimeter lang. Dat is dus 12 x 30 = 360 millimeter op de tekening.

360 millimeter is hetzelfde als 36 centimeter.

Het antwoord op de vraag is dus 36 centimeter.

Antwoord opdracht 3

1 centimeter op de tekening komt overeen met 85 centimeter in het echt.

5 centimeter op de tekening is dus 5 x 85 = 425 centimeter in het echt.

425 centimeter is hetzelfde als 4,25 meter.

De auto is dus 4,25 meter lang.

Rochelle Schaepkens, BEd Master EN

Rochelle behaalde een Bachelor en Master of Education (PABO en Master Leren en Innoveren). Daarnaast heeft ze de opleidingen tot Taalexpert, Rekenexpert en Remedial Teaching gevolgd. Ze heeft 20 jaar ervaring als leerkracht en unitleider op een basisschool. Nu werkt ze als docent op de Pabo en als Content Creator voor Wijzer over de basisschool.

Over Rochelle