Tafelkaart printen als hulpmiddel (met 8 pdf-tafelkaarten)

Ken jij de tafelkaarten al? Op een tafelkaart staan de tafels en meestal ook de antwoorden die daarbij horen. In dit artikel vind je de meestgebruikte tafelkaarten als pdf. Die zijn natuurlijk ontzettend handig als je rekenen wilt oefenen. Download en print alle tafelkaarten hier gratis!

Tafelkaart tot en met 10

Er zijn verschillende soorten tafelkaarten:

1. Een tafelkaart met rijtjes keersommen naast en onder elkaar

Bijvoorbeeld:

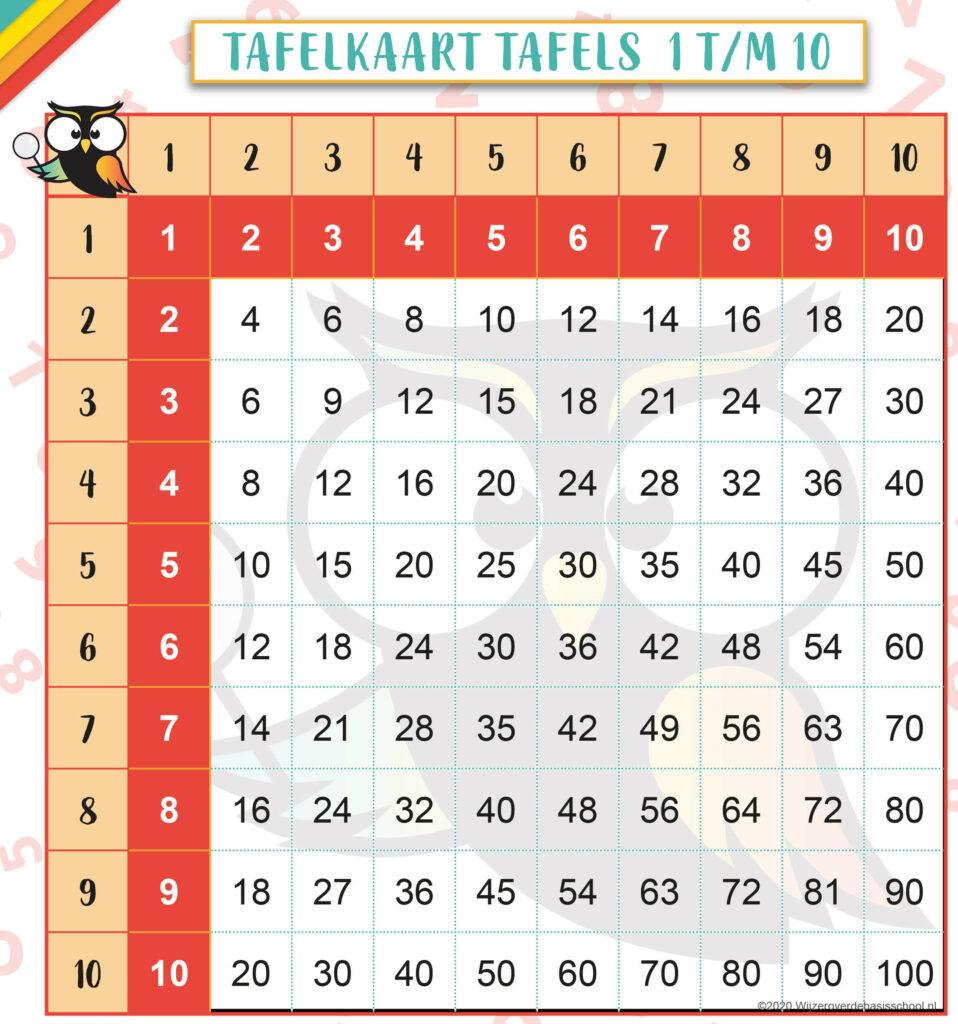
2. Een tafelkaart met getallen op een horizontale lijn en op een verticale lijn

Bijvoorbeeld:

Stappenplan voor het gebruik van deze tafelkaart

• Je wilt de som 4 x 8 = uitrekenen.
• Ga met een vinger van je linkerhand op de 4 staan in de eerste kolom (de verticale as).
• Ga met een vinger van je rechterhand op de 8 staan in de eerste rij (de horizontale as).
• Beweeg de 2 vingers naar elkaar toe.
• Je vingers komen elkaar tegen op het getal 32. Dit is het antwoord op je vraag: 4 x 8 = 32.

Deze tafelkaart heeft alle antwoorden van de tafels 1 tot en met 10 in een handig schema staan. Dat is natuurlijk erg fijn als je de tafels wilt oefenen. Je kunt de tafelkaart natuurlijk uitbreiden met de tafels 11 en 12, of zelfs met nog meer tafels.

3. Een tafelkaart waar de sommen met of zonder antwoorden in een schema staan

Bijvoorbeeld:

Wanneer gebruik je een tafelkaart?

Je kunt een tafelkaart gebruiken …

• als je wilt oefenen met het automatiseren van de tafels.
  Doordat je kind de sommen en de antwoorden herhaaldelijk ziet, automatiseert het deze sommen sneller.
• als je kind de moeilijke tafels moet leren.
  Voor kinderen die moeite hebben met rekenen, is het aanleren van de moeilijke tafels een hele klus. Je kunt dan een lege tafelkaart gebruiken. Daarop zijn de antwoorden van de sommen weggelaten. Je kind vult de antwoorden zelf in. Het begint bij de tafels die het al wel kent. Met behulp van die antwoorden rekent je kind ook de antwoorden van de overige sommen uit.
  
  De tafels die kinderen vaak het moeilijkst vinden, zijn de tafels van 3, 4, 6, 7, 8 en 9. Als je hiermee wilt oefenen, moet je kind tafels van 1, 2, 5 en 10 al beheersen. Deze gebruikt je kind namelijk om de antwoorden van de overige tafels uit te rekenen. De bekende tafels zijn een soort kapstok voor de moeilijke tafels. Als je kind de tafel van 5 kent, kan het bijvoorbeeld ook de som 6 x 3 in stappen uitrekenen. 3 x 5 = 5 x 3 = 15, dus 6 x 3 = 15 + 3 = 18.
  
  De volgende strategieën kun je gebruiken als je kind een (moeilijke) nieuwe tafel aan moet leren:

In onderstaande afbeelding kun je zien hoe je tot nieuwe antwoorden kan komen met behulp van de antwoorden die je al weet.

• voor het controleren van antwoorden. Als je kind twijfelt aan een antwoord, is het fijn als het het antwoord kan controleren. Na een tijdje weet je kind het juiste antwoord zelf en is de tafelkaart niet meer nodig.
• als je kind de tafels nog niet goed heeft geautomatiseerd. Je kind kan hierdoor in de problemen raken als het een som moet maken waarbij de vermenigvuldiging niet de kern is van de som. We leggen je uit wat dat betekent met een voorbeeld.
  
  Bij de som 4 x 5 is de vermenigvuldiging de enige som die je kind moet uitrekenen. De vermenigvuldiging is hier de kern.
  
  Bij een verhaalsom is een vermenigvuldiging vaak slechts een van de bewerkingen om tot het juiste antwoord te komen. De vermenigvuldiging is dan niet de kern van de som. Bijvoorbeeld:
  
  De juf trakteert haar leerlingen op een ijsje. Er zitten 28 leerlingen in haar groep. In een doos ijsjes zitten 8 ijsjes. Een doos ijsjes kost € 3,20. De juf betaalt met een briefje van € 20. Hoeveel krijgt de juf terug?
  
  Je kind rekent eerst uit hoeveel dozen de juf nodig heeft: 3 dozen met 8 ijsjes is te weinig (3 x 8 = 24). Ze heeft dus 4 dozen nodig, want 4 x 8 = 32. Je kind heeft nu al een keersom uitgerekend, maar de som is nog niet opgelost. Om te weten hoeveel geld de juf terugkrijgt, moet je kind eerst uitrekenen hoeveel ze moet betalen. Ook dit is een vermenigvuldiging: 4 x € 3,20 = € 12,80
  
  De juf betaalt met een briefje van € 20: € 20 – € 12,80 = € 7,20.
  Het antwoord op deze som is dus € 7,20.
  
  Om tot dit antwoord te komen, heeft je kind 3 keersommen en een minsom uitgerekend:
  3 x 8 = 24
  4 x 8 = 32
  4 x € 3,20 = € 12,80
  € 20 – € 12,80 = € 7,20
  
  Als je kind de tafels niet goed beheerst, is het waarschijnlijk erg lastig om deze som uit te rekenen. Ook al snapt je kind wel welke stappen er nodig zijn om tot het juiste antwoord te komen. Een tafelkaart kan dan een mooi hulpmiddel zijn.

Stap voor stap tafels leren

In groep 4 en groep 5 biedt de leerkracht de tafels aan. Dit gebeurt in eerste instantie meestal zonder een tafelkaart. Op het moment dat je kind een tafelkaart gaat gebruiken, beheerst het vaak de makkelijke tafels al. Deze tafels kun je op de tafelkaart arceren. Zo blijven alleen de sommen over die je kind nog niet kent.

De meeste kinderen kunnen de tafels van 1, 2, 5 en 10 al snel arceren. Om te laten zien hoe dit werkt, gebruiken we in dit artikel de tafelkaart met de getallen op een horizontale lijn en op een verticale lijn. De tafel van 1 levert meestal geen problemen op. Die kun je van boven naar beneden arceren én van links naar rechts:

De tafel van 10 kennen de meeste kinderen ook. Als dat voor jouw kind ook geldt, kun je deze dus ook arceren:

En als de tafels van 5 en 2 ook geen problemen opleveren, kun je deze natuurlijk ook arceren:

Heeft je kind nog moeite met de tafel van 5? Vertel dan dat de uitkomsten van de tafel van 5 altijd eindigen op een 5 of een 0. Laat dit ook zien: schrijf de tafel en de antwoorden samen op. Als je kind dit weet, leert het deze tafel weer iets makkelijker.

Als je alle bovengenoemde tafels hebt gearceerd, zijn er in totaal al 64 van de 100 vakjes rood. Dit geeft veel kinderen meer zelfvertrouwen. Ze kennen al meer dan de helft!

Trucje voor de tafel van 9

De tafel van 9 leert je kind vaak ook snel, als het de volgende kennis heeft: wanneer je de getallen van de uitkomsten bij elkaar optelt, kom je altijd uit op 9. Kijk maar:

1 x 9 = 9 —> 9
2 x 9 = 18 —> 1 + 8 = 9
3 x 9 = 27 —> 2 + 7 = 9
4 x 9 = 36 —> 3 + 6 = 9
5 x 9 = 45 —> 4 + 5 = 9
6 x 9 = 54 —> 5 + 4 = 9
7 x 9 = 63 —> 6 + 3 = 9
8 x 9 = 72 —> 7 + 2 = 9
9 x 9 = 81 —> 8 + 1 = 9
10 x 9 = 90 —> 9 + 0 = 9

Er is nog een trucje om de tafel van 9 te leren. Als je de uitkomsten onder elkaar zet, zie je dat de tientallen steeds eentje meer worden, terwijl de eenheden steeds eentje minder worden.

Dan zijn er nog de kwadraten. Deze zijn meestal ook wat makkelijker te onthouden, omdat het opvallende sommen zijn.

1 x 1 = 1
2 x 2 = 4
3 x 3 = 9
4 x 4 = 16
5 x 5 = 25
6 x 6 = 36
7 x 7 = 49
8 x 8 = 64
9 x 9 = 81
10 x 10 = 100

Als je de tafel van 9 en de kwadraten ook nog kunt arceren op de tafelkaart, blijven er maar 20 moeilijke sommen over. Die moet je kind nog leren en automatiseren. Maar dat is heel wat minder werk dan 100 sommen!

Bekijk ook:

• Tafels leren groep 4
• Tafels oefenen groep 5 met spelletjes (+ handig ezelsbruggetje) of bestel meteen het oefenboek tafels
• Tafels van vermenigvuldiging spellen (aanbevolen door onderwijsexperts)

Tafels automatiseren

Het automatiseren van de tafels hoort bij de basisvaardigheden van het rekenen. Als je kind de tafels goed beheerst en goed heeft geautomatiseerd, kan het sneller complexere opgaven oplossen. Als dat nog niet het geval is, gaat alle aandacht naar de keersom. Je kind gebruikt dan veel ruimte in het werkgeheugen voor het uitrekenen van de keersom. Er blijft dan onvoldoende ruimte in het werkgeheugen over om de rest van de som uit te rekenen.

Voordat je kind echt gaat vermenigvuldigen, leert het eerst herhaaldelijk optellen. Daarmee maakt je kind al kennis met het principe van een vermenigvuldiging. Eerst oefent je kind met eenvoudige sommen. De termen ‘keersom’ en ’tafel’ komen nog niet aan bod. Bijvoorbeeld:

Hoeveel bananen zie je samen?

De meeste kinderen hebben het antwoord waarschijnlijk nog niet paraat, omdat ze de som 3 x 3 nog niet kennen. Om tot het juiste antwoord te komen, moeten ze de bananen tellen. Het werkgeheugen wordt helemaal in beslag genomen voor het uitrekenen van deze som.

In groep 4 komt je kind voor het eerst in aanraking met de tafels. Je kind leert wat een vermenigvuldiging is en wat een tafel is. Daarnaast gaat het oefenen met kale sommen en verhaalsommen. De kale sommen zijn rijtjes met keersommen. Bijvoorbeeld de tafel van 2:

1 x 2 = …
2 x 2 = …
3 x 2 = …
4 x 2 = …
5 x 2 = …
6 x 2 = …
7 x 2 = …
8 x 2 = …
9 x 2 = …
10 x 2 = …

Daarna biedt de leerkracht de sommen door elkaar aan. Je kind moet ze dan op die manier oefenen. Bijvoorbeeld:

2 x 2 = …
1 x 2 = …
4 x 2 = …
7 x 2 = …
5 x 2 = …
8 x 2 = …
10 x 2 = …
3 x 2 = …
6 x 2 = …
9 x 2 = …

Als je kind de kale sommen beheerst, moet het de stof gaan toepassen in verhaalsommen. Bijvoorbeeld:

De bloemist heeft 26 tulpen. In ieder boeket dat hij maakt, gaan 4 tulpen. De bloemist maakt 6 boeketten. Hoeveel tulpen houdt hij over?

Deze som is al een stuk complexer dan de som met de bananen. Je kind moet meer informatie verwerken en verschillende bewerkingen uitvoeren:

• De bloemist heeft 26 tulpen.

• De bloemist maakt 6 boeketten met 4 tulpen. Dat zijn in totaal 24 tulpen (6 x 4 tulpen).
• De vraag is hoeveel tulpen er overblijven na het maken van de 6 boeketten.
  26 tulpen – 24 tulpen = 2 tulpen
  

Stel dat je kind de tafels nog niet geautomatiseerd heeft en er ook geen tafelkaart voorhanden is. Dan moet je kind nog een extra bewerking doen: de keersom 6 x 4 uitrekenen. Ook deze berekening neemt ruimte in in het werkgeheugen. De kans bestaat dat het werkgeheugen ‘overbelast’ raakt. Je kind kan de som dan niet meer uitrekenen. Dat is een negatieve ervaring. Daardoor kan je kind onzeker worden, een volgende keer bang zijn om te falen en blokkeren.

Als je kind de tafels nog niet geautomatiseerd heeft, maar er wél een tafelkaart is, kan je kind de som waarschijnlijk wel uitrekenen. Het werkgeheugen hoeft dan niet extra te worden belast, omdat het antwoord van de keersom 6 x 4 op de tafelkaart staat.

Is het gebruik van een tafelkaart wel goed?

Misschien vraag je je af of het gebruiken van een tafelkaart wel goed is. Leert en automatiseert je kind de tafels wel goed met een tafelkaart?

Je hoeft je hierover geen zorgen te maken. Een tafelkaart is een handig hulpmiddel. Bijvoorbeeld als je kind nog niet alle tafels goed heeft geautomatiseerd. Met de tafelkaart kan het dan toch de sommen maken waarin de keersommen slechts een onderdeel zijn van de som.

Een tafelkaart is ook handig als je kind twijfelt aan een uitkomst. Als je kind de som en de uitkomst vaak ziet, kan het de som ook automatiseren. Voor de makkelijke tafels zal je kind de tafelkaart waarschijnlijk niet snel gebruiken. Voor de moeilijkere tafels kan het gebruik een uitkomst zijn! Op een gegeven moment heeft je kind alle tafels geautomatiseerd en is de tafelkaart niet meer nodig.

Als je kind alle tafels voldoende heeft geautomatiseerd, kan het met grotere getallen gaan rekenen. Ook kan je kind dan complexere sommen oplossen.

Tafelkaart tot 20

Vermenigvuldigen stopt niet bij de tafel van 10. Als de kale sommen en verhaalsommen in groep 6, 7 en 8 complexer worden, kan een tafelkaart tot 20 handig zijn. Hoe meer tafels je kind kent, hoe makkelijker het complexe opgaven kan oplossen. Het werkgeheugen wordt dan niet meer belast met de ‘eenvoudige’ vermenigvuldigingen. In plaats daarvan kan het helemaal worden gebruikt voor het oplossen van de werkelijke som.

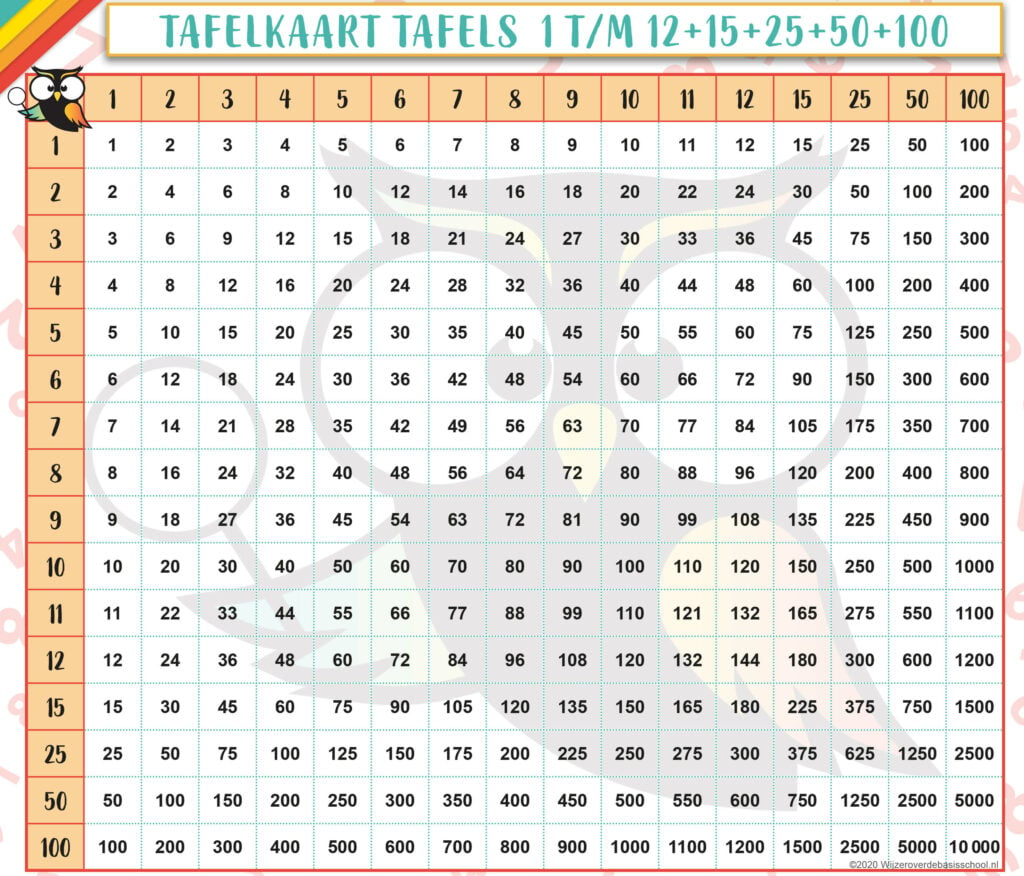
Tafelkaart tot 100

Als je kind te maken krijgt met breuken, kan de tafel van 25 van pas komen. Ook de tafels van 50 en 100 kunnen handig zijn. In de tafelkaart hieronder zijn alle belangrijke tafels gecombineerd.

Maak zelf een tafelkaart

Je kunt natuurlijk ook zelf een tafelkaart maken. Download hier een lege tafelkaart waarop je 10 tafels kunt invullen. Of download er eentje waarop ruimte is voor 20 tafels.

Veel plezier en succes!

Oefenbladen Rekenen Groep 4 (Gratis)

Download

Oefenbladen Rekenen Groep 5 (Gratis)

Download

Carola de Koning, BEd

Carola heeft ervaring opgedaan als bijlesjuf, kindercoach en als leerkracht in het basisonderwijs

Over Carola