Tafels oefenen groep 4 met flitskaarten en 7 spelletjes
In groep 4 begint je kind met het leren van de tafels. In dit artikel geef ik je een aantal tips waarmee je het tafels oefenen in groep 4 makkelijker en leuker kunt maken.
In groep 3 is je kind al bezig geweest met het zogenaamde herhaald optellen. Met materiaal worden steeds groepjes gemaakt. Groepjes blokjes, snoepjes, potloden enz. Geleidelijk aan leren kinderen dat ze niet 1 voor 1 alle items hoeven tellen, maar dat ze ook per groepje kunnen tellen.
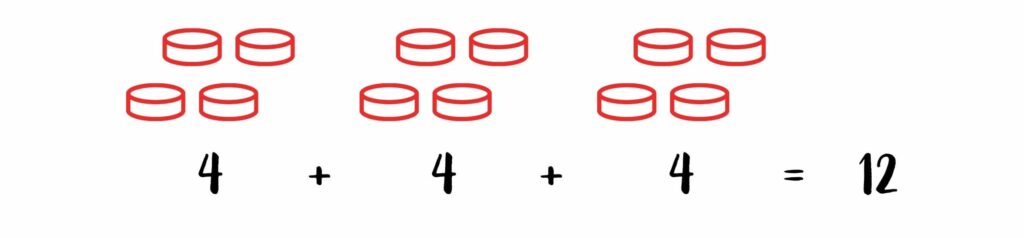
Oftewel: 3 groepjes van 4 is bij elkaar 12. Hier wordt eindeloos mee geoefend, ook op de getallenlijn:
Maar ook in rasters:
Je kind ziet hier óf 5 groepjes van 4 (verticaal) óf 4 groepjes van 5 (horizontaal). Het leert zo dat 5 groepjes van 4 evenveel is als 4 groepjes van 5. Later kan het dit inzicht gebruiken bij het omdraaien van de keersommen (5 x 3 = 3 x 5) In groep 4 leert je kind om de term ‘groepjes van’ te vervangen door het x-teken. 5 groepjes van 4 verandert in het abstractere 5 x 4. Het is belangrijk dat het verband tussen het herhaald optellen en de bijbehorende keersom goed wordt aangeleerd en verankerd.
Tafels oefenen groep 4: wat doe je als het moeilijk gaat?
Maar al te vaak zie ik in mijn praktijk kinderen bij wie dit mis is gegaan. Ze hebben wel de tafels uit hun hoofd geleerd, maar hebben geen beeld bij de keersommen. Ze kunnen er geen verhaal bij bedenken, en soms lukt het ze ook niet om het neer te leggen met materiaal. Je zult begrijpen dat het dan ook lastig wordt om een keersom te halen uit een verhaalsom.
Je kunt je kind helpen door thuis steeds keersommen te koppelen aan concrete situaties:
- Hoeveel stoelpoten staan er onder de tafel? Welke som je kunt gebruiken om dat snel uit te rekenen?
- Snijd boterhammen in 6 stukjes en vraag hoeveel stukjes het in totaal zijn. Welke som is dat?
- Hoeveel tanden zitten er in totaal aan alle vorken die op tafel liggen?
- Hoeveel tegels liggen er op het terras? (…rijen van … tegels).
Vraag steeds welke som erbij hoort. Gebruik daarbij de termen ‘keer’ en ‘groepjes van’. Dus bij de stoelen: 4 groepjes van 4 is 4 x 4 = 16. Laat je kind ook zelf zulke sommen bedenken. Misschien is het leuk om er een speciaal schriftje voor aan te leggen, waarin je kind ook verhaaltjes bij de keersommen kan tekenen en de sommen erbij kan schrijven.
Of ga met deze leuke box met spellen aan de slag om op een effectieve manier spelenderwijs te oefenen:
Rekenbox – Tafels van Vermenigvuldiging
Oorspronkelijke prijs was: 72,89.59,00Huidige prijs is: 59,00.
Let hier goed op bij het oefenen van de tafels in groep 4
Haalt jouw kind het keerteken en het plusteken door elkaar? Dit kan te maken hebben met het rijpingsproces van de hersenen. Bij andere kinderen gaat de koppeling mis tussen de mondelinge som en de schrijfwijze ervan. Je kunt je kind in beide gevallen helpen door dit tekeningetje thuis op te hangen en/of op school op te plakken op het tafeltje.
Snapt je kind eenmaal wat een keersom is, dan zal het meestal ook geen moeite hebben om via herhaald optellen tot een antwoord te komen. Maar dat herhaald optellen moet vervangen gaan worden door andere manieren om de som sneller uit te rekenen. Sommige kinderen kunnen de uitkomsten van de keersommen snel onthouden. Deze sommen hebben zij dan gememoriseerd.
Memoriseren en automatiseren
Memoriseren is iets anders dan automatiseren. Als je kind een som geautomatiseerd heeft, betekent dat dat het een manier heeft gevonden om de som snel, binnen 10 seconden, uit te rekenen. Memoriseren betekent dat je kind de som gewoon weet. Je kan het bij wijze van spreken midden in de nacht wakker maken en vragen hoeveel 3 x 6 is, en het antwoord komt meteen. Er is in de hersenen een directe koppeling gemaakt tussen de som en het antwoord.
Sommige kinderen slaan de stap van het automatiseren over. Zij onthouden heel snel het antwoord bij de som. Dit zijn vaak kinderen die ook makkelijk liedjes uit hun hoofd leren. Ze onthouden gewoon makkelijk opeenvolgende klanken. Of ze hebben een goed visueel geheugen, en onthouden dus sommen makkelijk als ze ze een paar keer gezien hebben. Dit zijn vaak kinderen die het altijd opmerken als iemand een andere bril heeft of die erg goed zijn in Memory. Deze kinderen gebruiken hun sterke visuele kant om de tafels gelijk te memoriseren.
Overigens betekent het goed kunnen memoriseren van keersommen nog niet dat deze kennis toegepast kan worden in verhaalsommen! Daarvoor is het belangrijk om steeds de koppeling keer is hetzelfde als ‘groepjes van’ te leggen.
Wat als memoriseren niet zo makkelijk gaat?
Maar niet bij alle kinderen gaat dat memoriseren zo vlot. Om toch van het herhaald optellen tot een snellere manier van uitrekenen te komen (automatiseren), wordt geoefend met verschillende strategieën:
Verdubbelen: 3 x 3 = 9 dus 6 x 3 is het dubbele, dus 18.
Begrijpt jouw kind dit niet, laat het dan zien met materiaal (evt. met een spiegeltje) en leg nog een keer de koppeling met ‘groepjes van’.
6 groepjes van 3 is het dubbele van 3 groepjes van 3.
Eentje meer/minder: 6 x 5 = 30 dus 5 x 5 is één groepje minder dus 30-5.
Tafels groep 4 oefenen met stoplichtkaartjes
Op een meer gestructureerde manier kun je oefenen met de zogenaamde stoplichtkaartjes. Dat gaat zo:
Maak groene, gele en rode kaartjes zoals hierboven (je kunt ook witte kaartjes gebruiken en de sommen in kleur). Je bepaalt de tafel waarmee je kind gaat oefenen, bijvoorbeeld 4. Dan wijs je eerste de makkelijke, groene kaartjes aan: 1 x 4, 10 x 4, 5 x 4, en laat je kind de antwoorden zeggen. Weet je kind de 5x niet? Herinner het dan aan de omgekeerde som, 4 x 5 of aan het feit dat 5 x de helft is van 10 x.
Gaan de groene kaartjes goed? Ga dan steeds van groen naar geel. Dus van 1 x 4 naar 2 x 4, van 5 x 4 naar 6 x 4 en weer 5 x 4 en dan 4 x 4 en tot slot van 10 x 4 naar 9 x 4. Gaan ook de gele kaartjes vlot, dan kun je van geel naar rood gaan. Op deze manier leert je kind om makkelijke tafelsommen te gebruiken om de moeilijkere uit te rekenen. Het mooiste is natuurlijk als je kind niet meer hoeft te rekenen, maar het ‘gewoon’ weet. Dat is helaas niet alle kinderen gegeven.
Je kunt ook oefenen met de flitskaartjes. Deze zijn gratis te downloaden:
Flitskaarten Tafels groep 4/5 (Gratis)
Tafels groep 4 oefenen met doosjes
Nog een andere manier van oefenen:
Je hebt 3 doosjes/bekers nodig, 1 met een gele sticker, 1 met een rode en 1 met een groene sticker. Schrijf de tafelsommen op kleine kaartjes, en zet het antwoord op de achterkant. Leg de somkaartjes naast elkaar neer. Je kind pakt nu steeds een kaartje en geeft het antwoord. De sommen die goed zijn, gaan in het gele doosje, degene die fout zijn gaan in het rode doosje.
De sommen uit het rode doosje worden herhaald: de sommen die dan goed zijn verhuizen naar het gele doosje, degene die weer fout zijn blijven in het rode doosje. De sommen uit het gele doosje worden herhaald: de goede gaan naar groen, de foute weer naar rood. Dan weer verder met rood enz. Net zo lang tot alles in het groene doosje zit. Iedere dag even herhalen doet wonderen! Het is leuk als je steeds de tijd opneemt die je kind nodig heeft om alle kaartjes in het groene doosje te krijgen.
Het motiveert je kind extra als het ziet dat dat iedere dag een beetje sneller gaat. Als het uiteindelijk binnen een minuut lukt, is het tijd voor een feestje!
7 Tafelspelletjes voor groep 4
Sommige kinderen kunnen de tafelsommen wel memoriseren, maar durven er niet op te vertrouwen. Zij blijven de sommen voor de zekerheid toch nog uitrekenen. Deze kinderen hebben een zetje nodig. Je kunt de volgende spelletjes met ze doen:
1. Bewegend leren
Uit steeds meer onderzoeken blijkt dat leren, en zeker memoriseren, makkelijker gaat als je erbij beweegt. Als je beweegt, gebruik je beide hersenhelften. Je linkerhersenhelft stuurt namelijk de rechterkant aan qua beweging en andersom.
2. Kaatsenballen
Je gooit een bal tegen de muur terwijl je een keersom vraagt. Jouw kind vangt de bal en gooit hem gelijk terug tegen de muur terwijl hij het antwoord zegt. Het is belangrijk om in een soort ritme te komen. Weet je kind het antwoord niet gelijk, zeg het antwoord dan voor en herhaal de som nog 2 keer.
3. Bal overrollen
Ga tegenover elkaar zitten, op de grond of aan tafel. Terwijl je de bal naar je kind toe rolt, zeg je een tafelsom. Je kind moet de bal gelijk terugrollen terwijl het het antwoord zegt. Als je kind het antwoord niet binnen 2 seconden weet, zeg jij het antwoord en rolt de bal weer terug waarbij je dezelfde som vraagt. Herhaal dit nog een keer en ga door naar de volgende som. Vraag de moeilijke sommen vaker dan de makkelijke, maar vraag ook de makkelijke om frustratie te voorkomen.
4. Touwtje springen/trampoline springen
Laat je kind springen. Als het eenmaal in een ritme zit, vraag je een keersom. Het antwoord moet in de volgende sprong komen, anders zeg je het weer voor en herhaal je de som nog 2 keer voordat je verder gaat.
Op bovenstaande spelletjes zijn veel variaties te bedenken, maar het belangrijkste is dat er een ritme is waarbinnen de antwoorden moeten komen, zodat je het idee krijgt van het ouderwetse tafels dreunen van vroeger.
5. Tafels oefenen op muziek
Is jouw kind gek op zingen? Zoek dan online naar liedjes waar de tafels gezongen worden. Het meezingen kan dan ook nog gecombineerd worden met lekker swingen, waarmee je de samenwerking van de hersenhelften weer stimuleert. Nog leuker is het natuurlijk als je kind zelf een melodie kan bedenken bij de tafelsommen! Bij iedere tafel gebruik je een andere melodie.
6. Voor de visuele denker
Voor de kinderen die goed zijn in het onthouden van wat ze zien, is het goed als ze zo vaak mogelijk de tafelsommen met het goede antwoord zien. Je kunt een blad met een bepaalde tafel bijvoorbeeld op het toilet of boven de eettafel hangen. Print iedere tafel in een andere kleur, kleur helpt de hersenen namelijk met onthouden. Ook een leuk idee: plak briefjes met de tafelsommen op de trap, op iedere traptrede een andere tafelsom. Eerst op volgorde, een paar dagen later door elkaar.
7. Ezelsbruggetjes
Plak een tafelsom die je kind niet kan onthouden op iedere deur, in grote gekleurde cijfers. Of verzin er een tekeningetje bij. Ik had ooit een leerling die zich steeds vergiste in de som 7 x 7. Omdat 5 x 5 25 is en 6 x 6 36 dacht hij steeds dat 7 x 7 47 was. Hij heeft uiteindelijk een tekening gemaakt van een surfer op zee die een hele hoge golf op zich af zag komen. In het tekstballonnetje: NEE!..genenveertig. Iedere keer als ik hem op school tegenkwam, hoefde ik alleen 7 x 7 te zeggen terwijl ik een golfbeweging met mijn hand maakte, en dan riep hij al: negenenveertig!
Nog een ezelsbruggetje bij een lastige som: 8 x 7. Als je die som met zijn uitkomst opzegt, hoor je de getallen in aflopende volgorde: 8 keer 7 is 6 en 5tig.
Met enige creativiteit zijn er bij meer lastige sommen wel zulke ezelsbruggetjes te verzinnen. Zelfverzonnen ezelsbruggetjes werken overigens het beste!
Bekijk ook:
- Rekenen groep 4
- Tafels leren groep 4
- Flitskaarten tafels groep 4 (gratis)
- Tafels oefenen uitleg en de beste oefentips
- Tafels oefenen groep 5
- Tafelkaarten
- Wat leren kinderen in groep 4?
- Redactiesommen groep 4
- Cito-toetsen groep 4
- Werkbladen groep 4
Oefenbladen Rekenen Groep 4 (Gratis)
Oefenbladen Begrijpend lezen Groep 4 (Gratis)
Oefenbladen Spelling Groep 4 (Gratis)
Oefenbladen Klokkijken Groep 4/5 (Gratis)
Mirjam Schumacher, BEd Master SEN
Mirjam behaalde een Bachelor of Education (PABO) en een Master SEN. Ze werkte als leerkracht en journaliste en heeft een eigen praktijk voor Remedial Teaching
Gerelateerde artikelen
Tafels oefenen groep 5 met spelletjes (+ handig ezelsbruggetje)
Tafels oefenen: uitleg en de beste oefentips
Tafels leren groep 4: zo help jij je kind
Reacties
2 reacties op “Tafels oefenen groep 4 met flitskaarten en 7 spelletjes”-
Ik wil graag een tafel plaat
-
Beste Coen,
In dit artikel kun je allerlei tafelkaarten downloaden:https://wijzeroverdebasisschool.nl/uitleg/tafelkaarten
Heb je hier iets aan?
Hartelijke groet,
Carola
-
Natalie –
Handig materiaal dat de kinderen aanspreekt om speels te leren.