Breuken groep 6: uitleg met video

Lees alles over breuken in groep 6 in dit artikel en help jouw kinderen met breuken oefenen. Breuken vormen een belangrijk onderdeel van rekenen in groep 6. Een breuk is eigenlijk een gebroken getal dat tussen 2 hele getallen in zit.

Je leert:

• wat tellers, noemers en breukstrepen zijn;
• hoe je breuken kunt verdelen;
• hoe je ze kleurt;
• hoe je ze uitspreekt;
• en hoe je ze op een getallenlijn zet.

Ook kun je de informatie uit dit artikel terugzien in een video. Ten slotte krijg je de kans lekker veel sommen met breuken te oefenen!

Rekenen groep 6: breuken

Het allereerste wat je moet begrijpen als je met breuken wilt gaan rekenen, is wat een breuk precies is. Het woord ‘breuk’, komt van het woord ‘breken’. Je hebt het over iets wat niet meer heel is, maar gebroken.

Denk maar eens aan je arm. Als je die breekt, heb je een breuk. Je arm is dus ‘gebroken’.

Bij het rekenen met breuken gaat het ook over breken. Je breekt spullen of vormen in stukken. Of je breekt getallen in stukken.

Belangrijk om te weten: bij rekenen met breuken gaat het altijd over breken in gelijke, even grote stukken. Het gaat altijd over eerlijk verdelen.

Dat is bij een gebroken arm natuurlijk wel anders! Die breekt niet in precies twee even grote, gelijke stukken. Bij rekenen doen we dat wel.

Download de (gratis) Werkbladen Breuken groep 6/7/8

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Breuken aanleren groep 6

Om je te laten zien hoe rekenen met breuken werkt, laten we je wat voorbeelden zien.

We beginnen met een lekkere eierkoek.

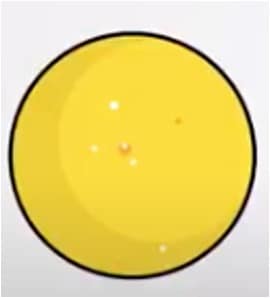
Marieke wil hem in de pauze delen met haar klasgenootje. Om dat goed te doen, verdeelt ze de eierkoek eerlijk in 2 gelijke stukken.

Nu ziet de eierkoek er zo uit:

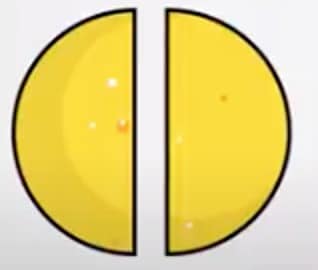
Nu Marieke de eierkoek in 2 gelijke stukken heeft verdeeld, kan ze 1 deel zelf opeten en het andere deel aan haar klasgenootje geven.

Het stuk dat Marieke opeet, is een breuk: het is de helft van de gebroken eierkoek. Het andere stuk voor haar klasgenoot is ook een breuk, namelijk de andere helft.

Hetzelfde kun je doen met deze chocoladereep.

Kaya wil deze reep delen met 3 andere kinderen. In totaal zijn ze dus met z’n vieren. Kaya wil hem zo breken dat alle kinderen evenveel chocola hebben.

Eerst deelt ze de reep in twee even grote stukken.

Daarna deelt ze allebei de stukken ook weer door de helft. Dat ziet er zo uit:

Kaya heeft nu 4 gelijke stukken chocola. Dat betekent dat zij en de andere kinderen allemaal evenveel chocola kunnen snoepen!

Kaya heeft de reep nu verdeeld onder 4 mensen. Ze heeft van deze reep dus 4 breuken gemaakt. Iedereen krijgt 1 van de 4 stukjes.

Hoor je dat je bij het maken van deze breuken ook heel vaak het woord ‘delen’ gebruikt?

Eerst zeiden we: Marieke gaat de eierkoek delen met haar klasgenoot. Daarna ging Kaya de chocoladereep verdelen in 4 stukken. Ze heeft de reep gedeeld voor 4 kinderen.

En dat is niet zo raar. Want rekenen met breuken heeft alles te maken met goed kunnen delen! Maar dan wel met eerlijk delen. Iedereen krijgt evenveel of even grote stukken!

Breuken met vormen

In onze vorige voorbeelden braken we steeds ‘echte dingen’ in stukjes. We maakten zo van een eierkoek en een chocoladerep breuken. Maar wist je dat je ook vormen in stukken breken? Kijk maar mee.

Deze cirkel lijkt een beetje op de eierkoek van net. Ze hebben dezelfde vorm:

Het getal ‘1’ in de cirkel geeft aan dat dit 1 hele cirkel is.

Deze cirkel kun je ook verdelen stukjes. Eerst maak je er twee stukken van. Kijk, we delen hem doormidden.

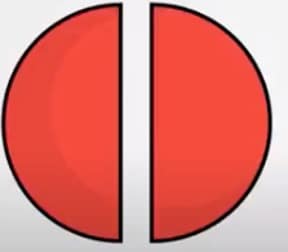
De linkerkant en de rechterkant zijn nu allebei een breuk geworden: beide zijn ze 1 deel van de hele cirkel. Ofwel: 2 aparte delen van het geheel.

Samen zijn ze weer de hele cirkel.

Omdat de linkerkant nu de helft is, 1 van de 2 stukken, noem je dit ½ deel. En de rechterkant is ook 1 van de 2 stukken, dus ook dit deel heet ½ deel.

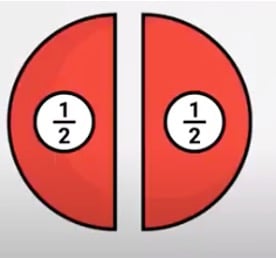
Nu hebben we breuken uit de rekenles in beeld. Dit zijn nou breuken!

Je kunt natuurlijk ook meer stukjes maken dan 2.

Kijk maar eens naar deze rechthoek:

Die gaan we in 4 stukken delen.

Nu heb je 4 breuken gemaakt, die samen weer een hele zijn. Ieder stukje is een breuk.

Omdat de rechthoek nu in 4 stukken is verdeeld, noem je 1 stukje nu 1 van de 4 stukken. In breukentaal heet dat ¼ deel. Het stukje ernaast is ook 1 van de 4 stukken, dus ook dat heet ¼ deel.

Hetzelfde geldt voor de andere twee stukken, die heten ook allemaal ¼ deel. En samen zijn ze weer een hele.

Je kunt de rechthoek ook verdelen in 8 stukken. Kijk maar:

Je hebt nu 8 stukken die samen een hele zijn. Hoe zou 1 stukje nu heten?

Juist!

Het is 1 stukje van de 8, dus 1/8 deel!

En zo kun je vormen blijven verdelen in allerlei stukjes. Om te weten hoe 1 stukje heet, bekijk je steeds in hoeveel stukjes de cirkel of de rechthoek is verdeeld:

• 1 van de 3 stukjes = 1/3 deel
• 1 van de 5 = 1/5 deel
• En 1 van de 16 stukjes = 1/16 deel

Breuken inkleuren

We hebben je nu laten zien hoe je spullen of vormen verdeelt in stukjes, waarbij iedereen 1 stukje krijgt.

Maar soms… heb je gewoon zin in meer. Jij hebt toch ook wel eens zin in 2 of 3 stukjes pizza, in plaats van maar in 1? Nou…dat kan geregeld worden hoor! We laten je met een pizza zien hoe dat werkt.

Hier zie je een pizza. Deze pizza is al in stukjes gesneden.

Laten we eerst even tellen in hoeveel stukken de pizza is gesneden. De pizza is verdeeld in 8 stukken. Deze ene punt is 1 van de 8 punten en heet dus in breukentaal 1/8 deel.

Maar aan 1 zo’n stukje pizza hebben we natuurlijk niet genoeg. Jij lust vast wel drie van deze stukken!

We hebben nu 3 van de 8 stukken gepakt. In breukentaal heb je nu 3/8 deel van deze pizza op je bord liggen.

Hetzelfde kun je ook weer doen met vormen.

Als voorbeeld nemen we een rechthoek. Dit is de opdracht:
Kleur van deze rechthoek 4/12 deel. Hoe pak je dat nou aan?

Kijk eerst naar de breuk. Wat betekent deze breuk? 4/12 deel betekent 4 van de 12 stukjes. Je moet deze rechthoek dus eerst in 12 stukjes verdelen. Wel eerlijk delen, hè? Alle stukjes moeten even groot zijn.

Zo, gedaan. Nu kleur je 4 van de 12 stukjes in, zodat je weet dat het om die stukjes gaat.

Nu heb je een breuk gekleurd. Namelijk 4/12 deel van een rechthoek.

We doen nog een voorbeeld.

Kleur de cirkel voor 2/3 deel in.

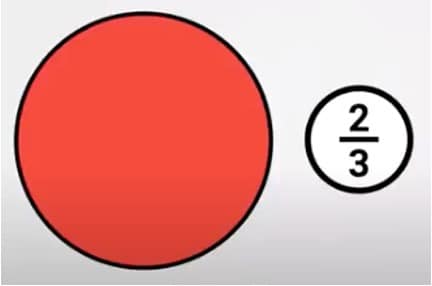
Lees eerst de breuk nog eens rustig in je hoofd voor. 2/3 deel… Dat betekent 2 van de 3 stukjes.

Nu weet je dat je eerst de cirkel in drie stukjes moet verdelen. Dan ziet hij er zo uit:

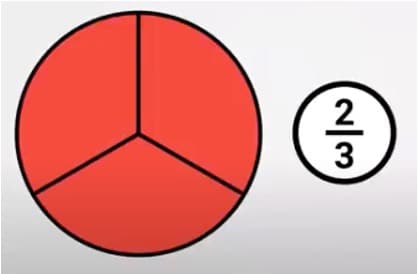
Vervolgens moet je 2 van de 3 stukjes kleuren. Dan krijg je dit:

Nu heb je 2/3 deel van de cirkel ingekleurd!

Hoe is een breuk opgebouwd?

Je hebt nu al geleerd wat een breuk is, hoe je spullen en vormen in breuken verdeelt en hoe je breuken kunt inkleuren. Dan is het nu tijd je te laten zien hoe een breuk is opgebouwd.

Je hebt al gezien hoe je een breuk moet schrijven. Maar wat staat er nou eigenlijk? 1/8 betekent 1 van de 8 stukjes.

Boven de streep staat de 1. Het getal boven de streep noemen we de teller.

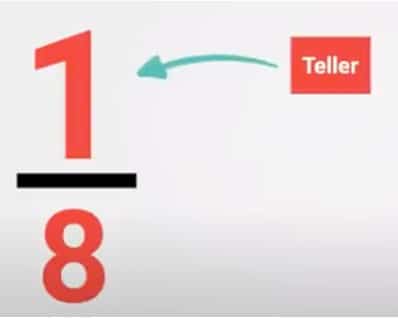
Het woord ‘teller’ komt van ‘tellen’. Je telt daar om hoeveel stukjes het gaat. De teller is in deze breuk 1, omdat het nu maar om 1 stukje gaat.

Onder de streep staat de 8. Dat betekent 8 stukjes. Onder de streep staat altijd in hoeveel stukjes iets verdeeld is. Dit is de noemer. Het woord ‘noemer’ komt van noemen. Omdat dit 8 stukjes zijn, noemen we deze breuk ‘achtsten’. De noemer is 8.

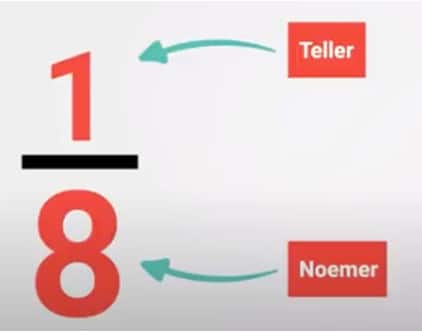
In het midden van de breuk staat de streep. Dit is de breukstreep. Als je deze streep ziet, weet je dat je te maken hebt met een breuk. Daarom gebruiken we de naam breukstreep.

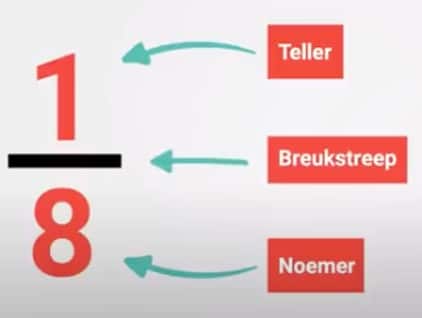
Deze streep wordt ook wel de deelstreep genoemd, omdat breuken zoveel met delen en verdelen te maken hebben. Je bent altijd vormen of spullen in stukjes aan het delen, vandaar de naam deelstreep.

Hoe spreek je een breuk uit?

We hebben het nu uitgebreid over breuken gehad. Maar hoe spreek je een breuk eigenlijk uit?

Voor een breuk zijn een heleboel verschillende uitspraken:

• Je kunt zeggen: ‘twee derde’ of ‘drie zevende’. Deze uitspraak komt heel vaak voor.
• Ook goed is: ‘twee van de drie’ of ‘drie van de zeven’.
• Of je zegt: ‘twee op de drie kinderen is misselijk geworden’.
• Of, zoals we dit artikel begonnen: ‘1 eierkoek gedeeld door 2’.

Dit zijn allemaal verschillende, goede uitspraken voor breuken.

Breuken getallenlijn groep 6

Maar hoe zit het nu als je een breuk op de getallenlijn wilt zetten? Waar moet die dan staan?

Weet je het nog? Een getallenlijn is een lijn met getallen erop, die in de juiste volgorde staan. 0, 1, 2, 3, 4 enzovoort.

We weten intussen dat breuken delen zijn van hele getallen. Laten we eens makkelijk beginnen: een halve pizza is groter dan 0 pizza’s en kleiner dan 1 pizza.

Omdat het precies om de helft van de pizza gaat, 1 van de 2 stukken dus, moet de breuk 1/2 ook precies tussen de 0 en de 1 liggen op de getallenlijn.

Je deelt de getallenlijn tussen de 0 en de 1 in 2 gelijke delen. Precies in het midden daarvan komt een streepje, met daarbij de breuk 1/2.

Let op: je hoeft hier niet 2 streepjes te zetten, omdat de noemer 2 is. Dan zou je namelijk de ruimte tussen de 0 en de 1 in 3 stukken verdelen, in plaats van 2.

Als je het getal 1/5 op de getallenlijn wilt zetten, doe je hetzelfde. Eerst kijk je naar de noemer. Die zegt dat je in dit geval de ruimte tussen 0 en 1 in 5 gelijke delen moet verdelen. Dat zijn dus 4 streepjes.

De teller is 1, dus je weet nu dat de breuk 1/5 op het 1e streepje tussen de 0 en de 1 moet komen.

Stel nu dat je de breuk 4/5 op de getallenlijn moet zetten. Je kunt daarvoor dezelfde getallenlijn gebruiken. Ook hier moet het vlak tussen 0 en 1 namelijk in 5 gelijke delen verdeeld worden.

Maar nu is de teller 4. Dat betekent dat de breuk bij het 4e lijntje vanaf de 0 moet komen staan. Kijk, zo:

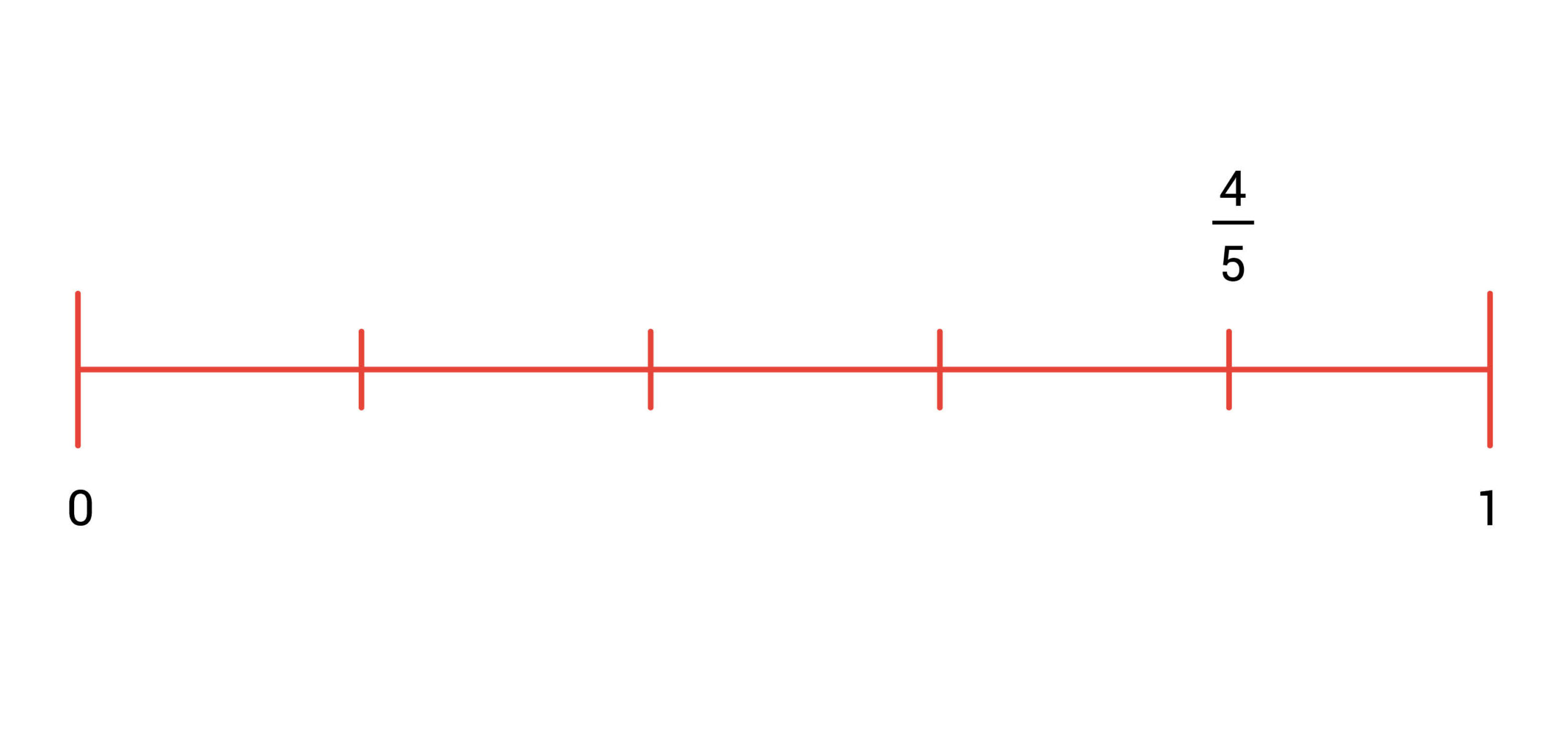
Als je de breuken 1/2 en 1/5 op dezelfde getallenlijn zou zetten, zie je heel snel welke breuk het grootste is, namelijk 1/2. Die staat namelijk dichter bij de 1 dan 1/5.

Zet je daar ook nog 4/5 bij, dan zie je dat die nog groter is dan 1/2.

Een getallenlijn gebruiken is dus een superhandige manier om te zien welke breuk het grootst of het kleinst is.

Redactiesommen breuken groep 6

Redactiesommen zijn sommen die in een verhaaltje verstopt zitten. Zo’n verhaaltjessom kan best lastig zijn, omdat je niet meteen ziet welke som je moet uitrekenen.

In dit artikel over redactiesommen vind je een heel praktisch stappenplan voor het rekenen met verhaaltjessommen.

Voor redactiesommen waar breuken in verstopt zitten kun je precies hetzelfde stappenplan gebruiken.

Daarnaast is het belangrijk dat je de som uittekent. Als je bijvoorbeeld een rechthoek of een cirkel met het juiste aantal delen tekent, kun je daarna de breuken inkleuren.

In het artikel over redactiesommen staat ook uitgelegd hoe je een cirkel op de juiste manier in 3 gelijke delen kunt verdelen. Ook worden er voorbeelden gegeven van redactiesommen met breuken. Superhandig!

Les breuken groep 6 op video

Vind jij het fijner om alle plaatjes in beeld te hebben bij de uitleg? Bekijk dan eens onderstaande video over breuken. Die zal je vast helpen de informatie goed op te slaan.

Word jij de nieuwe breukkampioen?

Nu jij deze informatie hebt gelezen over breuken, weet jij supergoed wat breuken zijn en hoe ze in elkaar zitten. Dat betekent dat je klaar bent om met breuken te gaan rekenen. Je kunt er namelijk van alles mee doen:

• breuken gelijknamig maken
• breuken vereenvoudigen
• breuken optellen
• breuken aftrekken
• breuken vermenigvuldigen
• breuken delen

En met de oefenopgaven hieronder word jij zeker de nieuwe breukkampioen! Je oefent alles waarover je hierboven hebt gelezen. Daarnaast kun je ook breuken oefenen aan de hand van een breukenposter. Veel succes met oefenen. Als je vragen hebt, stel ze dan hieronder in een reactie.

Breuken oefenen groep 6

Hier vind je opdrachten waarmee je de theorie oefent. De antwoorden staan onderaan de pagina.

Opdracht 1

Schrijf van de volgende breuken de teller en de noemer op.

1. 1/3

Teller =
Noemer =

2. 4/5

Teller =
Noemer =

3. 9/29

Teller =
Noemer =

4. 4/13

Teller =
Noemer =

5. 23/25

Teller =
Noemer =

Opdracht 2

Kleur van de volgende vormen de juiste delen.

1/6

3/4

6/8

2/3

7/8

Antwoorden opdracht 1

1. 1/3

Teller = 1
Noemer = 3

2. 4/5

Teller = 4
Noemer = 5

3. 9/29

Teller = 9
Noemer = 29

4. 4/13

Teller = 4
Noemer = 13

5. 23/25

Teller = 23
Noemer = 25

Antwoorden opdracht 2

1/6

3/4

6/8

2/3

7/8

Werkblad breuken groep 6

Hier vind je nog een aantal opdrachten waarmee je de theorie oefent. Ook van deze sommen staan de antwoorden onderaan de pagina.

Opdracht 1

Zet de volgende breuken op de juiste plek op de getallenlijn.

1. 1/2
2. 2/3
3. 4/6
4. 2/5
5. 4/10

Opdracht 2

Kleur van de volgende vormen de juiste delen.

1. 3/8
2. 9/12
3. 2/24
4. 5/8
5. 4/6

Antwoorden opdracht 1

Zet de volgende breuken op de juiste plek op de getallenlijn.

Simone, kun jij ervoor zorgen dat de breuken echt goed op de getallenlijn komen? Voor mij is het in dit Wordbestand moeilijk om ze precies goed te krijgen. Ik heb er alle vertrouwen in dat jij daar meer tools voor hebt.

1. 1/2
2. 2/3
3. 4/6
4. 2/5
5. 4/10

Antwoorden opdracht 2

1/2

2/3

4/6

2/5

4/10

Rochelle Schaepkens, BEd Master EN

Rochelle behaalde een Bachelor en Master of Education (PABO en Master Leren en Innoveren). Daarnaast heeft ze de opleidingen tot Taalexpert, Rekenexpert en Remedial Teaching gevolgd. Ze heeft 20 jaar ervaring als leerkracht en unitleider op een basisschool. Nu werkt ze als docent op de Pabo en als Content Creator voor Wijzer over de basisschool.

Over Rochelle