Breuken aftrekken: de beste uitleg over minsommen met breuken

Breuken aftrekken ofwel minsommen met breuken echt goed begrijpen? Hier vind je alle uitleg en kun je meteen oefenen.

Minsommen met breuken, wanneer kom je die nou tegen? Nou, daar hoef je niet eens lang voor te zoeken. Stel, je viert je verjaardag. Aan het eind van de dag heb je van de taart nog 5/8 deel over. Je weet dat er nog 3 mensen op bezoek komen. Heb je dan nog genoeg taart?

Om het antwoord op die vraag te weten, moet je breuken van elkaar kunnen aftrekken. Hoe je dát doet, leggen we je uit in dit artikel.

We gaan je vertellen:

• hoe je gelijknamige breuken van elkaar aftrekt.
• hoe je gemengde gelijknamige breuken van elkaar aftrekt.
• hoe je breuken van elkaar aftrekt, waarbij je een heel getal moet inwisselen voor een breuk.

Bekijk ook:

• Breuken oefenen: de complete handleiding
• Zo gebruik je een breukenposter
• Breuken optellen
• Breuken vermenigvuldigen
• Breuken delen
• Breuken gelijknamig maken
• Breuken vereenvoudigen
• Kleinste gemene veelvoud
• Procenten berekenen
• Breuken groep 6
• Deel van het geheel berekenen

Download hier de (gratis) Werkbladen Breuken Groep 6/7/8

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Uitleg breuken aftrekken

Zoals je al wel weet, bestaat een breuk uit een teller en een noemer. De teller staat boven de breukstreep en de noemer eronder.

We spreken van gelijknamige breuken als de noemers van 2 breuken hetzelfde zijn. De tellers mogen wel verschillend zijn.

Zo zijn 1/6 en 4/6 gelijknamige breuken, maar 1/6 en 4/7 niet.

De hoofdregel voor minsommen met gelijknamige breuken is simpel: als je gelijknamige breuken van elkaar gaat aftrekken, haal je altijd alleen de tellers van elkaar af. De tellers zijn dus eigenlijk de minsom.

De noemers blijven gelijk. Daar hoef je dus niets mee te doen.

We geven je een voorbeeld:

3/4 – 2/4 =

Als je deze som wilt uitrekenen, haal je de tellers van elkaar af. Dat is een simpel sommetje: 3 – 2 = 1.

De noemers laat je staan. De uitkomst krijgt dus ook dezelfde noemer: 4.

Je weet nu dat de uitkomst van deze som 1/4 moet zijn.
Waarom je alleen de tellers van elkaar aftrekt en de noemers niet, laten we je nu zien.

We gaan daarvoor nog eens terug naar de vorige voorbeeldsom:

3/4 – 2/4 =

Om duidelijk te maken hoe deze rekensom precies werkt, halen we er wat pannenkoeken bij.

Om te beginnen kleuren we 3/4 van de pannenkoek. Dat ziet er zo uit:

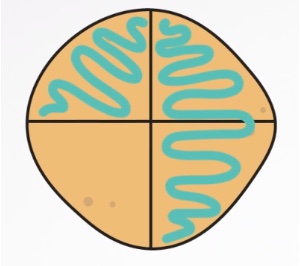
Dat ene deeltje dat over is, mag je wegdenken. Iemand heeft het al opgegeten.

Van die 3/4 pannenkoek eet je 2/4 deel op. Je haalt dus van 3/4 in feite 2/4 deel af. Om te laten zien hoeveel je dan nog overhoudt, zetten we door die 2/4 een kruis.

Kijk, zo:

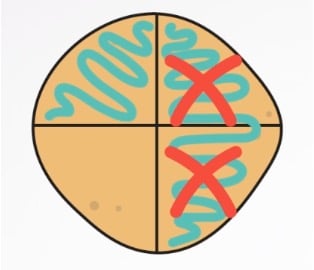
Als je eerst 3/4 pannenkoek had en je at daar nog 2/4 deel van op, blijft er dus 1/4 deel over. Zie je dat de noemers nog steeds hetzelfde zijn? Alleen de tellers heb je van elkaar afgetrokken.

Als je toch de noemers van elkaar had afgehaald, dan was je op een heel raar, fout antwoord uitgekomen.

Kijk maar:

3/4 – 2/4 zou dan 1/0 zijn. Nou, dat lijkt natuurlijk helemaal nergens op! Zo werkt het dus NIET.

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

Breuken min elkaar

We gaan nog eens wat sommen oefenen.

12/15 – 5/15 =

We beginnen met teller – teller. Dan krijg je de som 12 – 5 =. Het antwoord is natuurlijk 7. Die 7 schrijf je alvast op bij de uitkomst, op de plaats van de teller.

De noemer blijft gelijk, dus 15. Dat betekent dat je die 15 ook in de uitkomst op de plaats van de noemer neer mag zetten.

De uitkomst van deze som is dus 7/15.

12/15 – 5/15 = 7/15

We doen nog een som.

7/8 – 4/8 =

Deze breuken zijn ook gelijknamig, dus we kunnen op dezelfde manier te werk gaan.

Teller – teller is 7 – 4. Dat is 3. De 3 komt op de plaats van de teller.

De noemer blijft gelijk: 8.

De uitkomst van deze som is dus 3/8.

7/8 – 4/8 = 3/8.

Niet zo moeilijk, toch?

We doe er nog eentje:

9/12 – 3/12 =

We kijken eerst weer naar de teller: 9 – 3 = 6
De noemer blijft gelijk, namelijk 12.

De uitkomst is dus 6/12.

Maar… let goed op! Dit antwoord mag je zo niet laten staan! Bij breuken is de afspraak dat je de breuk ALTIJD vereenvoudigt als dat kan. Je maakt de getallen in de breuk zo klein mogelijk.

Laten we eens kijken hoe we deze breuk kunnen vereenvoudigen.

Door welk getal kun je de teller en de noemer delen? Je kunt zowel de teller als de noemer delen door 2.

Teller: 6 : 2 = 3
Noemer: 12 : 2 = 6

Dan krijg je dus 3/6 als uitkomst.

Kun je deze breuk nog verder vereenvoudigen? Jazeker! Je kunt beide getallen door 3 delen!

Teller: 3 : 3 = 1
Noemer: 6 : 3 = 2

De uitkomst, 1/2, kun je niet nóg verder vereenvoudigen. Dat betekent:

9/12 – 3/12 = 1/2

Overigens hebben wij de breuk nu met tussenstappen vereenvoudigd. Als jij dat in 1 keer kan, is dat natuurlijk ook prima! Doe wat voor jou handig is.

Uit dit voorbeeld blijkt wel dat het met breuken aftrekken opletten geblazen is. Als je denkt dat je je antwoord hebt, moet je dus altijd checken of je de breuk nog kunt vereenvoudigen!

Breuken aftrekken met helen: gemengde breuken

Soms heb je ook te maken met gemengde breuken in een rekensom. Dat betekent dat minimaal 1 van de getallen niet alleen uit een breuk bestaat, maar ook een heel getal in zich heeft. Hoe je dan te werk gaat, laten we je nu zien.

We gebruiken daarvoor een voorbeeldsom:

2 3/4 – 1/4 =

Je ziet dat het getal 2 3/4 een gemengde breuk is. Vooraan staat namelijk een heel getal (2), dat wordt gevolgd door een breuk (3/4).

Het getal dat je er vanaf gaat trekken, is 1/4. Dat is geen gemengde breuk.

We maken er voor het gemak even een plaatje bij. De samengestelde breuk 2 3/4 ziet er zo uit:

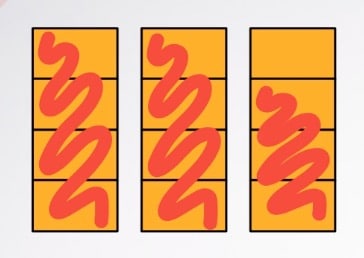
Je ziet 2 volledig gekleurde rechthoeken. Die staan samen voor de 2 in de som. Van de derde rechthoek is nog 3/4 deel gekleurd.

Hiervan moet je 1/4 deel afhalen. Dat is dus 1 zo’n klein vakje. We zetten er even een kruis doorheen:

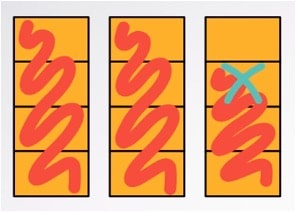
De vraag is wat er nu overblijft.

Met de hele rechthoeken is niks gebeurd. Dus er blijven sowieso 2 helen over. Die kun je alvast in je antwoord noteren.

Daarnaast blijft er nog 2/4 deel over. Die schrijf je achter de 2 helen. Het antwoord is dus 2 2/4.

Ho, stop! Kun je dit getal nog kleiner maken? Ja, dat kan! Je kunt de teller en de noemer beide nog delen door 2. De helen hoef je niet kleiner te maken.

Dus de helen, de 2, schrijf je alvast op.

En dan deel je bij 2/4 de teller en de noemer nog door 2. De uitkomst daarvan is 1/2.

De uitkomst van de som is dan dus 2 1/2.

2 3/4 – 1/4 = 2 1/2

We doen nog een voorbeeld:

5 5/6 – 3 4/6 =

Kijk, nu heb je te maken met twee gemengde breuken. In dat geval trek je eerst de hele getallen van elkaar af.

5 – 3 = 2

De 2 helen schrijf je vast op in je antwoord. Daarna ga je door met de breuken.

5/6 – 4/6 = 1/6

Kun je die nog kleiner maken? Nee, dat kan niet.

De uitkomst van de som is dus 2 1/6.

5 5/6 – 3 4/6 = 2 1/6

Van 1 hele een breuk maken

We maken het nog een stapje moeilijker met dit voorbeeld:

6 1/8 – 5/8 =

Eens kijken, we zien een gemengde breuk en een gewone breuk.

Je ziet misschien ook al wel een andere lastigheid: je moet dadelijk 5/8 van 1/8 afhalen. Hoe moet je dat dan doen? Want als je 1 – 5 doet, krijg je een getal onder de 0.

Het is het handigst om deze som even te tekenen. Dan zie je beter wat er gebeurt.

We tekenen 6 gekleurde rechthoeken. Van rechthoek nummer 7 is nog 1/8 deel gekleurd.

Hier staat eigenlijk hetzelfde als 6 1/8.

Nu moet je hier 5/8 deel vanaf halen.

1/8 deel is sowieso geen probleem. Daar kun je alvast een kruis doorheen zetten.

Nu moet je er nog 4/8 deel vanaf halen. En dat is natuurlijk lastiger. Maar gelukkig heb je een tekening gemaakt. Daardoor kun je 1 hele rechthoek heel gemakkelijk verdelen in 8 stukjes: 8/8!

Dan ziet de tekening er zo uit:

Van die 8/8 kun je nu zonder problemen 4/8 deel af halen. Zet daarvoor door 4 van die kleine delen een kruisje:

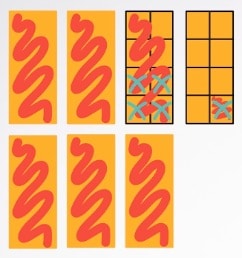
Nu zie je in 1 oogopslag wat je overhoudt als je van 6 1/8 5/8 aftrekt! Je hoeft alleen nog maar de helen en de delen te tellen.

We tellen 5 helen. Daarnaast tellen we nog 4 kleine deeltjes. Die deeltjes staan allemaal voor 1/8. Je hebt dus naast die 5 helen nog 4/8 deel over.

Het antwoord is dus 5 4/8. Dit getal moet je nog wel even vereenvoudigen. Zowel de 4 als de 8 kun je door 4 delen. De teller komt dan uit op 1 en de noemer op 2.

De definitieve uitkomst van de som is dan dus 5 1/2.

6 1/8 – 5/8 = 5 1/2

En zie je wat we hebben gedaan om de som makkelijker te maken? Van 1 van de helen hebben we een breuk gemaakt. Op die manier lukte het ineens wél de som uit te rekenen.

Een aftreksom met 2 gemengde breuken

Zo’n zelfde som doen we nog een keer, maar dan met 2 gemengde breuken.

4 2/5 – 2 3/5 =

Dat is een pittige som! We moeten nu én met helen, én met breuken werken! Daarom is het slim ook nu de som te tekenen. In dit geval gebruiken we cirkels.

We beginnen met 5 cirkels. 4 daarvan kleuren we helemaal. Dat zijn de 4 helen. Van de 5e cirkel kleur je slechts 2 van de 5 delen: 2/5 deel. Samen vormen deze gekleurde cirkels 4 2/5 deel.

Van 4 2/5 moeten we nog 2 3/5 deel af halen. Die 2 helen zijn natuurlijk niet zo moeilijk. Je zet daarvoor gewoon een kruis door 2 volledig gekleurde cirkels. Dat ziet er dan zo uit:

Je ziet dat je nu nog 2 2/5 deel over hebt. Daar moet je nog 3/5 vanaf halen. Je ziet al dat het moeilijk is om dat te doen. Daarom verdeel je vast 1 van de overgebleven gekleurde cirkels in 5 delen. Kijk, zo:

Nu heb je van 2 2/5 eigenlijk 1 7/5 gemaakt. En van 1 7/5 haal je wél heel gemakkelijk 3/5 af:

Je ziet nu ook meteen wat je overhoudt aan het einde van deze som: 1 4/5 deel.

1 4/5 kun je niet vereenvoudigen. We kennen nu dus de uitkomst van deze moeilijke som.

4 2/5 – 2 3/5 = 1 4/5

Stap voor stap gelijknamige breuken aftrekken

Zoals je ziet, is het niet altijd eenvoudig om gelijknamige breuken snel van elkaar af te trekken. Gelukkig weet je intussen dat je gebruik kunt maken van tekeningen om de som wat makkelijker te maken.

Samengevat heb je dit geleerd in dit artikel:

• Je kan gelijknamige breuken van elkaar aftrekken.
• Je kan gemengde, gelijknamige breuken van elkaar aftrekken.
• Je kan breuken van elkaar aftrekken, waarbij je een heel getal moet inwisselen voor een breuk.

Natuurlijk leer je pas écht goed hoe je gelijknamige breuken van elkaar aftrekt, als je er mee oefent. Daarom staan hieronder nog wat oefenbladen, waar je lekker zelf mee aan de slag kunt.

Vind jij gelijknamige breuken aftrekken moeilijk of juist makkelijk? Laat het ons weten in een reactie.

Breuken aftrekken oefenen

Op dit oefenblad vind je minsommen met breuken. Maak de opdrachten waar nodig met een kladblaadje, zodat je de moeilijke sommen kunt uittekenen. De antwoorden vind je onder de opdrachten.

Opdracht 1

Bereken deze minsommen met gelijknamige breuken.

1. 7/8 – 3/8 =
2. 6/9 – 4/9 =
3. 2/3 – 2/3 =
4. 14/15 – 12/15 =
5. 7/12 – 3/12 =

Opdracht 2

Bereken deze minsommen met gemengde, gelijknamige breuken.

1. 2 3/8 – 2/8 =
2. 14 8/9 – 5/9 =
3. 25 4/6 – 3/6 =
4. 12 1/4 – 3/4 =
5. 23 2/8 – 7/8 =

Opdracht 3

Bereken deze minsommen met gemengde, gelijknamige breuken.

1. 3 7/9 – 1 5/9 =
2. 6 6/8 – 4 2/8 =
3. 4 2/5 – 2 3/5 =
4. 13 4/9 – 8 8/9 =
5. 7 1/5 – 6 4/5 =

Antwoorden

Antwoorden opdracht 1

1. 7/8 – 3/8 = 4/8 = 1/2
2. 6/9 – 4/9 = 2/9
3. 2/3 – 2/3 = 0
4. 14/15 – 12/15 = 2/15
5. 7/12 – 3/12 = 4/12 = 1/3

Antwoorden opdracht 2

1. 2 3/8 – 2/8 = 2 1/8
2. 14 8/9 – 5/9 = 14 3/9 = 14 1/3
3. 25 4/6 – 3/6 = 25 1/6
4. 12 1/4 – 3/4 = 11 2/4 = 11 1/2
5. 23 2/8 – 7/8 = 22 3/8

Antwoorden opdracht 3

1. 3 7/9 – 1 5/9 = 2 2/9
2. 6 6/8 – 4 2/8 = 2 2/8 = 2 1/4
3. 4 2/5 – 2 3/5 = 1 4/5
4. 13 4/9 – 8 8/9 = 4 5/9
5. 7 1/5 – 6 4/5 = 2/5

Breuken minsommen werkblad

Op dit oefenblad vind je ook minsommen met breuken. Gebruik eventueel weer een kladblaadje. De antwoorden vind je onder de opdrachten.

Opdracht 1

Bereken deze minsommen met gelijknamige breuken.

1. 6/14 – 4/14 =
2. 13/25 – 8/25 =
3. 65/110 – 54/110 =
4. 9/432 – 9/432 =
5. 32/40 – 24/40 =

Opdracht 2

Bereken deze minsommen met gemengde, gelijknamige breuken.

1. 23 7/8 – 4/8 =
2. 74 9/11 – 9/11 =
3. 13 2/15 – 8/15 =
4. 43 1/4 – 3/4 =
5. 834 8/20 – 18/20 =

Opdracht 3

Bereken deze minsommen met gemengde, gelijknamige breuken.

1. 12 12/13 – 8 10/13 =
2. 39 7/18 – 2 1/18 =
3. 72 3/9 – 7 6/9 =
4. 345 2/15 – 1 7/15 =
5. 1492 6/20 – 362 16/20 =

Antwoorden

Antwoorden opdracht 1

1. 6/14 – 4/14 = 8/14 = 4/7
2. 13/25 – 8/25 = 5/25 = 1/5
3. 65/110 – 54/110 = 11/110 = 1/10
4. 9/432 – 9/432 = 0
5. 32/40 – 24/40 = 8/40 = 1/5

Antwoorden opdracht 2

1. 23 7/8 – 4/8 = 23 3/8
2. 74 9/11 – 9/11 = 74
3. 13 2/15 – 8/15 = 12 9/15
4. 43 1/4 – 3/4 = 42 2/4 = 42 1/2
5. 834 8/20 – 18/20 = 833 10/20 = 833 1/2

Antwoorden opdracht 3

1. 12 12/13 – 8 10/13 = 4 2/13
2. 39 7/18 – 2 1/18 = 37 6/18 = 37 1/3
3. 72 3/9 – 7 6/9 = 64 6/9 = 64 2/3
4. 345 2/15 – 1 7/15 = 343 10/15 = 343 2/3
5. 1492 6/20 – 362 16/20 = 1129 10/20 = 1129 1/2

Rochelle Schaepkens, BEd Master EN

Rochelle behaalde een Bachelor en Master of Education (PABO en Master Leren en Innoveren). Daarnaast heeft ze de opleidingen tot Taalexpert, Rekenexpert en Remedial Teaching gevolgd. Ze heeft 20 jaar ervaring als leerkracht en unitleider op een basisschool. Nu werkt ze als docent op de Pabo en als Content Creator voor Wijzer over de basisschool.

Over Rochelle