
Weet jij al wat breuken zijn? Dan kun je een stapje verder gaan. In dit artikel leren we je alles over ‘het deel van het geheel berekenen‘. Dat is een hoeveelheid.
Als je dit artikel gelezen hebt, weet je:
- hoe je een deel van het geheel kunt uitrekenen;
- hoe je het geheel kunt berekenen als je een deel (de breuk) kent.
Bekijk ook:
- breuken gelijknamig maken
- breuken vereenvoudigen
- breuken optellen
- breuken aftrekken
- breuken vermenigvuldigen
Breuk als deel van het geheel
“Je kunt een deel van een geheel uitrekenen…”
Die zin klinkt misschien een beetje gek. Wat bedoelen we daar precies mee? Dat leggen we je nu uit.
Als je een deel uitrekent, betekent dat dat je ‘een stukje’ wilt gaan uitrekenen. Een breuk is maar een stukje van het geheel; het is niet alles. Met ‘geheel’ bedoelen we ‘alles’, de hele.
Bijvoorbeeld: 1 pannenkoek is het geheel. Een halve pannenkoek is daar een deel van. Een half kun je ook als breuk schrijven: 1/2. Die breuk is slechts een deel van de pannenkoek, namelijk de helft. De helft van de pannenkoek is 1 van de 2 delen.

Je kunt hetzelfde doen met gehelen die groter zijn dan 1. Zo kun je bijvoorbeeld ½ deel van 12 uitrekenen.
- ½ is dan het deel, het stukje, de breuk.
- En 12 is het geheel. 12 is alles, 12 is de hele.
Om deze som makkelijker te maken, tekenen we een reep met 12 stukjes. De reep is de hele, het geheel.

Van die reep kleuren we ½ deel. ½ deel is de breuk. 1/2 deel betekent 1 van de 2 delen. Je moet dus eerst de reep in 2 gelijke groepen verdelen. Daarna kleur je 1 van die 2 groepen:

Je kunt nu uitrekenen wat ½ deel van 12 is. Dat doe je door de gekleurde vakjes te tellen. Dan zie je dat 1/2 deel van 12 stukjes hetzelfde is als 6 stukjes. 1/2 deel van 12 is dus 6.
Download hier de (gratis) Werkbladen Breuken Groep 6/7/8

Oefenbladen Rekenen Groep 8 (Gratis)
Oefenen met deel van het geheel
Dit gaan we wat vaker oefenen, met een aantal verschillende opdrachten. Zo weet je straks zelf goed hoe je een deel van het geheel berekent.
De opdracht is steeds hetzelfde: reken het deel van het geheel uit.
De eerste som luidt als volgt:
¼ deel van 12 auto’s = … auto’s
In deze som is ¼ deel de breuk. Het geheel is 12. 12 auto’s. Hoeveel is ¼ deel van 12?
Teken eerst weer het geheel; 12 auto’s dus.

Nu wil je weten hoeveel 1/4 deel van deze auto’s is. De noemer van de breuk is 4. Dat betekent dat je deze 12 auto’s in 4 groepjes moet verdelen.

Je ziet nu 4 groepjes. 1 groepje is ¼ deel. Nu hoef je alleen nog maar te tellen hoeveel auto’s er in 1 groepje zitten. Dat zijn 3 auto’s.
¼ deel is dus hetzelfde als 3 auto’s.
We doen nog een som.
Een chocoladereep heeft 24 blokjes.
Farah eet 1/3 deel op.
Hoeveel blokjes eet Farah op?
En hoeveel blokjes zijn er nog over?
Als je sommen hebt waarbij je een deel van het geheel moet uitrekenen, is het altijd handig om de som te tekenen. Doordat je tekent, kun je namelijk zien wat je aan het doen bent.
Teken eerst een reep van 24 blokjes. Want 24 blokjes is in deze som het geheel.

Farah eet van deze reep 1/3 deel op. Dat betekent dat je 1/3 deel moet kleuren. Omdat de noemer 3 is, weet je dat je de reep nu in drie stukken moet verdelen.
24 : 3 = 8
In 1/3 deel zitten dus 8 stukjes.

We gaan even terug naar de vraag. Wat moesten we ook alweer weten?
De eerste vraag was: hoeveel blokjes eet Farah op?
Dat antwoord weet je al. Farah eet 1/3 deel op. In de tekening zie je dat dat 8 stukjes zijn.
Maar er stond nog een vraag: hoeveel blokjes zijn er nog over?
Dat kun je nu ook heel gemakkelijk zien.
Er waren 24 blokjes, Farah heeft er 8 opgegeten… 24 – 8 = 16
Er zijn dus nog 16 blokjes over! Dit kun je controleren in de tekening. Ook daar zie je dat 16 blokjes niet gekleurd zijn.
Sommen met breuken zonder verhaaltjes
De vorige voorbeelden waren sommen die verpakt zaten in een verhaaltje.
Je krijgt ook vaak opdrachten zonder verhaaltje erbij. Zoals deze:
- 2/5 deel van 45 is …
- 4/5 deel van 55 is …
Kijk maar eens mee hoe je dit soort sommen uitrekent.
We beginnen bij de eerste som: 2/5 deel van 45 is …
Ook nu is tekenen erg handig, dus teken iets wat je gemakkelijk in even grote stukken verdeelt. Een reep bijvoorbeeld.
De reep van deze som is 45 waard. Je hoeft de reep niet te verdelen in 45 stukjes, maar je moet wel goed onthouden dat het geheel 45 is.

We moeten weten hoeveel 2/5 deel van het geheel is. Van 45 dus. De noemer van de breuk is 5. Dat betekent dat je de reep in 5 stukjes moet verdelen.

Nu moet je bedenken hoeveel 1 zo’n deel waard is. Daarvoor deel je 45 (het geheel) door 5.
45 : 5 = 9

Je weet nu dat 1/5 deel 9 waard is. Dan weet je ook 2/5 deel.
2/5 deel is 2 x 9, dus 18. 2/5 deel van 45 is 18.

We gaan bij de volgende som eens kijken of het ons ook lukt de som uit te rekenen zonder te tekenen. Probeer hem in plaats daarvan maar eens voor je te zien in je hoofd.
Dit is de som:
4/5 deel van 55 is …
Om deze som uit te rekenen, moet je eerst weten wat 1/5 deel is.
Want als je dat weet, dan weet je straks ook hoeveel 4/5 deel is. Je ziet dat de noemer 5 is. Beeld je maar eens een rechthoek in die je in 5 stukken moet verdelen. 1 stukje is dan 1/5 deel. De rechthoek is in zijn geheel 55 waard. Je deelt de rechthoek, 55 dus, door 5.

55 : 5 = 11
Met andere woorden: 1/5 deel van 55 staat gelijk aan 11.
Nu moeten we even goed opletten. We moesten namelijk niet 1/5 deel weten, maar 4/5 deel.
Om van 1/5 deel 4/5 deel te maken, moet je 1/5 x 4 doen. Hetzelfde doe je nu met 11.
11 x 4 = 44
We weten nu dat 4/5 deel van 55 hetzelfde is als 44. 4/5 deel van 55 is 44!
Nog 3 oefensommen
We doen nog eens 3 oefensommen die we stap voor stap gaan uitrekenen. Als oefening kun je de sommen eerst zelf maken, voordat je verder leest. Wanneer je klaar bent of er zelf niet uit komt, bekijk je onze uitwerkingen en antwoorden.
Dit zijn de sommen:
- 3/5 deel van 15 is …
- 6/7 deel van 560 is…
- 8/9 deel van 1800 is…
Ga je gang, reken ze maar uit! Ben je klaar met rekenen? Bekijk dan nu onze uitwerkingen.
Uitwerking som 1
De eerste som was 3/5 van 15.
Eerst gaan we weer 1/5 deel uitrekenen. Het geheel is 15. Die deel je door 5, want de noemer van de breuk is 5.
15 : 5 = 3
1/5 deel is dus 3. Nu moet je nog uitrekenen hoeveel 3/5 deel is. Daarvoor doe je 3 x die 3. Dat is 9.
3/5 deel van 15 is 9.
Uitwerking som 2
Som 2 was: 6/7 van 560.
Eerst reken we 1/7 deel uit. Daarvoor verdeel je 560 in 7 stukken.
560 : 7 = 80
Dat is niet zo’n makkelijke som. Om het jezelf makkelijker te maken, kun je met een tussenstap werken. Je kent vast de uitkomst van 56 : 7 wel. Dat is 8. 560 is 10 x 56. Dat betekent dat de uitkomst van 560 : 7 ook 10 x zo groot moet zijn. 80 dus!
1/7 deel is dus 80. Voor de som moeten we weten hoeveel 6/7 deel van 560 is. Dat is dan 6 x 80.
6 x 80 = 480
6/7 deel van 560 is dus 480.
Uitwerking som 3
Voor som 3 moet je uitrekenen hoeveel 8/9 deel van 1800 is.
Eerst rekenen we weer 1/9 deel uit. Je deelt 1800 door 9. De uitkomst daarvan is 200.
Nu moet je nog uitrekenen hoeveel 8/9 deel dan is. Daarvoor doe je 200 x 8. Uit die som komt 1600.
8/9 deel van 1800 is 1600.
Andersom rekenen: reken het geheel uit
Je hebt nu geleerd hoe je een deel van een geheel uitrekent. Maar wist je dat je dit soort sommen ook wel eens andersom tegenkomt?
We leggen je daarom nu uit hoe je het geheel uitrekent als je maar een deel weet.
Kijk bijvoorbeeld eens naar deze opdracht:
1/9 deel van een boek is 40 bladzijdes. Hoeveel bladzijden heeft dan het gehele boek?
Je weet nu maar 1 deel. Namelijk dat 1/9 deel van het boek 40 bladzijden heeft. Hoeveel bladzijden heeft het hele boek dan?
Hieronder zie je dat we het boek hebben getekend en dat we het in 9 stukken hebben verdeeld. Dat hebben we gedaan, omdat de noemer 9 is. 1 deel van het boek is 40 bladzijdes.

We willen weten hoeveel bladzijdes het hele boek heeft. Het hele boek is 9/9 deel.
Om het antwoord op die vraag te vinden, moeten we 9 x 40 bladzijdes doen.
9 x 40 is 360

Het hele boek heeft dus 360 bladzijdes.
Nu hebben we het geheel uitgerekend, terwijl we maar een deel wisten.
We doen er nog eentje:
5/8 deel is 2,50 euro. Hoeveel is het geheel?
Om deze som makkelijker te maken, tekenen we een cirkel. We willen straks weten hoeveel de hele cirkel waard is. Dat weten we nu nog niet. We weten wél dat 5/8 deel 2,50 euro waard is.
Daarom verdelen we de cirkel in 8 stukken. De noemer is immers 8. We kleuren 5 van de 8 delen in. Daarvan weten we dat het in totaal 2,50 waard is. De cirkel ziet er nu zo uit:
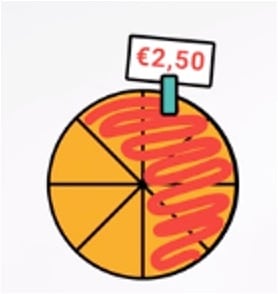
Nu is het handig om te weten hoeveel 1/8 deel waard is. We verdelen de 2,50 euro over de 5 stukken. 1 stukje is 50 cent waard.
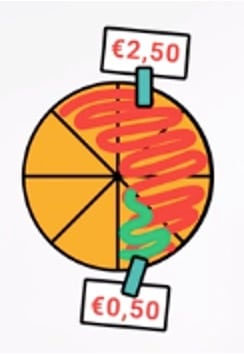
Nu kunnen we de hele cirkel berekenen.
De hele cirkel is 8 x 50 cent.
8 x 50 is 400 Het geheel is dus 400 cent waard, ofwel 4 euro.
We doen nog een voorbeeld:
2/5 deel is 60 liter. Hoeveel liter is dan 5/5 deel?
Laten we eens kijken of we deze som kunnen uitrekenen zonder te tekenen. In plaats daarvan rekenen we nu de som in ons hoofd uit. We proberen het voor ons te zien.
Denk aan een rechthoek. Die rechthoek is in 5 stukken verdeeld. 2 van de 5 stukken zijn samen 60 liter.

Om nu te weten hoeveel 1 van die 5 stukken waard is, moet je de 60 delen door 2.
60 : 2 = 30 liter.
1/5 deel is dus 30 liter. En 2/5 deel is 60 liter, dat wisten we al.
Maar hoeveel is dan 5/5 deel? Als 1/5 deel 30 liter is, dan is 5/5 deel 5 keer zoveel.
5 x 30 = 150 liter
We doen nog 1 laatste som, een som in een verhaaltje. Eens kijken of je die nu ook kunt oplossen.
- Op het feestje van Gea zijn 16 gasten aanwezig. Dit is 4/5 deel van alle uitgenodigde gasten. Hoeveel gasten heeft Gea uitgenodigd?
Laten we eens goed naar de som kijken. Daarin zien we dat 4/5 deel van het geheel 16 is.
Maar wat is de vraag ook weer?
De vraag is: hoeveel gasten zijn uitgenodigd?
We moeten dus uitrekenen hoeveel gasten in totaal zijn uitgenodigd. Alle gasten bij elkaar staat gelijk aan 5/5 deel.
Als we weten dat 4 van de 5 stukken samen 16 waard zijn, kunnen we ook berekenen hoeveel 1 stuk waard is. We moeten dan 16 delen door 4.
16 : 4 = 4
1/5 deel is dus hetzelfde als 4 gasten.
Om nu 5/5 deel te weten, doe je 5 x 4 gasten. Dat is 20.
In totaal heeft Gea 20 mensen uitgenodigd.
Van geheel naar deel en van deel naar geheel
Nu je dit artikel gelezen hebt, weet je precies hoe het zit met delen en gehelen.
Je weet:
- hoe je een deel van het geheel kunt uitrekenen;
- hoe je het geheel berekent als je een deel (de breuk) kent.
Natuurlijk willen we heel graag dat de stof die je nu geleerd hebt, goed in je hersenpan wordt opgeslagen. Hoe meer je oefent, hoe beter je de theorie onthoudt! Daarom vind je hieronder een werkblad.
Heb jij nog vragen over het deel van een geheel? Vertel ons in een reactie wat je nog moeilijk vindt en wij proberen je zo goed mogelijk te helpen.
Breuken werkblad deel van een geheel
Op dit werkblad vind je een aantal opdrachten over het deel van een geheel. Teken de tussenstappen voor jezelf uit, zodat je ziet wat je doet. De antwoorden van de opdrachten vind je onderaan de pagina.
Opdracht 1
Reken het deel van het geheel uit.
- 1/3 van 15 snoepjes =
- 1/5 van 25 knikkers =
- 1/8 van 64 postzegels =
- 1/20 van 1400 mensen =
- 1/100 van 2000 rijstkorrels =
Opdracht 2
Reken het deel van het geheel uit.
- 2/5 van 15 erwtjes =
- 4/9 van 27 pennen =
- 3/10 van 110 stenen =
- 9/12 van 96 spaghettislierten =
- 15/100 van 800 boomblaadjes =
Opdracht 3
Reken uit hoeveel het geheel is.
- 1/6 deel is 8. Hoeveel is het geheel?
- 5/8 deel is 15. Hoeveel is het geheel?
- 3/10 deel is 18. Hoeveel is het geheel?
- Kim heeft 21 knikkers. Dat is 7/8 deel van het geheel. Hoeveel is het geheel?
- Dirk betaalt 64 euro voor nieuwe schoenen. Dat is 8/9 deel van zijn spaarpot. Hoeveel geld zat er in zijn spaarpot voordat Dirk de schoenen kocht?
Antwoorden opdracht 1
- 1/3 van 15 snoepjes = 5 snoepjes.
Je deelt het geheel, 15, door 3. Ieder deel is 5 snoepjes waard. - 1/5 van 25 knikkers = 5 knikkers.
Je deelt het geheel, 25, door 5. Ieder deel is 5 knikkers waard. - 1/8 van 64 postzegels = 8 postzegels.
Je deelt het geheel, 64, door 8. Ieder deel is 8 postzegels waard. - 1/20 van 1400 mensen = 70 mensen.
Je deelt het geheel, 1400, door 20. Ieder deel is 70 mensen waard. - 1/100 van 2000 rijstkorrels = 20 rijstkorrels.
Je deelt het geheel, 2000, door 100. Ieder deel is 20 rijstkorrels waard.
Antwoorden opdracht 2
- 2/5 van 15 erwtjes = 6 erwtjes
Je deelt het geheel, 15, eerst door 5, omdat de noemer van de breuk 5 is. 1/5 deel is 3 erwtjes waard. Voor 2/5 deel doe je dit getal x 2. De uitkomst daarvan is 6. - 4/9 van 27 kinderen = 12 pennen
Je deelt het geheel, 27, eerst door 9, omdat de noemer van de breuk 9 is. 1/9 deel is 3 pennen waard. Voor 4/9 deel doe je dit getal x 4. De uitkomst daarvan is 12. - 3/10 van 110 stenen = 33 stenen
Je deelt het geheel, 110, eerst door 10, omdat de noemer van de breuk 10 is. 1/10 deel is 11 stenen waard. Voor 3/10 deel doe je dit getal x 3. De uitkomst daarvan is 33. - 9/12 van 96 spaghettislierten = 72 spaghettislierten
Je deelt het geheel, 96, eerst door 12, omdat de noemer van de breuk 12 is. 1/12 deel is 8 spaghettislierten waard. Voor 9/12 deel doe je dit getal x 9. De uitkomst daarvan is 72. - 15/100 van 800 boomblaadjes = 120 boomblaadjes
Je deelt het geheel, 800, eerst door 100, omdat de noemer van de breuk 100 is. 1/100 deel is 8 boomblaadjes waard. Voor 15/100 deel doe je dit getal x 15. De uitkomst daarvan is 120.
Antwoorden opdracht 3
- 1/6 deel is 8. Het geheel is dan 48. Je weet dat 1/6 deel gelijk staat aan 8. Het geheel is 6/6 deel. Je moet dus 6 x 1/6 deel doen, dus 6 x 8. De uitkomst daarvan is 48.
- 5/8 deel is 15. Het geheel is dan 24. Eerst reken je 1/8 deel uit. Als je van 5/8 naar 1/8 wilt gaan, moet je delen door 5. Dat geldt dus ook voor het getal 15.
15 : 5 = 3
1/8 deel is 3. Het geheel is 8/8 deel. Je moet daarvoor 8 x 1/8 doen, dus 8 x 3. De uitkomst daarvan is 24. - 3/10 deel is 18. Het geheel is dan 60.
Eerst reken je 1/10 deel uit. Als je van 3/10 naar 1/10 wilt gaan, moet je delen door 3. Dat geldt dus ook voor het getal 18.
18 : 3 = 6
1/10 deel is 6. Het geheel is 10/10 deel. Je moet daarvoor 10 x 1/10 doen, dus 10 x 6. De uitkomst daarvan is 60. - Kim heeft 28 knikkers. Dat is 7/8 deel van het geheel. Het geheel is dan 32.
Eerst reken je 1/8 deel uit. Als je van 7/8 naar 1/8 wilt gaan, moet je delen door 7. Dat geldt dus ook voor het getal 28.
28 : 7 = 4
1/8 deel is 4.
Het geheel is 8/8 deel. Je moet daarvoor 8 x 1/8 doen, dus 8 x 4. De uitkomst daarvan is 32. - Dirk betaalt 64 euro voor nieuwe schoenen. Dat is 8/9 deel van zijn spaarpot. Hoeveel geld zat er in zijn spaarpot voordat Dirk de schoenen kocht?
Dirk had vóór de aankoop van zijn nieuwe schoenen 72 euro in zijn spaarpot.
Eerst reken je 1/9 deel uit. Als je van 8/9 naar 1/9 wilt gaan, moet je delen door 8. Dat geldt dus ook voor het getal 64.
64 : 8 = 8
1/9 deel is 8. Het geheel is 9/9 deel. Je moet daarvoor 9 x 1/9 doen, dus 9 x 8. De uitkomst daarvan is 72.

Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 6 (Gratis)





Dankje je hebt mijn dochter echt geholpen ze is nu veel slimmer gevorden, dankje!