
Nu jij alles weet over breuken, wordt het interessant om al die breuken op een getallenlijn te plaatsen. Hoe dat precies werkt, vertellen we je in dit artikel.
We geven je voorbeelden die passen bij het niveau van groep 6, groep 7 en groep 8.
Straks weet je precies:
- waar een breuk moet staan op de getallenlijn;
- welke breuk bij een aangewezen plaats moet staan;
- en hoe je breuken met verschillende noemers op de getallenlijn
plaatst.
Breuken getallenlijn uitleg
Je vraagt je misschien af waarvoor het handig is als je breuken op een getallenlijn kunt plaatsen. Wanneer je weet hoe dat werkt, kun je snel zien hoeveel een breuk waard is. Door verschillende breuken op een getallenlijn te plaatsen, kun je breuken op een handige manier met elkaar vergelijken.
Maar laten we bij het begin beginnen. Wat is een getallenlijn ook alweer? Je hebt hem vast al vaker voorbij zien komen in de rekenles. Als voorbeeld tekenen we een stukje van een getallenlijn, van 0 tot 5.
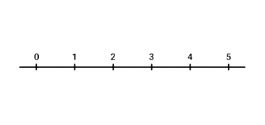
In dit artikel blijft het niet bij die simpele, hele getallen. We gaan nu ook breuken op de lijn plaatsen. Een breuk is niet een heel getal, maar een deel van een heel getal. Dat betekent dat de breuken op de getallenlijn tussen de hele getallen in staan.
Stel, je zoomt in op een getallenlijn tussen de 0 en de 2. Je ziet dan dat er nog allemaal kleine streepjes tussen die getallen staan:
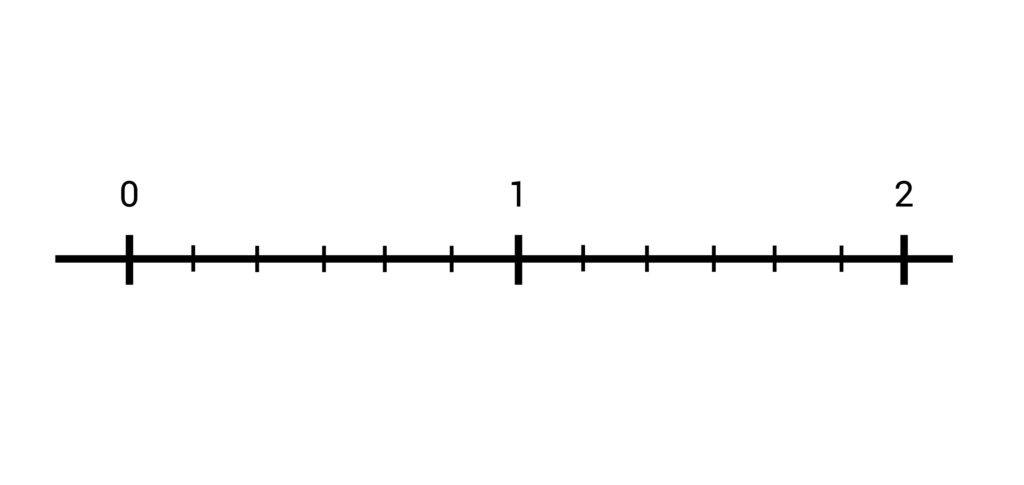
Tussen de hele getallen op de lijn liggen namelijk de gebroken getallen: de breuken.
Het getal 1/2 ligt bijvoorbeeld hier:
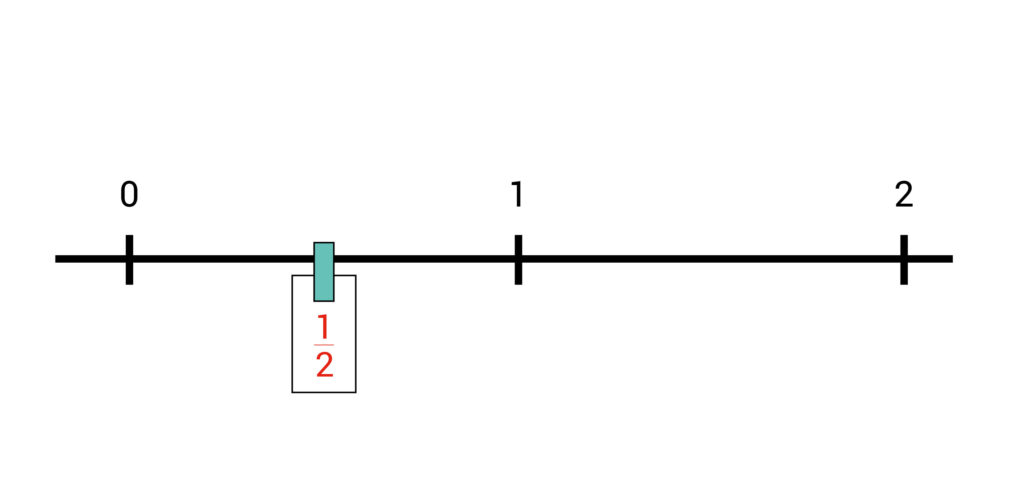
1/2 is namelijk de helft van 1. Deze breuk ligt dus precies tussen de 0 en de 1 in. Het getal 2 3/8 ligt ook tussen 2 getallen in: de 2 en de 3. 2 3/8 is groter dan 2 en kleiner dan 3.
Download de (gratis) Werkbladen Breuken Groep 6/7/8

Oefenbladen Rekenen Groep 8 (Gratis)
Breuken op de juiste plek
We gaan je nu laten zien hoe je de breuken op de juiste plek krijgt. Daarvoor gebruiken we een rechthoek en een getallenlijn. Die zetten we onder elkaar:
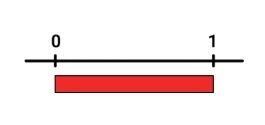
De strook en de getallenlijn lijken heel erg op elkaar. Kijk maar: de onderste lijn van de strook is eigenlijk hetzelfde als een getallenlijn.
Als je nu ¾ deel van de strook wilt kleuren, verdeel je de strook in 4 gelijke delen. Dat doe je, omdat de noemer 4 is. En de noemer geeft altijd aan in hoeveel stukken je iets moet verdelen. Nu kleur je 3 van de 4 stukken. Dan heb je dus 3/4 deel van de strook gekleurd:

Nu ga je naar de getallenlijn kijken. Die zet je erboven. Op de getallenlijn doe je precies hetzelfde als in de strook: je verdeelt de lijn in 4 stukken en je kleurt ¾ deel. Zet bij het streepje waar je uitkomt ¾ neer. Want tot daar is het ¾ deel. Zo ziet dat er dan uit:
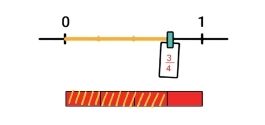
Als je een breuk moet kleuren of moet neerzetten op de getallenlijn, verdeel die dan altijd eerst in stukjes. Kijk naar de noemer om te zien hoeveel stukjes je nodig hebt. Daarna kleur of tel je het aantal stukjes dat je nodig hebt. Hoeveel dat er zijn, zie je aan de teller. Schrijf daarna de breuk op de lijn.
Breuken getallenlijn groep 6
In groep 6 maak je voor het eerst uitgebreid kennis met breuken. De getallenlijn ken je al. Vanaf dit jaar weet je ook hoe je breuken tussen de 0 en de 1 op zo’n getallenlijn moet plaatsen. Net zoals we hierboven deden dus!
We willen graag dat je deze stof goed begrijpt voordat we hem moeilijker maken. Daarom geven we je nog een voorbeeld. Dit keer gaan we de breuk 6/8 op de getallenlijn plaatsen.
Eerst maken we weer een getallenlijn, ingezoomd tussen de 0 en de 1. 6/8 is minder dan een hele, dus we hebben de getallenlijn maar nodig tot de 1.
Daarna verdelen we de lijn in stukjes. Weet je nog wat je daarvoor moet doen? Juist, je kijkt naar de noemer. De noemer is 8, dus ook de getallenlijn moet in 8 stukjes worden verdeeld. Om dat makkelijk te maken, verdeel je de lijn eerst in 2 helften. Daarna verdeel je die 2 stukken ook weer door midden. Dan heb je al 4 stukjes. Als je die 4 stukjes dan ook nog door de helft doet, ontstaan er 8 stukjes. De getallenlijn ziet er nu zo uit:
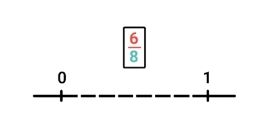
We moeten de breuk 6/8 op de lijn zetten. Om te weten waar 6/8 op de lijn moet liggen, kijk je naar de teller. Die is 6 waard. Dat betekent dat je 6 van de 8 stukjes moet kleuren. Aan het eind van dat gekleurde deel zet je de breuk 6/8 neer:
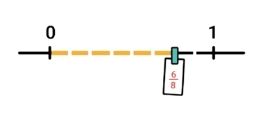
In groep 6 leer je ook hoe je andersom werkt. Je krijgt dan een getallenlijn te zien met pijltjes. Jij moet dan bedenken welke breuk bij de pijltjes ligt.
We geven je nu een voorbeeld van zo’n opdracht. Die opdracht ziet er zo uit:

Om te weten welke breuk bij het pijltje ligt, ga je eerst tellen in hoeveel stukjes de getallenlijn verdeeld is. Tel daarvoor de zwarte stukjes van de lijn; niet de witte streepjes!
Tussen de 0 en de 1 liggen 5 zwarte stukjes. Dat betekent dat de noemer van de breuk ook 5 moet zijn. Vervolgens bepaal je na welk stukje de pijl staat. Dat doe je door te tellen. In deze tekening staat hij na het 3e van de 5 stukjes. 3 van de 5 dus. Dan weet je ook dat de breuk 3/5 moet zijn! Schrijf bij de pijl 3/5 op.
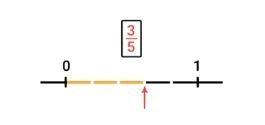
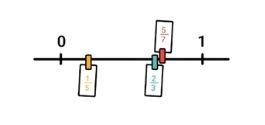
We doen er nog eentje voor. We zien weer een getallenlijn van 0 tot 1. Daarop staan twee pijlen getekend. Welke breuken horen bij de pijlen?
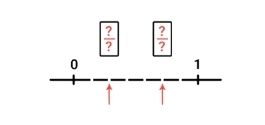
Tel eerst weer in hoeveel stukjes de lijn is verdeeld. We tellen 7 stukjes. De noemers van de breuken ken je nu: 7. Het eerste pijltje staat na het 2e stukje. Bij die pijl hoort dus de breuk 2/7. Het 2e pijltje staat achter het 5e stukje. Daar hoort dan de breuk 5/7 bij!
Breuken op de getallenlijn groep 7
Als je naar groep 7 gaat, worden de sommen met breuken op de getallenlijn een beetje moeilijker. Je weet nu al hoe je bepaalt welke breuk bij een pijltje ligt en waar een breuk op de getallenlijn moet staan. Maar tot nu toe waren die breuken steeds kleiner dan 1.
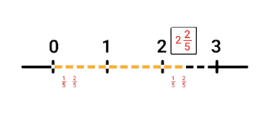
Er zijn natuurlijk ook breuken die groter zijn dan 1. Bijvoorbeeld de breuk 2 2/5. Hoe zet je die dan op de getallenlijn? Dat werkt eigenlijk precies hetzelfde. Alleen heb je nu een getallenlijn nodig die verder gaat dan 1. Kijk, deze getallenlijn gebruikten we net:
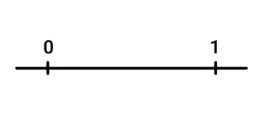
Maar het getal 2 2/5 past hier niet op. Je moet deze lijn langer maken. Voordat we dat gaan doen, kijken we goed naar het getal waar we mee te maken hebben. De breuk 2 2/5 betekent: 2 helen en nog 2/5 deel. Dat betekent dat je een lijn nodig hebt die langer is dan 2 helen. Teken daarom een getallenlijn tot de 3. Kijk, zo:
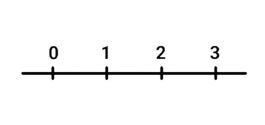
Om de breuk op de lijn te plaatsen, ga je de lijn weer in stukjes verdelen. Kijk naar de noemer, die is 5. De lijnen tussen de hele getallen verdeel je nu steeds in 5 stukken. Dan ziet de getallenlijn er zo uit:
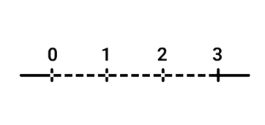
Nu gaan we bekijken waar 2 2/5 ligt. We kunnen natuurlijk gaan tellen vanaf het begin. 1/5, 2/5… Maar let op: Je moet niet 2/5 op de lijn zetten, maar 2 2/5! Dat betekent dat je direct een grote stap kunt zetten. 2 2/5 is namelijk groter dan 2 en kleiner dan 3.
Op de getallenlijn is vooral het stuk tussen de 2 en de 3 interessant. Je kunt er dus ook voor kiezen alleen de lijn tussen de 2 en de 3 in 5 stukjes te verdelen. Dat scheelt je een hoop werk! 2 helen betekent dat je de lijn alvast kunt kleuren tot aan de 2. Daarna ga je tellen: de breuk moet na het 2e stukje staan. Dan ben je immers bij 2 2/5. Schrijf op die plek de breuk op de lijn:
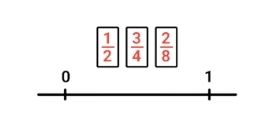
Soms heb je maar 1 getallenlijn en moet je daar verschillende breuken op plaatsen. Hoe je dát doet, gaan we je laten zien. Kijk, je hebt hier 1 getallenlijn en daar moeten de breuken 1/2, 3/4 en 2/8 op geplaatst worden.
Als je naar deze breuken kijkt, valt je misschien iets op. Zie jij het ook? Deze breuken kun je gelijknamig maken! Je kunt namelijk van alle 3 de breuken achtsten maken. Als je van 1/2 achtsten wilt maken, moet je de noemer (2) x 4 doen. 2 x 4 is namelijk 8. Dat houdt in dat je de teller (1) ook x 4 moet doen. Dan krijg je 4/8.
Hetzelfde doen we met de andere breuken:
1/2 = 4/8
3/4 = 6/8
2/8 = 2/8
Aan die laatste breuk hoef je dus niets meer te doen. Nu wordt het plaatsen van de breuken op de getallenlijn ineens een heel stuk gemakkelijker. Je hoeft de lijn nu nog maar 1 keer in 8 stukken te verdelen. Daarna zet je heel eenvoudig de breuken op de juiste plek: achter het 2e deel, achter het 4e deel en achter het 6e deel.
Let wel goed op! De opdracht was om 1/2, 3/4 en 2/8 op de lijn te zetten. Schrijf daarom op de lijn geen 4/8, maar 1/2. En schrijf niet 6/8, maar 3/4, want dat was de opdracht. 2/8 kun je wel zo opschrijven.


Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 6 (Gratis)

Oefenbladen Rekenen Groep 7 (Gratis)
Breuken op getallenlijn groep 8
In groep 8 maakt de leerkracht het nog een beetje moeilijker voor je. Zo moet je breuken om kunnen zetten in decimalen. Ook moet je breuken die je niet gelijknamig kunt maken op een getallenlijn plaatsen. Daar geven we nu een voorbeeld van.
Op de volgende getallenlijn moet je de breuken 1/5, 2/3 en 5/7 plaatsen. Deze breuken kunnen niet gelijknamig gemaakt worden.
Hoe pak je deze som dan aan? Eigenlijk is het niet zo moeilijk. Je verdeelt de getallenlijn gewoon op 3 verschillende manieren in stukken. Je hebt tenslotte 3 verschillende noemers. Het is in zo’n geval handig om met kleurtjes te werken. Dan zie je beter wat je doet. Voor 1/5 verdeel je de lijn in 5 stukjes. Na het 1e stukje zet je dan 1/5 deel neer.

Vervolgens zet je 2/3 op de lijn. Neem daarvoor een andere kleur. Je moet dezelfde lijn nu in 3 stukken verdelen… De breuk 2/3 ligt dan direct achter het 2e stukje.

Als laatste neem je een derde kleur voor de breuk 5/7. Je verdeelt de lijn in 7 stukken en zet 5/7 nu op de lijn achter het 5e stukje. De getallenlijn ziet er nu zo uit:

Zo, nu staan de 3 verschillende breuken op 1 getallenlijn. Als je de kleurtjes weghaalt of uitgumt, ziet de getallenlijn er weer heel netjes uit:
Werk stap voor stap
We hebben je laten zien hoe je breuken op een getallenlijn moet zetten.
Je weet nu:
- hoe je een breuk op de juiste plek op de getallenlijn moet zetten;
- hoe je op de getallenlijn afleest welke breuk bij de pijl moet staan;
- waar je gemengde breuken op een getallenlijn moet plaatsen;
- hoe je breuken met verschillende noemers op een getallenlijn moet plaatsen door ze gelijknamig te maken;
- hoe je met behulp van kleurtjes breuken met verschillende noemers op een getallenlijn plaatst als ze niet gelijknamig gemaakt kunnen worden.
Het belangrijkste met dit soort sommen is altijd dat je stap voor stap werkt. Kijk eerst welke stappen nodig zijn om tot de oplossing te komen.
Soms hoef je maar weinig stappen te zetten. Dat is bijvoorbeeld het geval als je maar 1 breuk hoeft te plaatsen. Als je meerdere breuken moet plaatsen, controleer dan altijd of je ze gelijknamig kunt maken. Lukt dat niet, dan gebruik je verschillende kleurtjes om de getallenlijn op verschillende manieren in stukken te verdelen.
We vinden het natuurlijk heel belangrijk dat jij de stof echt goed gaat beheersen. Daarom vind je onder dit artikel een werkblad, waarmee je lekker kunt oefenen. Heb je nog vragen of wil je vertellen hoe jij breuken op een getallenlijn zet? Plaats hieronder gerust een reactie!
Breuken getallenlijn werkblad
Maak de volgende opgaven. Alle antwoorden vind je onderaan deze pagina.
Opdracht 1
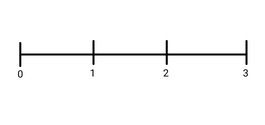
Plaats de breuken op de juiste plaats binnen de getallenlijn.
- 1/4

2. 5/6

3. 2/5

4. 2 5/8
5. 1 2/5

Opdracht 2
Welke breuk hoort op de plaats van het pijltje?
1.

2.
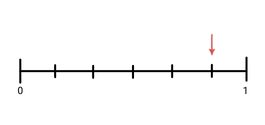
3.

4.
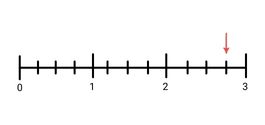
5.
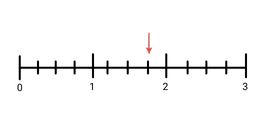
Opdracht 3
Plaats de verschillende breuken op de juiste plaatsen binnen de getallenlijn. Teken de getallenlijn zelf.
- 1/3, 2/3 en 5/6
- 1/2, 3/5 en 7/10
- 2/5, 1/7 en 4/6
Antwoorden opdracht 1
- 1/4
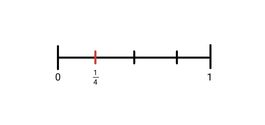
2. 5/6
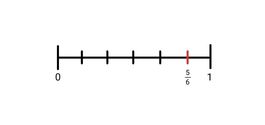
3. 2/5
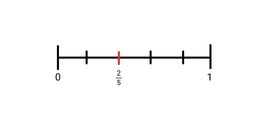
4. 2 5/8
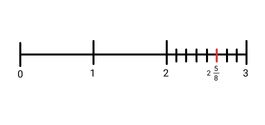
5. 1 2/5
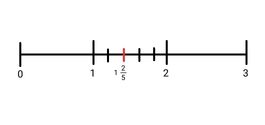
Antwoorden opdracht 2
- 3/6 = 1/2
- 5/6
- 3/10
- 2 3/4
- 1 3/4
Antwoorden opdracht 3
- 1/3, 2/3 en 5/6
Gelijknamig maken geeft: 2/6, 4/6 en 5/6

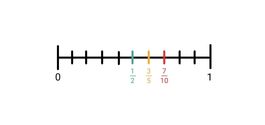
2. 1/2, 3/5 en 7/10
Gelijknamig maken geeft: 5/10, 6/10 en 7/10
3. 2/5, 1/7 en 4/6
Deze breuken zijn niet gelijknamig te maken.

Meer uitleg over breuken?
- Breuken optellen
- Breuken aftrekken
- Breuken gelijknamig maken
- Kleinste gemene veelvoud
- Procenten berekenen
- Breuken groep 6
- Deel van het geheel berekenen
- Zo gebruik je een breukenposter
-
Oefenboeken Doorstroomtoets Groep 8 deel 1 + deel 2
Oorspronkelijke prijs was: 54,00.39,95Huidige prijs is: 39,95. BUNDELKORTINGIn mijn winkelwagen Bekijk detailsJaarpakket Groep 8
Oorspronkelijke prijs was: 701,25.490,00Huidige prijs is: 490,00. Speciaal JaarpakketIn mijn winkelwagen Bekijk detailsRekenpakket Groep 6 – 2e helft schooljaar (Lib/Cito-IEP)
Oorspronkelijke prijs was: 59,90.47,00Huidige prijs is: 47,00. Aanbieding!In mijn winkelwagen Bekijk detailsCito E6 – IEP groep 6 pakket (2e helft schooljaar)
Oorspronkelijke prijs was: 59,90.47,00Huidige prijs is: 47,00. Aanbieding!In mijn winkelwagen Bekijk detailsGerelateerde artikelen
Reacties
Eén reactie op “Breuken op de getallenlijn plaatsen: uitleg en voorbeelden”Geef een reactie












Perfect