Getallenlijn maken: help je kind de sommen begrijpen (+ voorbeelden)


Rekenen is een grote ontdekkingstocht, gevuld met bijzondere ontmoetingen met cijfers, structuren en oplossingsstrategieën….
“Ja, ja..” zal je misschien zeggen. “Vooralsnog zit ik met een kind dat heel veel moeite heeft met het maken van het rekenhuiswerk.” Misschien kun je een getallenlijn maken om je kind te helpen.
Als je kind rekenproblemen ervaart, vindt het vaak de rekenopgaven niet leuk. Sommige kinderen hebben om deze reden zelfs een hekel aan rekenopdrachten, zowel thuis als op school. Er zijn kinderen die ten aanzien van rekenen een negatief zelfbeeld of rekenangst ontwikkelen. Zij hebben vaak gedachten als: ik kan het niet, deze sommen zijn veel te moeilijk enzovoort. Deze gedachten hebben een negatieve invloed op het werkgeheugen. En juist dat werkgeheugen hebben deze kinderen hard nodig bij het oplossen van de rekenopdrachten.
Hoe leg ik sommen uit?
Hoe krijgt je kind meer plezier in rekenen? Door hem succeservaringen te bieden. Je wijst hem dan op de dingen die wel goed gaan en geeft daarvoor een compliment. Succeservaringen creëer je ook door het inzetten van hulpmiddelen bij het rekenen. Bijvoorbeeld de tafelkaart of de getallenlijn.
Het is voor een kind vaak verwarrend als het thuis een andere instructie hoort dan op school. Vooral als de sommen nieuw zijn en je kind de werkwijze nog niet geautomatiseerd heeft.
Vraag aan de leerkracht welke strategieën hij in de klas aanbiedt, zodat je deze thuis kunt herhalen en/of aanvullen.
Kinderen hebben er veel aan als je tijdens je uitleg veel voorbeelden geeft. Verwoord de som en denk hardop na over de manier waarop je de som gaat uitrekenen. Verwoord vervolgens je handelingen en schenk daarbij aandacht aan de deelstappen waarmee je tot de uitkomst van de som komt. Met een getallenlijn visualiseer je deze handelingen.
Doel van de getallenlijn
In alle leerjaren van het basisonderwijs wordt de getallenlijn ingezet.
De getallenlijn heeft het volgende doel: je kind ontwikkelt begrip van hele getallen, breuken en kommagetallen, zodat hij weet (en automatiseert) wat het getal is en welke plaats het heeft op de getallenlijn.
Getallenlijn groep 3
Je kind ontwikkelt bij rekenen in groep 3 begrip van de getallen tot 20. Dit houdt in dat hij:
- de getallen globaal op de getallenlijn kan plaatsen;
- de getallen kan ordenen naar grootte;
- de getallen kan splitsen.
Daarna leert je kind de sommen met erbij (+, plus) en eraf (-, min) in opbouw: eerst tot 5, dan tot 10. In de tweede helft van groep 3 gaan de sommen tot 20. Eerst nog zonder overschrijding van het tiental en vervolgens met overschrijding van het tiental.
Bij deze leerdoelen krijgt je kind de volgende strategieën aangeleerd om sommen (tot 20) op te lossen. Dit zijn heel belangrijke basisvaardigheden waarop in de hogere groepen wordt voortgebouwd.
- Splitsen tot 10 (5 kun je splitsen in 2-3, 4-1, 5-0, 1-4, 3-2 en 0-5)
- Splitsen tot 20 (13 kun je splitsen in 11-2, 7-6, 3-10 enzovoort)
- Omvormen (5 + 7 = 6 + 6)
- Bijna dubbel (6 + 5 = 5 + 5 + 1)
- Verwisselen (2 + 7 = 7 + 2)
Je kind leert ook over ‘verliefde harten’ of ‘vrienden van…’. Hij weet dat 9 + 1 en 8 + 2 en 7 + 3 en 6 + 4 en 5 + 5 samen 10 zijn. Hetzelfde geldt voor combinaties die samen 20 vormen: 11 + 9, 12 + 8 enzovoort.
Met een getallenlijn oefenen
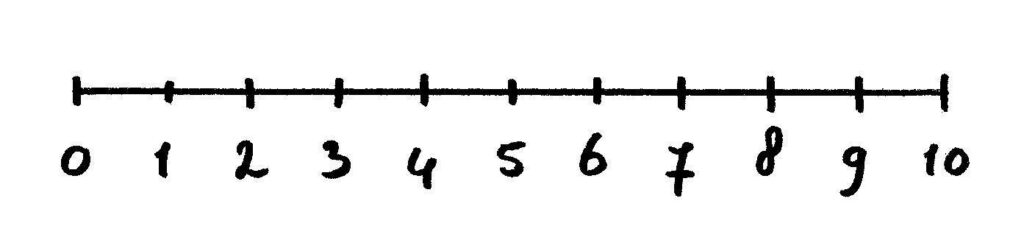
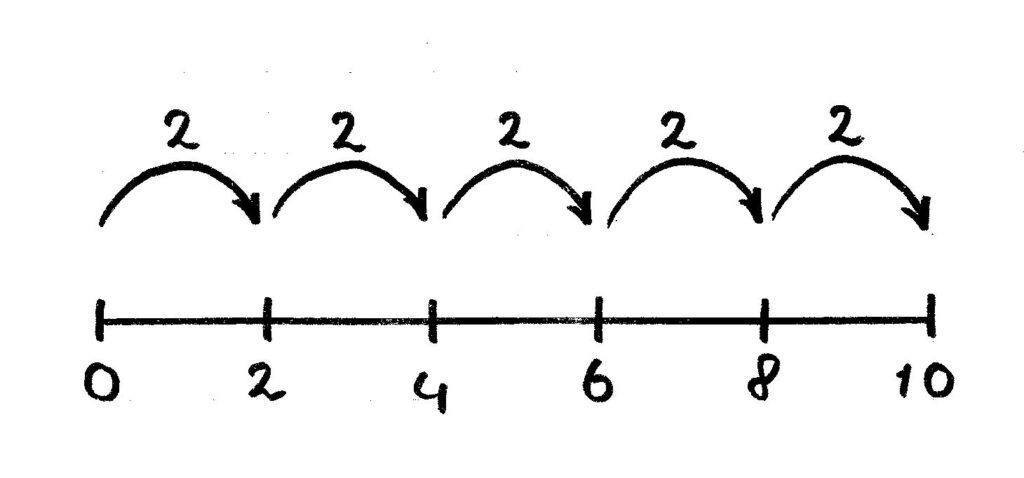
- ‘Verliefde harten’: deze strategie moet uiteindelijk een automatisme worden. 9 + 1 en 8 + 2 en 7 + 3 en 6 + 4 en 5 + 5 en andersom ☺. Op de getallenlijn ziet dat er zo uit:

- Splitsen tot 10: zet op de getallenlijn een zwarte streep bij het getal dat gesplitst wordt. Vervolgens zeg je: “6 kan gesplitst worden in 2 en …. ? (4)” Je maakt dit visueel door je woorden om te zetten in de handeling: je tekent van 0 naar 2 een boog en je vraagt je kind een boog te tekenen van 2 naar 6.
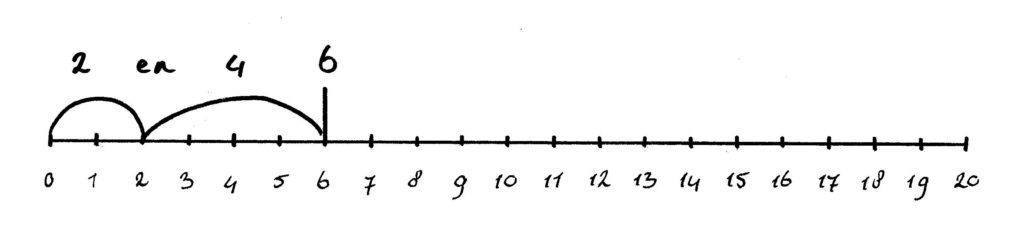
3 + 4 =
Je kind start bij 3, telt er 4 streepjes bij op en kijkt bij welk cijfer het terechtgekomen is. Dat cijfer is het antwoord:
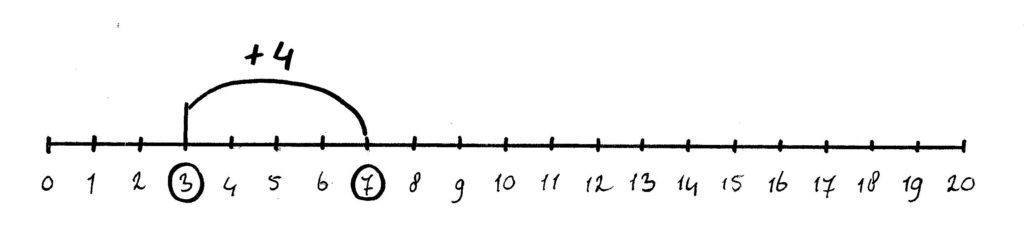
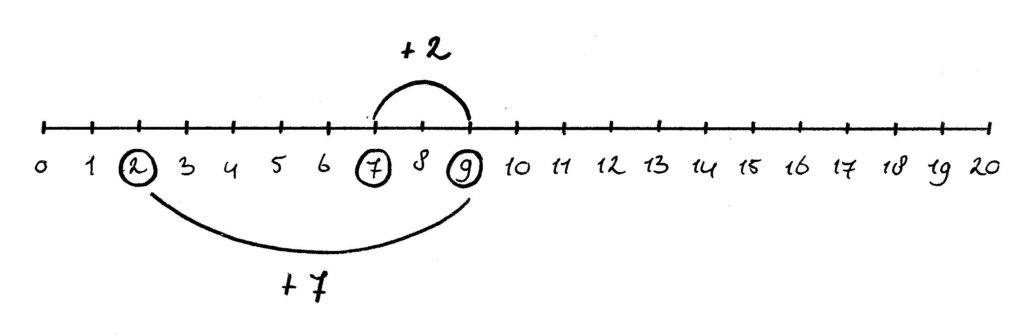
- Verwisselen: Dit is een handige strategie bij het toekomstige hoofdrekenen. De volgende som is daar een voorbeeld van:
2 + 7 = (7 + 2)
Je kind start bij 7, telt er 2 streepjes bij op en kijkt bij welk cijfer het terechtgekomen is.
Laat nog wel zien dat 2 + 7 hetzelfde antwoord geeft, maar dat ‘verwisselen’ een makkelijkere manier is. Je begint dan namelijk met het hoogste getal en hoeft dus minder te tellen.
Getallenlijn tot 20

Met behulp van de getallenlijn worden sommen tot 20 (eerst zonder overschrijding van het tiental, dan met overschrijding van het tiental) gevisualiseerd. Ook wordt uitgelegd dat de cijfers 11 tot en met 20 een herhaling zijn van 1 tot en met 10, maar dan met een tiental ervoor.
De overschrijding van het tiental wordt met behulp van de getallenlijn inzichtelijk gemaakt. Daardoor is dit een goede voorbereiding op de sommen tot 100.
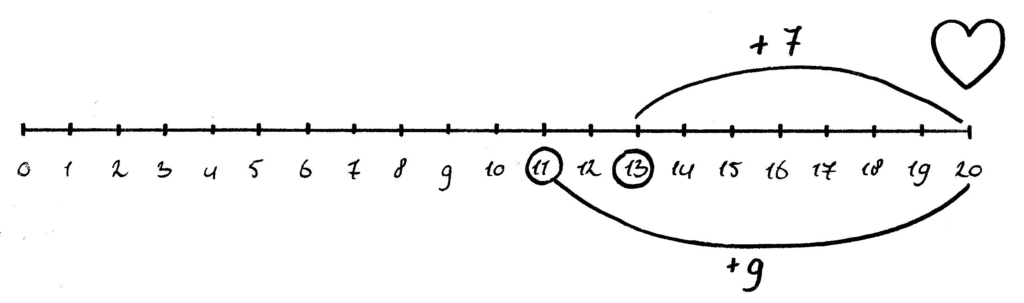
- ‘Verliefde harten’: deze strategie moet uiteindelijk een automatisme worden. 19 + 1 en 18 + 2 en 13 + 7 en 11 + 9 enzovoort.
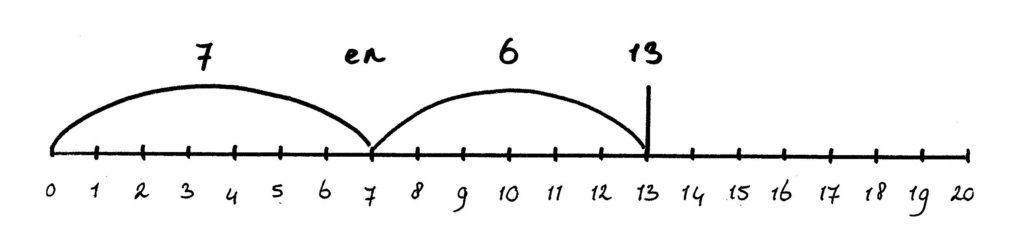
- Splitsen tot 20: zet op de getallenlijn een zwarte streep bij het getal dat gesplitst wordt. Vervolgens zeg je: “13 kan gesplitst worden in 7 en …. ? (6)” Je maakt dit visueel door je woorden om te zetten in de handeling: je tekent van 0 naar 7 een boog en je vraagt je kind een boog te tekenen van 7 naar 13.
De som 12 + 6 wordt op de volgende manier uitgerekend: 12 opzoeken op de getallenlijn, 6 erbij optellen en je kind heeft het antwoord. Wijs je kind op het volgende: wanneer het tiental gepasseerd wordt, komt er ook een tiental in het antwoord. Die 10 mag als het ware ‘meelopen’ tot 20… Je kunt dit met behulp van de splitsstrategie verduidelijken.
8 + 5 =
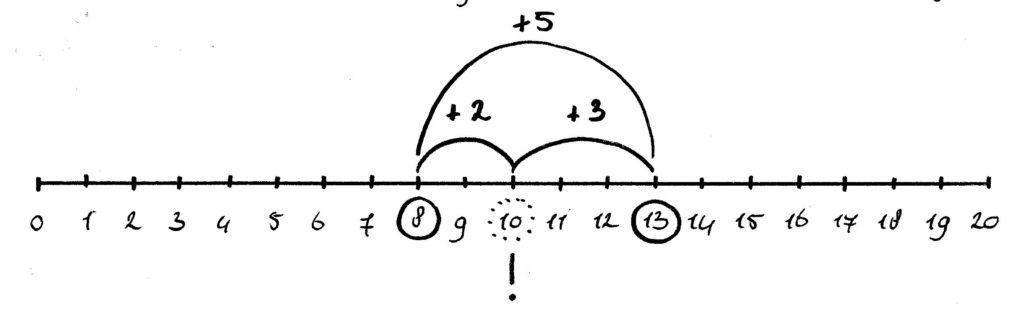
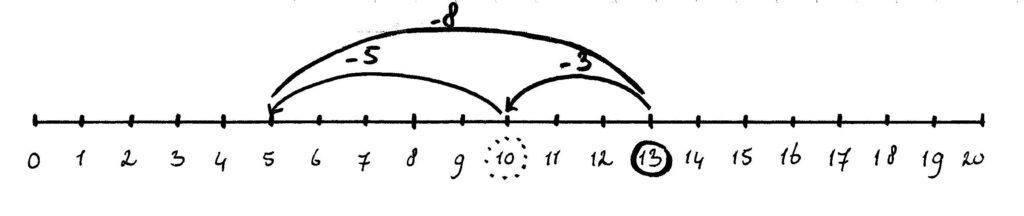
13 – 8 =
Bij minsommen start je samen met je kind bij 13. Eerst tel je 3 stapjes terug en dan (vanaf 10) nog 5 stapjes (8 splits je in 3 en 5). Het is in de eerste fase goed om stil te staan bij het passeren van het tiental. De tien die gezellig mee mocht lopen, moet bij de plaats van 10 achterblijven. De cijfers gaan zonder tiental van 9 terug naar 1.
Een lege getallenlijn
Zodra je kind laat zien dat het tot zover inzicht heeft in de sommen tot 20, is het moment aangebroken om een lege getallenlijn in te zetten. Een getallenlijn zonder getallen (met uitzondering van een begin- en eindcijfer) wordt een ‘lege’ getallenlijn genoemd.
Zo’n lege getallenlijn kan een vijfstructuur hebben. Op 5, 10 en 15 staat dan een streepje.
Veel kinderen hebben het nodig om gewezen te worden op de zogenaamde vijf- en tienstructuur. De vijf- en tienstructuur zijn verkorte vormen van uitrekenen en vormen daarmee een stap naar een volgende reken(denk)niveau.
6 + 3 =
Gelijk naar het streepje van de 5 + 1 en dan 3 erbij.


Getallenlijn groep 4
In groep 4 worden de sommen tot 10 geautomatiseerd. Dit wil zeggen dat je kind maar heel weinig tijd nodig heeft om tot het goede antwoord te komen. Het is als het ware een automatisme geworden. Je kind krijgt bovendien inzicht in de getalstructuur tot 100 en kan de getallen tot 100 vlot op de juiste plaats zetten op de getallenlijn. Met regelmaat krijgt je kind rekenopdrachten waarmee dit inzicht getraind wordt.
Getallenlijn tot 100

Net na de start van groep 4 worden sommen tot 100 aangeboden:
- plus- en minsommen met tientallen: 37 + 10, 37 + 30, 84 – 10, 84 – 20 enzovoort.
- plus- en minsommen tot 100 zonder overschrijding van het tiental: 42 + 7, 59 – 6 enzovoort.
- plus- en minsommen tot 100 met overschrijding van het tiental: 56 + 8, 67 – 9 enzovoort.
De vaardigheid splitsen die je kind in groep 3 geleerd heeft, komt nu bijzonder goed van pas. Bij alle bovengenoemde sommen kan je kind de getallenlijn gebruiken.
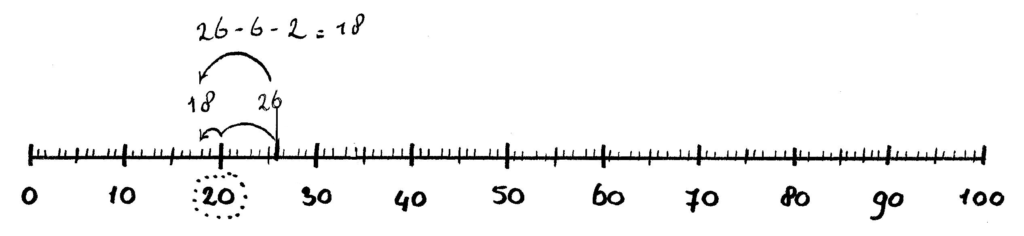
- Splits-aanpak: ook wel ‘rekenen via een tiental’ genoemd. Bijvoorbeeld: 26 + 8 = 26 + 4 + 4 of 26 – 8 = 26 – 6 – 2.

Er zijn rekenmethoden op scholen die de onderstaande splitsstrategie aanleren; de tientallen worden vóór het uitrekenen gesplitst van de eenheden. Dit is de voorbereiding op het kolomsgewijs optellen (groep 5). Helaas is deze manier voor veel kinderen nogal verwarrend. De getallenlijn is hierbij namelijk niet te gebruiken.
- Plussommen tot 100: 34 + 27, eerst de tientallen bewerken (30 + 20 = 50). Dan de eenheden bewerken: (4 + 7 = 11), vervolgens laat je je kind die bij elkaar optellen:
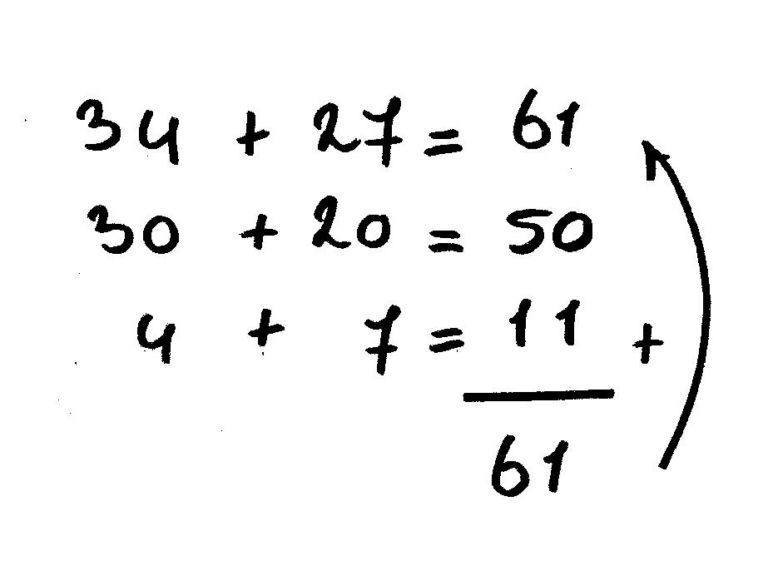
- Minsommen tot 100: 34 – 27, eerst de tientallen bewerken 30 – 20 = 10. Dan de eenheden bewerken 4 – 7 = -3. Vervolgens laat je je kind die van elkaar aftrekken (10 – 3 = 7).
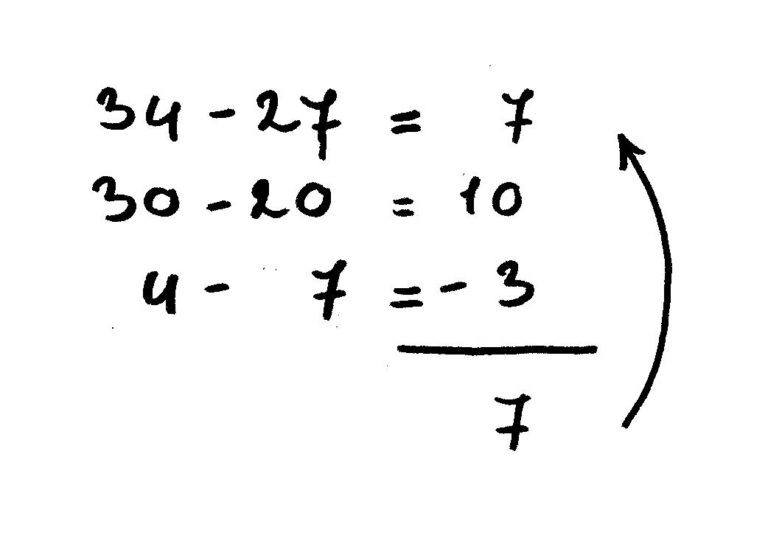
- Rond-getal-aanpak, ook wel handig rekenen of compenseren genoemd:
Bijvoorbeeld: 26 + 38 → je maakt van 38 even 40 → 26 + 40
Je hebt er 2 te veel bijgedaan, die moeten er weer af → 26 + 40 – 2
Nog een voorbeeld: 67 – 19
Je maakt van 19 even 20 → 67 – 20
Je hebt er 1 te veel afgehaald, die moet er weer bij → 67 – 20 + 1
Hierbij is de getallenlijn, als ondersteuning, goed te gebruiken. - Aanvullen (alleen bij eraf-sommen): 50 – 48 kun je handig uitrekenen door het verschil uit te rekenen: hoeveel ligt er tussen 48 en 50? Ook hierbij is de getallenlijn, als ondersteuning, goed bruikbaar.
- De rijgaanpak: 34 + 27 reken je uit door eerst bij 34 de 2 tientallen van 27 op te tellen → 34 + 20 = 54 en dan bij 54 de eenheden op te tellen → 54 + 7 = 61. In veel rekenmethoden wordt de rijgstrategie het meest aangereikt. Deze strategie vormt namelijk een goede voorbereiding op het hoofdrekenen.

Weerstand tegen het gebruik van een getallenlijn
Wanneer je kind gewend is aan de lege getallenlijn, zal het op een gegeven moment ook de beperking ervan ervaren. De getallenlijn hielp eerder om inzicht in de som te krijgen, maar je kind zal al snel merken dat werken met de getallenlijn ook heel bewerkelijk en tijdrovend is. Geef je kind dan ook de ruimte om de sommen uit het hoofd uit te rekenen of bijvoorbeeld alleen de tussenstappen te noteren. De leerkracht noemt dit de stap naar formeel rekenen en daar is het per slot van rekening allemaal om begonnen.
Getallenlijn groep 5
In groep 5 worden sommen tot 1000 geleerd. Ook nu geldt weer dat je kind eerst inzicht moet krijgen in de getalstructuur tot 1000. Ook moet het de getallen tot 1000 vlot op de juiste plaats weten neer te zetten. Een getallenlijn is hierbij een handig hulpmiddel.
Getallenlijn tot 1000
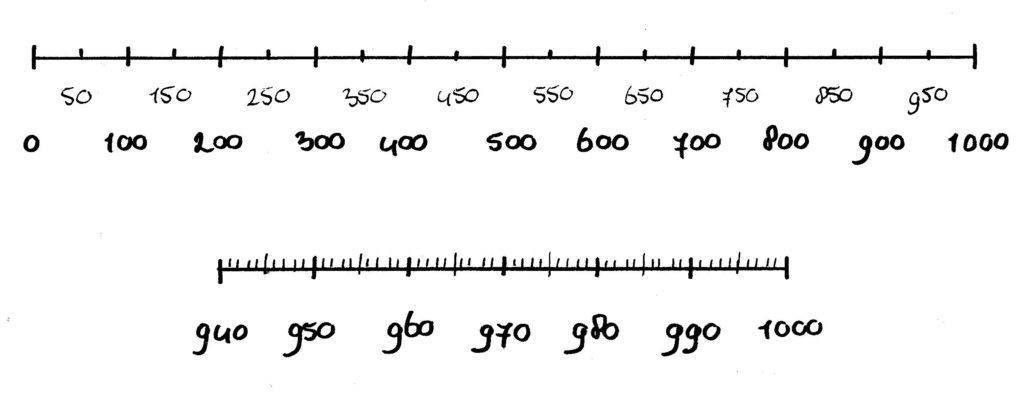
Om sommen tot 1000 uit te rekenen, worden in de klas verschillende strategieën aangereikt. Zo heb je:
- hoofdrekenen
- schattend rekenen
- kolomsgewijs rekenen
- cijferend rekenen
Bij hoofdrekenen en schattend rekenen kan je kind zelf kiezen voor een bepaalde strategie om tot het antwoord te komen. Voor kolomsgewijs rekenen en cijferend rekenen is er een vaste strategie waarmee je kind de sommen moet uitrekenen.
Als je kind die 2 strategieën door elkaar gebruikt, levert dat veel verwarring op. Waar hij bij cijferend rekenen altijd met de eenheden start, dan de tientallen uitrekent en dan de honderdtallen, moet hij bij kolomsgewijs rekenen juist met de honderdtallen starten en werkt hij terug naar de eenheden.
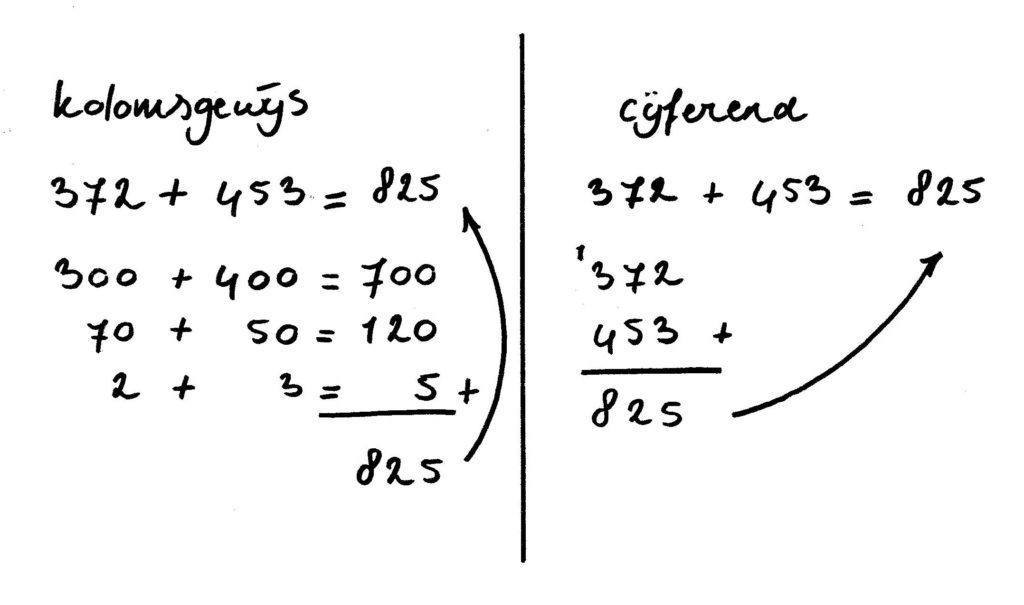
Getallenlijn groep 6, 7 en 8
In groep 6 t/m 8 komt je kind voor het eerst in aanraking met kommagetallen. Ook worden breuken en kommagetallen verder uitgelegd en bewerkt. Allereerst is het belangrijk dat je kind inzicht krijgt in de structuur van de kommagetallen. Het gaat er dan vooral om dat je kind weet hoeveel een kommagetal waard is. Om daarin inzicht te krijgen is de getallenlijn erg goed te gebruiken.
Op de basisschool maakt je kind kennis met kommagetallen met tienden, honderdsten en duizendsten.
Kommagetallen op de getallenlijn
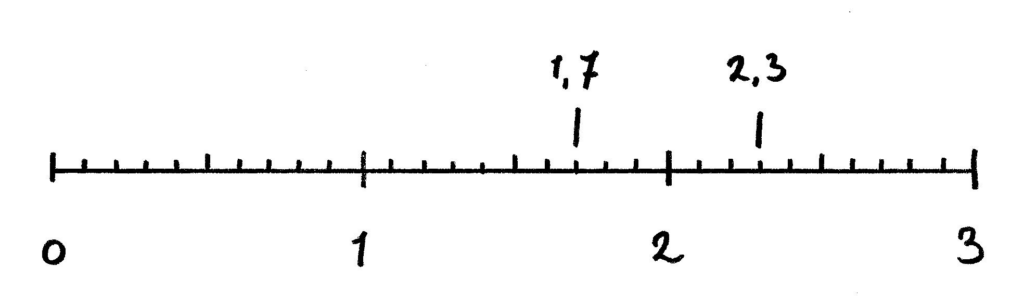
Met behulp van een getallenlijn ziet je kind snel dat het getal 1,7 tussen 1 en 2 ligt. Of dat 2,3 tussen de 2 en de 3 ligt. Je kunt met de getallenlijn eenvoudig uitleggen en laten zien dat tussen 2 hele getallen nog heel veel andere getallen liggen. Want 2,3 ligt tussen 2 en 3, maar 2,34 ligt bijvoorbeeld tussen 2,3 en 2,4.

Je kind zal al snel zien dat de afstand tussen 2 hele getallen onder te verdelen is in tienden. En dat de afstand tussen 2 tienden op zijn beurt weer onder te verdelen is in honderdsten. En dat de afstand tussen honderdsten weer onder te verdelen is in duizendsten.
Een getallenlijn is ook een handig hulpmiddel om kommagetallen bij elkaar op te tellen en van elkaar af te trekken met behulp van de rijgaanpak. Bijvoorbeeld: 1,1 + 1,6 = 2,7
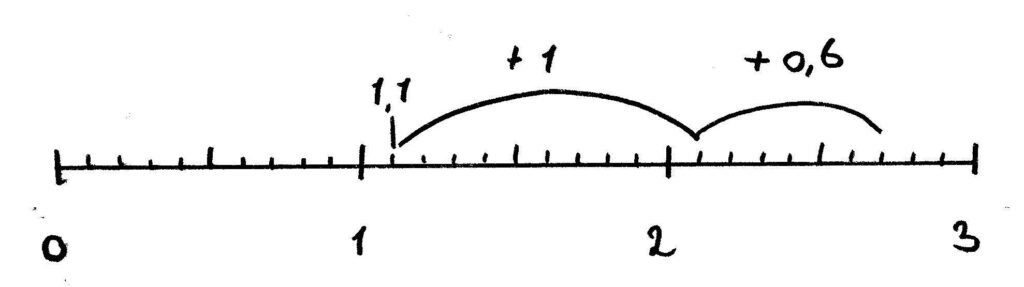
Sommen waarbij de getallen achter de komma niet gelijk zijn, zijn voor een kind makkelijker uit te rekenen wanneer hij de getallen gebruikt als geldbedragen. Zo telt je kind 0,45 en 0,6 makkelijker bij elkaar op als hij er € 0,45 + € 0,60 van maakt.
Er zijn overzichten waarbij de relatie tussen breuken, procenten en kommagetallen duidelijk wordt gemaakt. Het is erg handig als je kind die uit het hoofd te leert voor de Cito-toets!
Breuken op de getallenlijn
Een breuk zonder helen, waarvan de teller (het getal boven het deelstreepje) kleiner is dan de noemer (het getal onder het deelstreepje) is altijd kleiner dan 1. Je kind moet deze breuk dus altijd tussen de 0 en de 1 plaatsen.

Vertel je kind dat hij, wanneer hij breuken op een lege getallenlijn moet plaatsen, eerst de tussenliggende vakjes moet tellen. Dan weet hij waar de getallenlijn in onderverdeeld is (en dus wat de noemer is).
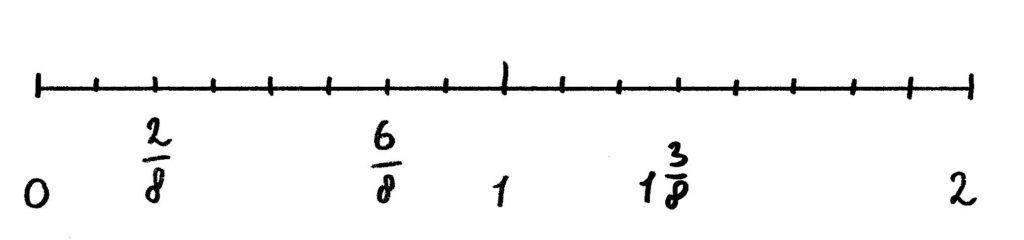
Rekenen is een grote ontdekkingstocht, gevuld met bijzondere ontmoetingen met cijfers, structuren en oplossingsstrategieën…. En…. als rekenen even lastig is? Herhaal dan de strategieën van groep 3 en observeer welke van die strategieën nog moeilijk zijn voor je kind. Oefen ze een aantal weken, want deze kennis is de basis!
Hopelijk draagt bovenstaande uitleg bij aan meer rekenplezier.
Succes!
Bekijk ook:







Hele goed
super al die uitleg mijn zoon in groep 5 scoort alleen onvoldoende bij alle reken opdrachten ik ga aan de slag. harstikke bedankt! graag nog meer ideeen.
De uitleg is een enorme hulp om met mijn zoon te oefenen en zoals Ron dat heeft aangegeven, zal het geweldig zijn om een pdf versie beschikbaar te stellen.
In mijn bijlespraktijk leidt één aangegeven methode hier boven, het werken met negatieve getallen, nagenoeg altijd tot een foute, hardnekkig ingesleten rekentechniek.
34 – 27 = ..?..
30 – 20 = 10
4 – 7 = 3 (!!!) Er staat dus géén -3…(min 3).
10 – 3 = 7
Kinderen laten het minteken al snel weg en dat valt dan jarenlang niemand meer op, omdat er uitsluitend naar het “goede antwoord” wordt gekeken.
Als kinderen zèlf nakijken, komt het al helemáál nooit meer boven water.
Daardoor schrijven kinderen in mijn huiswerk zonder problemen ook: 15 – 19 = 4 en
23 – 28 = 5
Bij gebrek aan controle van oplossingstechnieken ontstaan verder ook 5 : 10 = 2 en
7 : 21 = 3
Gebruik van de getallenlijn…
Volkomen met Maaike eens dat het zichtbaar maken van sommen bij het aanleren heel verhelderend werkt.
Mijn rekenleerlingen werken op geplastificeerde, grote getallenlijnen waarop ze de sommen met whiteboardstiften moeten intekenen. (En hardop verwoorden.)
Een oude schoolmeesterskreet zegt: “Rekenen is tekenen.”
Beste Peter,
Dank voor je aanvulling!
Hartelijke groet,
Carola
Met deze methode wordt het heel erg duidelijk voor de kinderen, ze kunnen het beter visualiseren, en vinden het een stuk leuker. Zou ook graag de pdf versie willen ontvangen.
Beste Rob,
Dank voor je bericht en compliment.
Onderaan het artikel kun je het PDF-bestand downloaden.
Hartelijke groet,
Carola de Koning
Alle toelichtingen en uitleggen helpen enorm. Is het mogelijk dat aan het einde van elke toelichting ook de pdf versie beschikbaar wordt gesteld?
Beste Ron,
Fijn om te horen!
Onderaan het artikel kun je het PDF-bestand downloaden.
Hartelijke groet,
Carola