
Misschien heb je tot op dit moment je kind enthousiast kunnen helpen met de ‘gewone’ sommen, maar laat je zelfvertrouwen je in de steek als het gaat om procenten, breuken en kommagetallen. Want hoe zat dat ook alweer met het regeltje: delen door een breuk is vermenigvuldigen met het omgekeerde?
Teller, noemer, gelijknamig maken….. hoe werkt dat ook alweer? En wat hebben breuken ook alweer te maken met procenten en kommagetallen? Wat maakt deze onderwerpen zo lastig?
Kinderen komen nogal eens met deze onderwerpen in de problemen, omdat er in de rekenmethoden te weinig tijd wordt ingepland voor de basis. Er wordt snel uitgelegd wat breuken zijn en wat ze te maken hebben met procenten en kommagetallen. Je kind krijgt alleen niet altijd de kans deze stof ook echt te begrijpen.
Al tijdens het rekenen in groep 2 wordt gestart met het aanbrengen van begrip voor hoeveelheden van hele getallen. Tot en met groep 3 worden getallen gekoppeld aan concrete materialen (blokjes, kralenketting, rekenrek). Dat gebeurt tot bijvoorbeeld het getal 4 een begrip op zich wordt, en de meeste kinderen het niet meer nodig hebben om bij het rekenen een concrete voorstelling van de hoeveelheid te maken.
Download hier de (gratis) Werkbladen Breuken Groep 6/7/8

Oefenbladen Rekenen Groep 8 (Gratis)
Voor het leren rekenen met breuken zou ook veel meer tijd moeten worden gestoken in het concreet werken met materialen. Bijvoorbeeld totdat ook ¼ een op zichzelf staand iets is geworden. De stap naar de ‘kale’ sommen wordt te snel gezet, waardoor kinderen allerlei trucjes aanwenden om de som uit te rekenen.
¼ + ¼ kan dan net zo goed 2/8 of 1/16 zijn als 2/4. Het is maar welk trucje je gebruikt. Sommige kinderen zijn er erg goed in om de goede trucjes te gebruiken, maar vallen toch door de mand als ze bijvoorbeeld een som als 1 – 1/8 moeten uitrekenen. Daar voorzien de trucjes niet in. Als je dan vervolgens vraagt of ze de som kunnen tekenen (1 hele taart min 1/8 taart) zien ze het antwoord ineens.
Het Freudenthalinstituut zegt er het volgende over:
“Kennis van rekenregels is kwetsbaar als het niet op begrip is gebaseerd. Omgekeerd kan een leerling die het in een bepaalde situatie gewenste rekenregeltje niet kent, toch een heel eind komen met inzicht in breuken en verhoudingen”.
In dit artikel vertellen we je hoe jij kunt zorgen dat je kind bij het rekenen met breuken, procenten en kommagetallen geen trucjes gebruikt, maar de sommen goed oplost doordat het echt begrijpt waar het over gaat. Door veel te werken met materialen help je jouw kind om de verbanden tussen deze onderwerpen te doorgronden.
Daarbij is het belangrijk dat je kind zoveel mogelijk zelf ontdekt. Het begrip wordt dan groter en je kind onthoudt de stof dan makkelijker.
Bovendien: begin bij het begin, ook al zit je kind in groep 7 en is het tot nu toe allemaal goed gegaan met die breuken. Grote kans dat je kind tot op dat moment de ‘trucjes’ goed heeft kunnen onthouden, maar nu door de bomen het bos niet meer ziet. Je kind reageert misschien met: “Ja, dat weet ik allemaal al lang”. Vraag dan of hij het aan jou kan uitleggen. Daarmee help je je kind om de kennis die het heeft te ordenen. Vaak kan het dan daarna zelf de volgende stappen zetten.
Breuken: tellers, noemers en meer
We beginnen bij de breuken. Een breuk is altijd een deel van het geheel. Hoe klein het stuk is, ligt er natuurlijk aan in hoeveel stukken je het geheel verdeelt. Dat kun je zien aan de noemer. Dat is het getal achter de schuine streep (of onder de horizontale streep).
¼ betekent dus 1 stuk van een taart die in 4 stukken is verdeeld. Als je 2 van die stukken hebt, heb je dus 2 van de 4, dus 2/4. De 2 is dan de teller, die vertelt hoeveel stukken je hebt. Je kunt dit in het dagelijks leven volop oefenen met etenswaren en snoep.
- Deel de rookworst/pizza/koek/reep/ovenschotel in 3, 4 of 5 stukken. Leg de
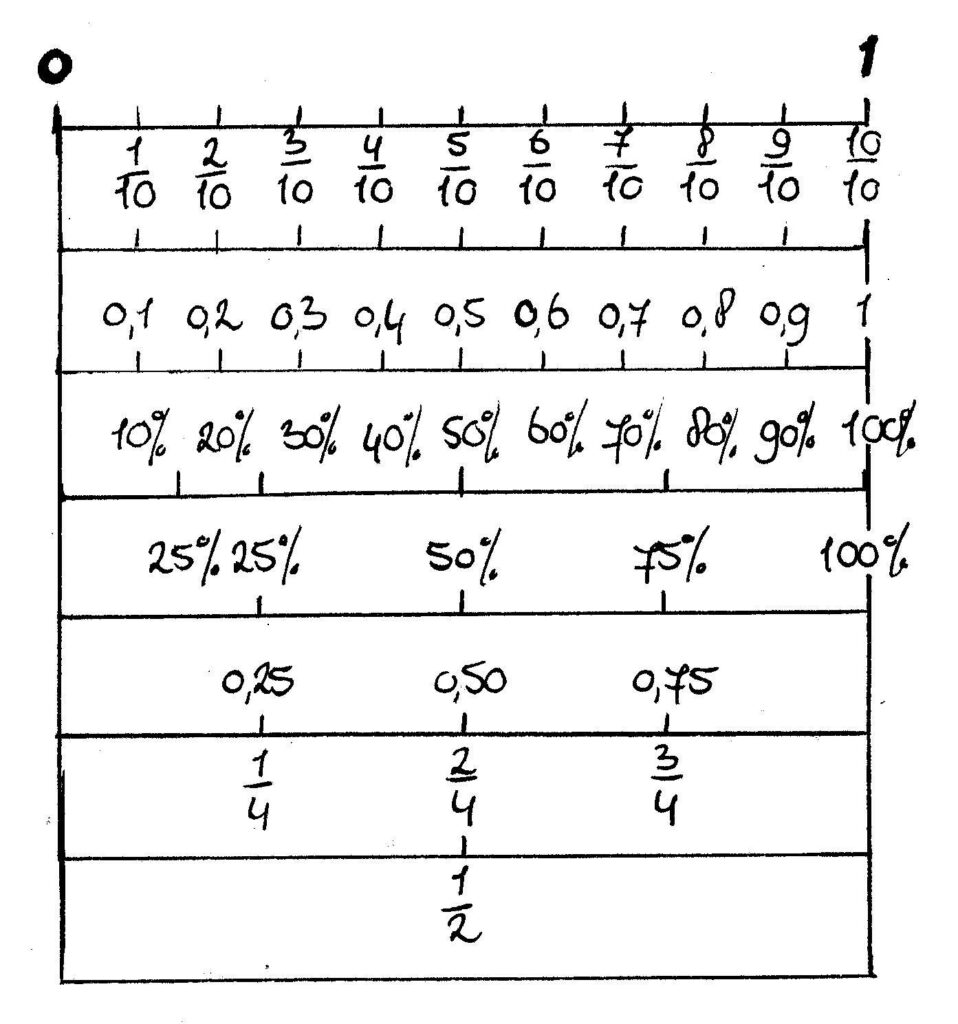
koppeling: 1 van de 3 stukken is hetzelfde als 1/3. - Stimuleer je kind om zelf andere kennis over breuken te ontdekken. Vraag bijvoorbeeld hoe je die taart/worst het beste in 4, 5 of 6 stukken kunt verdelen. En hoe krijg je 10 even grote stukken? Hoe heten die stukken? Door hier veel mee te oefenen, gaat je kind vanzelf zien dat 1/5 dus net zo groot is als 2/10, en 5/10 even groot als ½. Het ziet dan ook dat als je de stukken 2 keer zo klein maakt, je er dan ook zo 2 keer zoveel van hebt. Op dat moment kan het breuken omrekenen met het ‘’trucje’: als je de noemer en de teller met hetzelfde getal vermenigvuldigt, krijg je een breuk die gelijk is aan de eerste. Bijvoorbeeld: 1/3 is gelijk aan 2/6.
- Benoem de breuken ook regelmatig als 1 van de 5, 2 van de 10 is evenveel als 1 van de 5 enzovoort.
- Maak er ook sommen mee: 1/5 + 2/5 enzovoort, zodat je kind gaat snappen dat je dan alleen de tellers moet optellen en dat de noemer hetzelfde blijft. Als dat goed gaat, kun je ook vragen hoeveel dan 2/10 + 1/5 is, of 1/10 + 2/5. Ga daarbij ook over de helen heen, dus bijvoorbeeld 5/8 + 6/8. Laat je kind het tekenen en laat het zelf ontdekken dat je dan dus 1 hele taart hebt en 3 stukken van 1/8. Dus 1 3/8.
- Je kunt nu ook keersommen maken met breuken: hoeveel is 2 x 1/6, 3 x 2/8. Laat het je kind het steeds tekenen om het te ‘bewijzen’, ook al weet het gelijk het antwoord.
- Als je kind dit allemaal goed snapt, en de tellers en de noemers niet meer door elkaar haalt, kun je een stapje verder gaan. Vraag je kind bijvoorbeeld 25 plakjes champignons eerlijk te verdelen over een pizza die in 5 stukken is verdeeld. Je kind zal dan waarschijnlijk spontaan die 25 delen door 5. Maak de koppeling: 1/5 van 25 is dus 5.
Wat het hier verwarrend maakt, is dat 1/5 van 25 ook wordt geschreven als 1/5 x 25 of 25 x 1/5. Dan wordt iets wat je eerst uitrekent door te delen opeens als een vermenigvuldiging opgeschreven. Maar de uitkomst blijft natuurlijk hetzelfde: 25 stukken van 1/5 pizza is hetzelfde als 25/5 pizza en dat zijn 5 hele pizza’s. Laat je kind dat ook ‘bewijzen’ door het te tekenen! 1/5 x 25 is dus hetzelfde als 1/5 van 25.
Dit is een belangrijk inzicht. Oefen er vaak mee!
Herhaal sowieso deze sommen regelmatig met alles wat je maar kunt bedenken, zowel met ronde vormen als rechthoekige. Als dit allemaal gesneden koek is voor je kind, kun je de stap zetten naar de kommagetallen.
Van breuken naar kommagetallen
Met kommagetallen heeft je kind natuurlijk al lang kennis gemaakt bij het geldrekenen. Wat maakt die kommagetallen dan zo moeilijk als er mee gerekend moet worden buiten de context van geld? Dat komt omdat je kind heeft geleerd dat € 0,10 uitgesproken moet worden als 10 cent. De komma dient er dan dus alleen voor om de hele euro’s en de centen te onderscheiden. Maar als het euroteken er niet staat, wat betekent die 10 dan? Tijd voor weer een uitleg met iets lekkers!
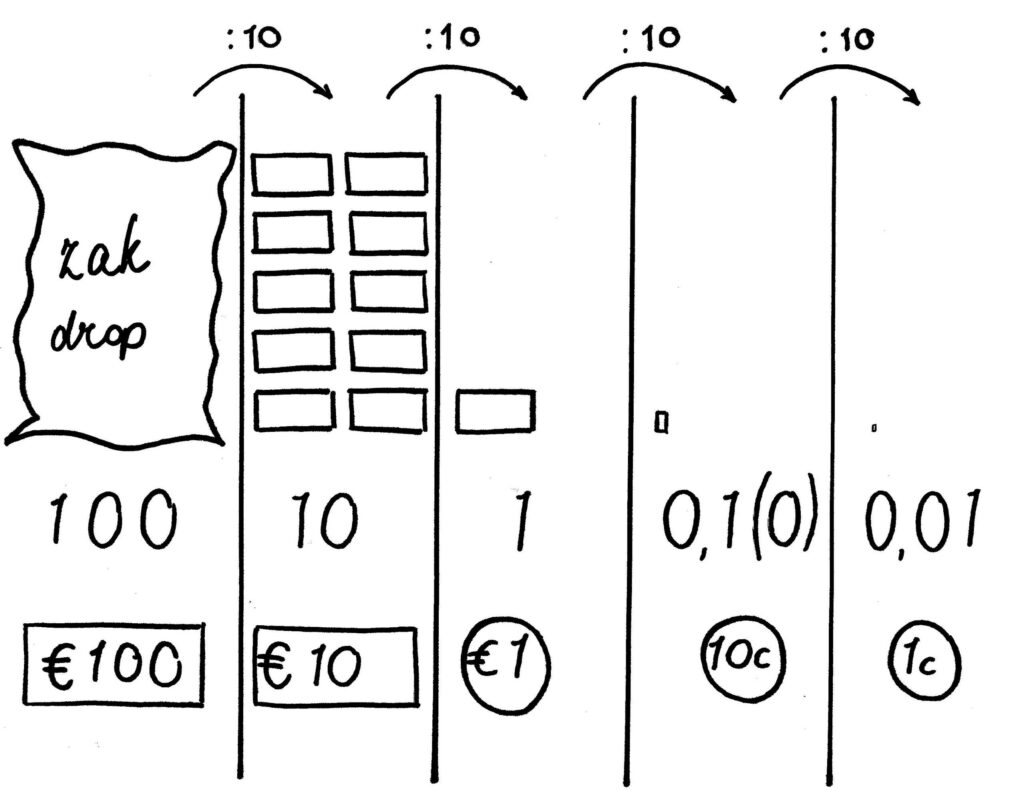
- Pak een zak met bijvoorbeeld zachte dropjes, het liefst rechthoekige. Zeg dat er 100 dropjes in de zak zitten, pak er 10 uit en legt ze op een blad papier. Schrijf er 10 onder. Je hebt die 100 dropjes door 10 gedeeld. Laat je kind de 10 dropjes door 10 delen. Leg 1 dropje neer, en zet er een 1 onder.
- Wat nu als je nog verder gaat delen? Dan heb je een mes nodig. Snijd het dropje in 10 stukjes en leg 1 stukje neer op het blad. Laat je kind zelf bedenken hoe je dit getal opschrijft. Komt het met 1/10? Prima! Laat het nadenken over hoe je dat als kommagetal kan schrijven. Komt het er niet uit? Vergelijk het dan met geld. Wat past er 10 keer in 1 euro? Hoe schrijf je dat? Juist, als € 0,10. Was 0,1(0) gelijk het antwoord op de eerste vraag, laat dan zien dat het ook 1/10 (1 van de 10) is.
Snijd tot slot het kleine stukje drop in 10 stukjes. Hoeveel van die stukjes passen er in tien eurocent met geld? Het verband is nu gelegd. Het eerste getal achter de komma geeft aan hoeveel tienden er zijn, het tweede hoeveel honderdsten. Je kind begrijpt nu dat een kommagetal ook altijd een deel van een geheel aangeeft, net als de breuken dat doen. - Ga op verpakkingen op zoek naar kommagetallen. Wat betekenen deze? Geven ze ook een deel van een geheel aan? En wat is dat geheel dan? Waar kun je dat aan zien? Bijvoorbeeld 0,98 kg op een pakje ham betekent 98/100 van een kg. 0,5 l betekent 5/10 van een liter.
- Hoe reken je breuken nu om naar kommagetallen? Dit kun je dus doen door steeds de verbinding te leggen tussen de breuken en geld, en van geld naar het ‘kale’ kommagetal.
- Geef je kind een euro en zeg dat die verdeeld moet worden tussen in totaal 5 kinderen. Hoeveel krijgt ieder? Je kind schakelt waarschijnlijk moeiteloos over van 1 euro naar 100 cent, en deelt dan 100 door 5. Dat is 20 cent en dat schrijf je als € 0,20. Ieder kind krijgt 1/5. 1/5 kun je dus schrijven als 0,20.
- Zo kun je alle breuken omrekenen naar kommagetallen. Start weer steeds bij de euro. Laat je kind zelf bedenken hoeveel ieder krijgt als je een euro deelt door 2, 3, 4 enzovoort. Zoveel cent, dus € 0,… . Je kind leert op school de meest voorkomende combinaties uit het hoofd, maar weet nu ook hoe het zelf het kommagetal kan vinden.

PDF schema breuken-procenten-kommagetallen
Leg nu weer het verband tussen de dropjes (kommagetallen), breuken en geld.
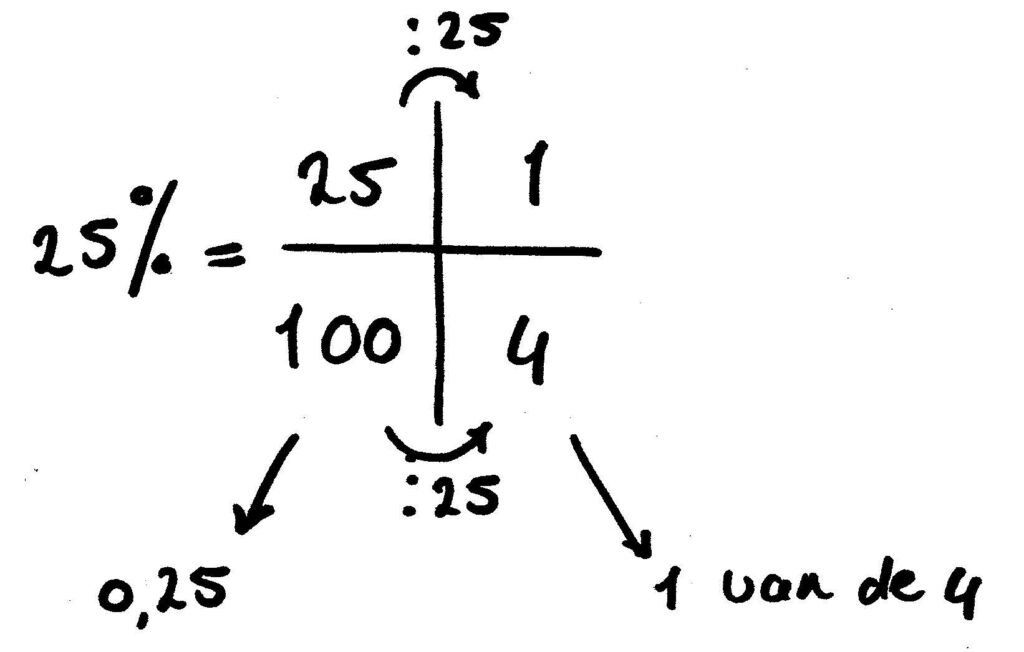
- Dat kleine stukje drop was er 1 van de 10. Je schrijft dat als 1/10 maar dus ook als 0,1(0). Het eerste getal achter de komma geeft dus aan dat het om 1/10 deel gaat. € 0,10 is ook 1/10 deel van 1 euro. € 0,01 is 1 cent, dat is 1/100 deel van 1 euro. Het tweede getal achter de komma geeft dus aan hoeveel honderdsten er zijn. 25 cent is dus 25 honderdsten van een euro. 0,25 is dus 25 honderdsten oftewel 25/100.
Bekijk het volgende schema met je kind om het allemaal nog wat duidelijker te maken, maar doe dit pas nadat je het zelf de verbanden hebt laten ontdekken.
Van kommagetal naar procenten
Deze stap is eigenlijk de makkelijkste stap, als al het voorgaande goed begrepen is. We hebben gezien dat je € 0,01 uitspreekt als 1 cent, maar dat het dus ook betekent: 1/100 deel van 1 euro. 0,01 kun je, los van de geldcontext, uitspreken als nul komma nul één, maar ook als 1/100. Procent betekent oorspronkelijk: per honderd.
Op school leert je kind eerst rekenen met ‘mooie percentages’ door deze te behandelen als een deler: als je 10% van iets moet uitrekenen, moet je dat delen door 10. 20% is dan het dubbele en 5% de helft, enzovoort. Om later ook 3% of zelfs 2,1% van iets te kunnen uitrekenen, is
het belangrijk dat je kind ook begrijpt hoe het zit:
- Pak het geld er weer bij. 10 procent kun je vergelijken met 10 cent. Dat gaat 10 keer in 1 euro (het geheel).
- 10 cent, 0,10, is dus hetzelfde als 1/10. Om dat uit te rekenen kun je dus ook het geheel delen door 10. Van daaruit kun je dus een heleboel percentages uitrekenen, door te verdubbelen, bij elkaar te tellen (10% + 10% + 10% + 5% = 35%). Je kind leert ook: 50% is altijd de helft en 25% is daar weer de helft van enzovoort. Maar hoe zit het dan met die 3%? Dat is dus hetzelfde als 3/100. Als je 3/100 van iets moet uitrekenen, reken je eerst 1/100 uit, en dat doe je keer 3. Dit wordt heel inzichtelijk met een verhoudingstabel.
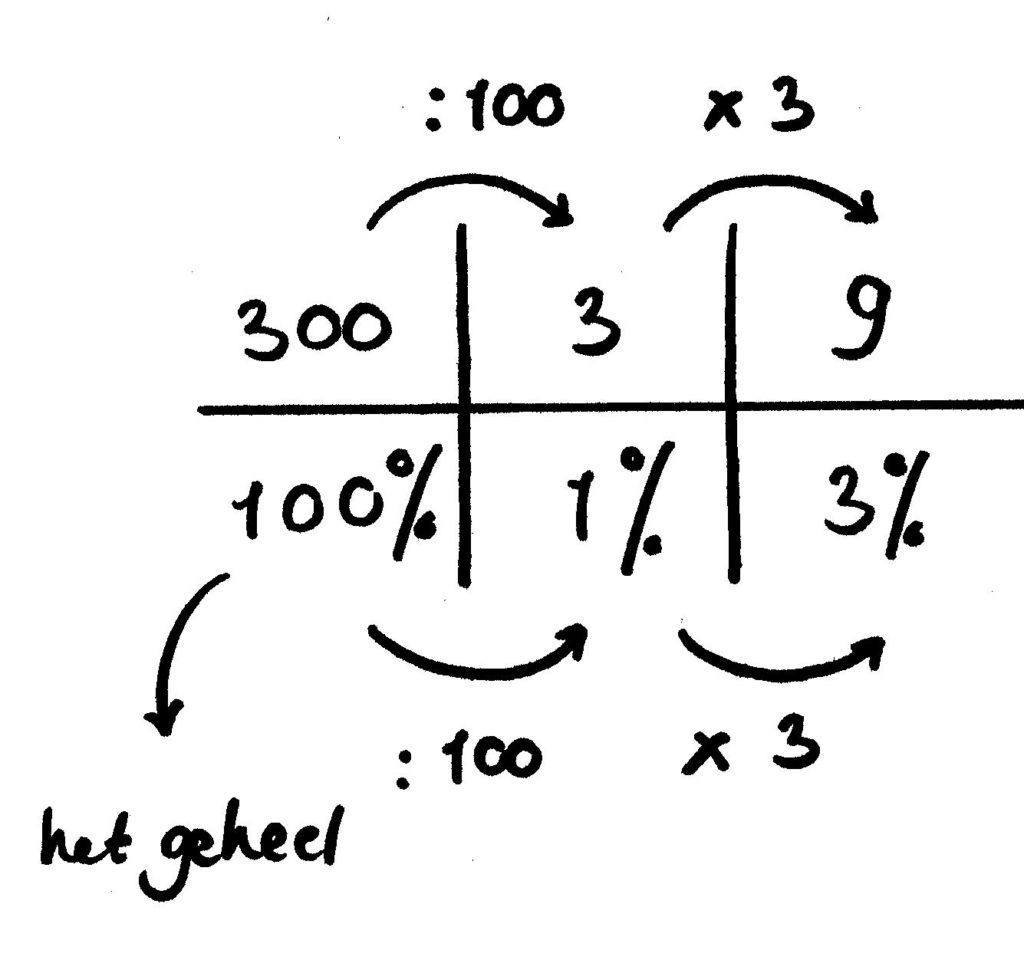
Oefenen met procenten? Klik hier om de Spoedcursus Procenten te bekijken.
Spoedcursus Procenten en kommagetallen Groep 7/8 (incl. Oefenboek)
Oorspronkelijke prijs was: 69,85.47,00Huidige prijs is: 47,00.
Bekijk ook:
- Procenten oefenen met de Nr. 1 formule
- Hoe bereken je procenten met een verhoudingstabel?
- Procenten berekenen, hoe doe je dat?
- Hoe bereken je een korting?
Bekijk ook deze video’s voor meer informatie over het omrekenen van breuken naar procenten en andersom:
Voor oefenen met breuken, procenten en kommagetallen in groep 7 en groep 8 kun je de volgende oefenboeken voor rekenen bestellen:
-
Oefenboeken Doorstroomtoets Groep 8 deel 1 + deel 2
Oorspronkelijke prijs was: 54,00.39,95Huidige prijs is: 39,95. BUNDELKORTINGIn mijn winkelwagen Bekijk detailsJaarpakket Groep 8
Oorspronkelijke prijs was: 701,25.490,00Huidige prijs is: 490,00. Speciaal JaarpakketIn mijn winkelwagen Bekijk detailsRekenpakket Groep 7 – 2e helft schooljaar (Lib/Cito-IEP)
Oorspronkelijke prijs was: 59,90.47,00Huidige prijs is: 47,00. Aanbieding!In mijn winkelwagen Bekijk detailsVideobijles Rekenen Groep 7
Oorspronkelijke prijs was: 79,00.49,95Huidige prijs is: 49,95. Aanbieding!In mijn winkelwagen Bekijk detailsBreuken en Procenten oefenpakket + videobijles (Cito – IEP)
Oorspronkelijke prijs was: 119,75.87,00Huidige prijs is: 87,00. BundelkortingIn mijn winkelwagen Bekijk detailsJaarpakket Groep 7
Oorspronkelijke prijs was: 595,00.490,00Huidige prijs is: 490,00. Speciaal JaarpakketIn mijn winkelwagen Bekijk detailsWil je liever breuken oefenen met Lego? Download hier de PDF.
Download gratis oefenbladen voor rekenen!
Meer uitleg over breuken?
- Breuken: een complete handleiding
- Breuken vereenvoudigen
- Kleinste Gemene Veelvoud
- Breuken delen
- Breuken gelijknamig maken
- Breuken optellen
OefenbladOefenbladen Rekenen Groep 8 (Gratis)
OefenbladOefenbladen Rekenen Groep 6 (Gratis)
OefenbladOefenbladen Rekenen Groep 7 (Gratis)
Gerelateerde artikelen
Reacties
23 reacties op “Van breuken naar procenten en kommagetallen: een handig schema (PDF)”Geef een reactie




















Super fijn!! Hartelijk dank!
Groetjes Faatje
Maaike,
vriendelijk dank voor je handige tips. Ik zal er zeker gebruik van maken.
Beste Maike,
Mooi dat je dit zo aanbiedt.
Als docent rekenen op een mbo is dit artikel een handige opfrisbeurt.
WEL MAAK IK BIJ HET SCHEMA BREUKEN-PROCENTEN KOMMAGETALLEN OOK NOG EEN KOLOM MET DE TIENDELIGE BREUKEN, OPDAT DE STUDENTEN DE SAMENHANG DAN VOLLEDIG INZIEN.
DUS 1/4 25/100 0,25 25 %
Waarom doe ik dat. Immers op het mbo werken ze vaak met rekenmachientjes.
dus 37 % van 525 is dan 0,37 x 525
Groet,
Frits de Groot
Nimeto Utrecht
Beste Frits,
Fijn om te horen!
En dank voor je aanvulling.
Hartelijke groet,
Carola
zeer nuttige info om de kennis over te brengen naar kind
Bedankt voor je fijne en duidelijke uitleg
Super dit werkblad!!
Hier gaan we zeker mee aan de slag! Bedankt!
Heel erg bedankt! De schema is heel erg handig! Gr. Miki
Fijne, overzichtelijke informatie voor ons allemaal.
Thnx
Heel handig tks!
Een heel goed schema, plus wijze raad.
Dit moet in alle groepen 3 t.e.m. 18 (Univ.) opgehangen worden.
Hartelijk dank!!!
Wat fijn om zo iets overzichtelijk te hebben.
Misschien een leuke manier om dit te oefenen: ik heb zelf een memorie gemaakt met de breuken, procenten en kommagetallen. Uitgeprint, gelamineerd en uitgesneden. Ik weet niet of zoiets al bestaat, maar de kinderen vinden deze manier van oefenen erg leuk en de informatie wordt zo snel opgenomen.
Hi Liane, wat een goed idee! Dank je voor het delen.
Super en heel duidelijk uitgelegd. Zijn je zeer dankbaar.
Super, deze aandacht voor rekenen boeken en ook met name het schema voor breuken en procenten! Zelfs op het voortgezet onderwijs zal ze dit denk ik als ruggesteun gebruiken, want het is best lastig breuken en procenten en vooral ook
het oefenen met het LEZEN van de verhaalsommen , want dan pas kom je verder.
Het helpt ons als ouders ook enorm omdat je vaak moeilijk kunt uitleggen hoe dat werkt met breuken en procenten… op deze manier ontstaat er een aanleerstructuur!
Bedankt en vriendelijke groet,
S.Uyting.
Super handig dat schema! Sowieso een fijn steuntje in de rug wijzeroverdebasisschool.nl! Scholen gaan er vanuit dat de kinderen eigenlijk geen huiswerk hoeven te doen omdat de stof behandeld wordt in de klas. Het is toch een beetje wishful thinking, ben ik bang. Vind over het algemeen dat niet alles blijft hangen…Dus heel prettig dat deze info wordt aangeboden.
Hartelijke groeten,
Wilke Durand
Heel fijn dit!!! Super bedankt!!
Het schema hangt nu op de wc!
Goed idee. I.p.v. de tafelposter. Die is niet meer nodig.
Erg handig het schema.
Bedankt.
Hoi Maaike,
De schema is erg handig. Bedankt hier voor. Gr. Zouhra