Hoe bereken je procenten met een verhoudingstabel?

Procenten kom je overal tegen. In de winkel wanneer je korting krijgt, als je btw moet betalen, maar ook bij het downloaden van een bestand, bij rente, in krantenberichten en in reclameblaadjes.

Vanaf het rekenen in groep 7 krijgt je kind huiswerkopdrachten mee waarin bijvoorbeeld gevraagd wordt: hoeveel procent van de kinderen is brildragend? Of: hoeveel procent van de auto’s is rood?

Zo’n vraag is best een uitdaging, toch?

Meteen oefenen met procenten? Klik hier om de Spoedcursus Procenten te bekijken.

Beter scoren met procenten met de Nr.1 Formule

“Hoe je kind een 100% score haalt voor de moeilijkste sommen in groep 7 en 8 – binnen 2 weken“

Meer informatie

Bekijk ook:

• Procenten oefenen met de Nr. 1 formule
• Procenten berekenen, hoe doe je dat?
• Van breuken naar procenten en kommagetallen: een handig schema (PDF)
• Hoe bereken je een korting?

Rekenen met verhoudingen

Veel redactiesommen (verhaaltjessommen) zijn op te lossen met behulp van een verhoudingstabel. Hetzelfde geldt voor het berekenen van een percentage.

Een verhoudingstabel heeft rijen en kolommen. Een rij loopt van links naar rechts (horizontaal) en een kolom loopt van boven naar beneden (verticaal).

Een verhouding zegt niets over de grootte van de getallen, het zegt iets over de wijze waarop de getallen zich tot elkaar verhouden.

Je kunt een percentage op 2 verschillende manieren uitrekenen, zie voorbeeld 1A en 1B.

A. Door het totaal als 100% te zien.

B. Door de gegevens in de tabel onder elkaar te zetten.

Voorbeeld 1A

Er wonen 400 mensen in een flatgebouw, 80 van hen zijn kinderen. Hoeveel procent van de bewoners is kind?

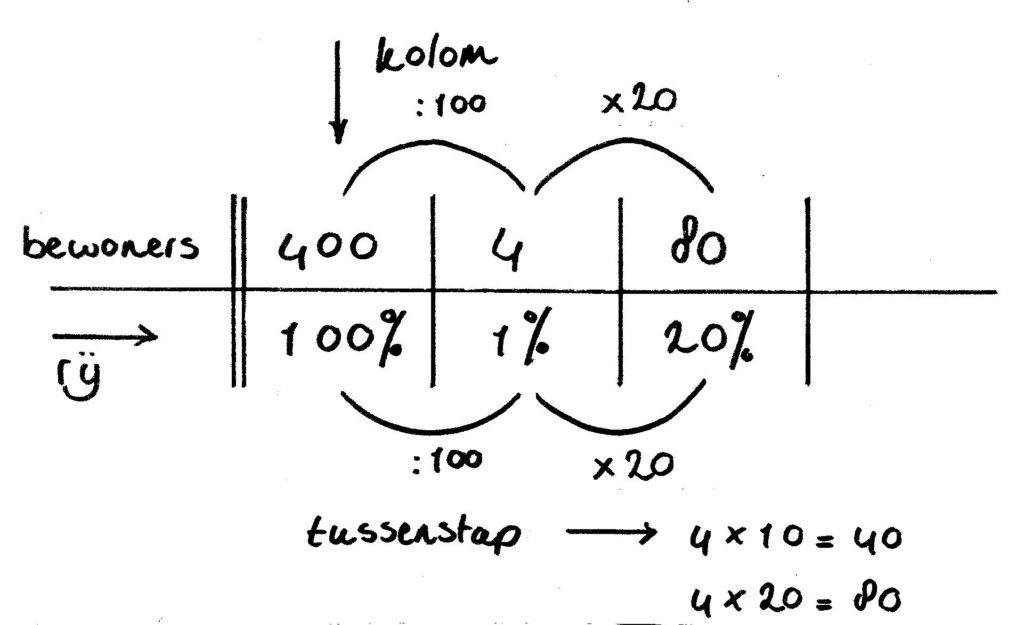
In de verhoudingstabel schrijf je deze gegevens (400, 100%, 1% en 80) als volgt op:

Je kunt in de som lezen dat 400 bewoners 100% is.

Reken nu eerst uit hoeveel 1% is.

Dat zijn 4 bewoners (400 : 100 = 4).

Hoeveel keer passen 4 bewoners in 80?

Dat is 20. Het antwoord is 20%.

Voorbeeld 1B

Er wonen 400 mensen in een flatgebouw. 80 van hen zijn kinderen. Hoeveel procent van de bewoners is kind?

In de verhoudingstabel schrijf je deze gegevens (80 van de 400) als volgt op:

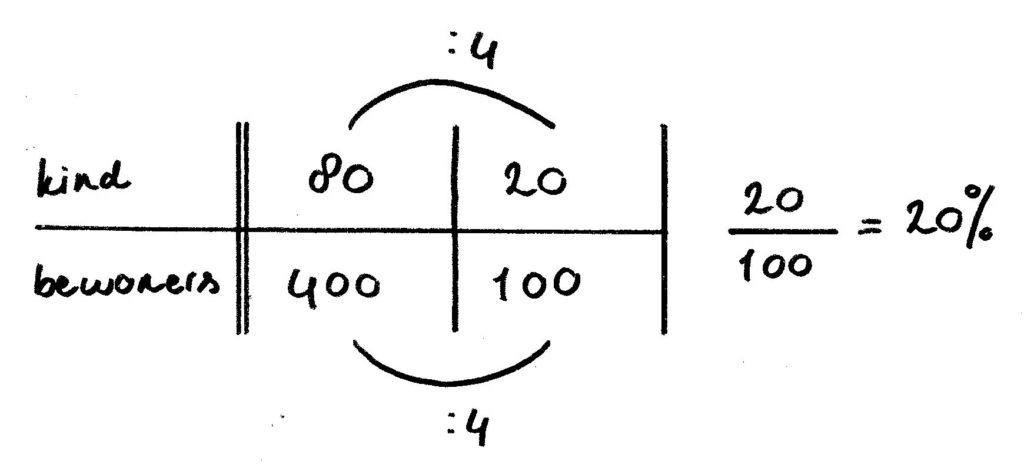
Je brengt 400 bewoners naar 100 bewoners.

Je deelt 400 door 4 om dat te bereiken. Dan deel je 80 kinderen ook door 4.

80 : 4 = 20. 20 van de 100 = 20/100 en 20/100 is 20%.

Het antwoord is 20%.

Verhoudingstabellen in groep 7

Wat moet je kind kunnen?

• Keertafels;
• Deeltafels;
• Inzicht hebben in de relatie tussen breuken en procenten;
• De instructie kennen: “Wat je boven de streep doet, doe je ook onder de streep” (deze instructie wordt verderop in dit artikel uitgelegd).

Keertafels

Als je kind de keertafels nog niet geautomatiseerd heeft (dat is wanneer het nog niet snel een antwoord weet op de verschillende keersommen), geef hem dan een tafelkaart met daarop de keertafels.

Het gaat nu om het leren van de strategie ‘rekenen met verhoudingstabellen’. Het is nodig dat je kind al zijn aandacht hierop kan richten, zonder dat het zich druk hoeft te maken over het antwoord op een tafelsom.

Deeltafels

Als je kind de deeltafels nog niet geautomatiseerd heeft (dat is wanneer het nog niet snel een antwoord weet op de verschillende deelsommen), geef hem dan een tafelkaart met daarop de deeltafels.

Het gaat nu om het leren van de strategie ‘rekenen met verhoudingstabellen’. Het is nodig dat je kind al zijn aandacht hierop kan richten, zonder dat het zich druk hoeft te maken over het antwoord op een tafelsom.

De relatie tussen breuken en procenten

Hieronder kun je een overzicht downloaden dat je kind uit zijn hoofd kan leren. Zo kan het deze kennis niet alleen bij verhoudingstabellen inzetten, maar ook tijdens de Cito-toetsen.

Alleen kennis van dit overzicht is natuurlijk niet voldoende. Het gaat erom dat je kind inzicht heeft in de relatie tussen breuken en procenten. Met procenten laat je zien hoe groot een bepaald deel is ten opzichte van het geheel.

Het geheel is 100%. Eén procent is 1/100 deel van het geheel. Het teken voor procent is %.

Vertel ook dat het woord ‘percentage’ hetzelfde betekent als ‘procent’ (per honderd).

Dat procent een deel is van een geheel, komt overeenkomt met breuken, ook zij zijn een deel van een geheel. Dit overzicht laat de onderlinge relatie zien:

 Hulp geven bij: percentage uitrekenen met een verhoudingstabel

Je kunt de instructie met je kind doornemen, bijvoorbeeld op onderstaande manier:

• Bereken zelf een aantal sommen en denk daarbij hardop na. Zo hoort je kind wat jouw denkstappen zijn (dat heet modeling). Wanneer je voor-denkt, helpt je je kind inzien hoe het een verhaaltjessom moet begrijpen en hoe het deze omzet in een kale som.
• Door visualisatie: je zet je denkstappen om in handelingen. Je laat nu letterlijk zien hoe je de som op papier uitrekent.
• Ook deze instructiefilm kan handig zijn:

• Daarna herhaal je bovenstaande punten en oefen je ze regelmatig. Net zo lang tot je kind een percentage kan berekenen met behulp van een verhoudingstabel.

Bereken percentage tussen twee getallen

Een voorbeeld:

Je wilt 10 euro sparen. Je hebt al negen euro. Hoeveel procent heb je al gespaard?

Manier A

Kijk welk gegeven (het aantal óf de procenten) je het makkelijkst kunt delen of vermenigvuldigen om te komen tot een antwoord op de vraag.

10 euro is 100%, 1 euro is 10%, dus 9 euro is 90%.

Manier B

Breng  het geheel naar 100.

In de verhoudingstabel schrijf je de gegevens als volgt op: 9 van de 10 = 90 van de 100 = 90/100 = 90%.

Sommige kinderen hebben baat bij het aanleren van (eerst) 1 strategie omdat ze anders de verschillende strategieën door elkaar halen.

Bespreek dit met je kind, zodat je weet bij welke leerstijl je kind zich het prettigst voelt.

Je oefent dan eerst 1 manier. Pas als deze manier goed ‘geborgd’ is, oefen je op de tweede manier.

Uiteindelijk wil je wel dat je kind beide manieren beheerst. Zo kan je kind altijd kiezen welke manier (A of B) hem het makkelijkst/snelst naar het antwoord op de som brengt.

Een voorbeeld:

In een winkel zijn 5 mensen. 4 mensen hebben een boodschappentas bij zich. Hoeveel procent van de mensen heeft een boodschappentas?

Nog een voorbeeld:

Je hebt 600 euro van de 800 gespaard. Hoeveel procent heb je dan al gespaard?

Nog een voorbeeld:

In een boekenwinkel zijn 3 boeken binnen een dag verkocht. Er zijn 20 boeken geleverd. Hoeveel procent is er verkocht?

Rekenen met verhoudingstabellen (hoeveelheid)

Als kinderen gaan rekenen met procenten, moeten ze twee dingen kunnen:

1. Het percentage kunnen berekenen zoals in voorgaande sommen is uitgelegd;
2. De hoeveelheid van een percentage uit kunnen rekenen.

De sommen waarbij de hoeveelheid van een percentage moet worden uitgerekend, ‘verkent’ je kind vanaf eind groep 6, waarna in groep 7 het serieuze werk begint 😉.

Een voorbeeld:

In een garage staan 25 auto’s. 12% van deze auto’s is rood. Hoeveel auto’s zijn rood?

Bij deze opdrachten kun je vertellen dat het makkelijk is om eerst 1% uit te rekenen.

Nog een voorbeeld:

Mohammed heeft 900 knikkers. Hij geeft 7% aan zijn vriend. Hoeveel knikkers krijgt de vriend van Mohammed?

Nog een voorbeeld:

Van een groep van 2600 kinderen kijkt 30% dagelijks tv. Hoeveel kinderen zijn dat?

Procenten en verhoudingen in groep 7 en 8

Zoals ik al eerder schreef: met een verhoudingstabel kun je veel sommen oplossen. In een verhoudingstabel zet je eerst de informatie die je uit de redactiesom kunt halen. De methode is om steeds de (twee) gegevens die je weet in de vakjes linksboven en linksonder te zetten en dan naar het antwoord toe te werken.

Korting = eraf (sommentaal)

Ongeveer = een schatting (sommentaal)

Een voorbeeld:

Een paar schoenen kost €120,-. In de winkel krijg je die dag 25% korting. Wat moet je betalen?

Omgekeerd kan de vraag ook gesteld worden.

Een voorbeeld:

Een fiets kostte eerst €60,-. Nu is het uitverkoop en betaal je nog maar €50,-. Hoeveel procent korting krijg je ongeveer?

Op deze afbeelding kun je zien dat je ook een aantal berekeningen bij elkaar kunt optellen maar…. Ook hier geldt: wat je beneden bij elkaar optelt, tel je ook boven bij elkaar op. Dit geldt natuurlijk ook voor het omgekeerde.

Een voorbeeld:

Op de afdeling waar je jassen kunt kopen, krijg je op alle jassen 60% korting. De jas die ik uitgekozen heb, kost nu €110,50. Wat was de prijs zonder korting?

De korting is 60%. Ik heb dus 40% betaald. €110,50 is dus 40%. Ik wil weten wat de prijs van de jas was zonder korting. Ik moet dus doorrekenen tot ik 100% kan uitrekenen.

Het volgende had ook gekund:

Eerst 20% uitrekenen en de uitkomst met 5 vermenigvuldigen.

€ 55,25 = 20% en € 55,25 x 5 = € 276,25

Nog een voorbeeld:

Een grote reep chocolade is afgeprijsd van €2,- naar €1,30. Hoeveel procent korting is dat?

Antwoord: de korting is €0,70 en ik wil weten hoeveel procent dat is van het bedrag voordat de korting eraf ging. De prijs van € 2,- is dus 100%.

Zie de afbeelding voor de uitwerking:

Hopelijk draagt bovenstaande uitleg bij aan meer plezier in rekenen 😊.

En als jouw uitleg niet in één keer wordt begrepen, bedenk dan dat je ook kunt zeggen:

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

Carola de Koning, BEd

Carola heeft ervaring opgedaan als bijlesjuf, kindercoach en als leerkracht in het basisonderwijs

Over Carola