HTE-rekenen met het HTE-schema

Is jouw kind wel eens thuisgekomen met afkortingen en rekenschema’s (zoals het HTE-schema) waarvan je niet direct wist wat ze betekenden? Tegenwoordig krijgen de kinderen op de basisschool op een andere manier rekenles dan je zelf waarschijnlijk kreeg. Alles draait om handige strategieën waarbij je vooral ook rekeninzicht nodig hebt. Als het rekeninzicht van je kind niet zo groot is, dan kunnen handige hulpmiddelen een uitkomst zijn. Zo kan je kind toch die complexe sommen met grote getallen uitrekenen.

In dit artikel bespreken we het HTE-schema. Wat is dit precies en hoe kun je het inzetten tijdens de rekenles? Het is handig als je dit weet, zodat je goed kunt aansluiten bij de manier waarop je kind het rekenen op school krijgt uitgelegd. Zo kun je je kind ook eenvoudig een handje helpen tijdens het maken van huiswerk.

HTE-schema uitleg

Het HTE-schema, wat is dat nu precies?

De letters HTE staan voor H = Honderdtallen, T = Tientallen en E = Eenheden.

Al vanaf groep 3 leren kinderen dat getallen verschillende waardes hebben. Een 2 is niet hetzelfde als 20 of 200. En het getal 38 bestaat uit 3 tientallen en 8 eenheden. In het getal 406 zitten 4 honderdtallen, 0 tientallen en 6 eenheden.

In het lokaal zie je daarom ook vaak een getallenlijn hangen. Soms van 0 tot 20, maar vaak ook van 0 tot 100. Door zo’n getallenlijn krijgt je kind inzicht in de positie van een getal. Je kind kan met zijn ogen de getallen volgen en herkennen dat een eenheid steeds wordt herhaald na het wisselen van een tiental. Begrijpen dat eenheden, tientallen en honderdtallen verschillende dingen zijn, is dus een belangrijke voorwaarde om te kunnen werken met het HTE-schema.

Maar hoe werkt dit schema nu precies?

Vanaf midden groep 5 leert je kind onder elkaar optellen en aftrekken. We noemen dit ook wel cijferend rekenen. Sommige scholen kiezen ervoor om dit eerder of later te doen. Dat hangt ook af van de rekenmethode die de school gebruikt.

Om het cijferend optellen en aftrekken handig uit te leggen, wordt vaak gebruik gemaakt van het HTE-schema. Met behulp van dit schema kun je vooral grote getallen handig uitrekenen.

HTE-schema plussommen

Laten we eens kijken naar een voorbeeld van een optelsom, waarbij gebruik wordt gemaakt van het HTE-schema.

We nemen deze som: 135 + 214 =

In bovenstaand schema zie je dat alle getallen precies onder elkaar staan, de eenheden, de tientallen en de honderdtallen. Dat is belangrijk! Als je je kind wilt helpen met het schema, is het dus belangrijk dat je dit duidelijk uitlegt. Het schema is daarom juist een handig hulpmiddel om de getallen op de juiste manier onder elkaar te zetten.

Vervolgens leer je je kind bij de eenheden te beginnen. Je zegt: “We beginnen bij de eenheden en rekenen uit hoeveel 5 + 4 is. Het antwoord schrijf je er precies onder, 9.”

Vervolgens ga je door naar de tientallen. Je zegt: “Nu gaan we naar de tientallen. Hoeveel is 3 + 1? Juist, het antwoord is 4, schrijf maar op.”

Tot slot ga je naar de honderdtallen en je zegt: “Als laatste gaan we naar de honderdtallen en reken je uit hoeveel 1 + 2 is. Het antwoord is 3, goed zo, schrijf maar op.”

Nu staat het antwoord van de som in het schema. Laat je kind het antwoord hardop zeggen, 349.

Bij dit voorbeeld zijn zowel de eenheden, de tientallen en de honderdtallen aan bod gekomen.

Om een stapje verder te gaan, nemen we een wat complexere som: 49 + 23 =

Bij deze som begin je ook weer bij de eenheden. Dus: 9 + 3 = 12. Die 12 past niet helemaal in de kolom van de eenheden. Het is belangrijk dat je je kind leert om alleen de 2 van 12 op te schrijven. Dat is namelijk de eenheid in het getal 12. De 1 van het tiental moet je kind als geheugensteuntje boven de 4 schrijven.

Dan ga je naar de tientallen. Er staat nu 1 + 4 + 2. Benadruk dat dit de tientallen zijn en dat er dus eigenlijk staat: 10 + 40 + 20. Het antwoord is 7 (eigenlijk dus 70). Je schrijft de 7 op. Nu staat er 72. Laat je kind het antwoord ook weer hardop zeggen. Dan hoort je kind dat de 2 een 2 is en de 7 het getal 70 is.

Het gaat er dus vooral om dat je kind begrijpt wat het aan het doen is. Door samen hardop te benoemen wat je doet en wat de getallen betekenen, leer je je kind dit op de juiste manier te doen.

Oefenbladen Klokkijken Groep 4/5 (Gratis)

Download

Oefenbladen Rekenen Groep 5 (Gratis)

Download

HTE-schema minsommen

Bij de minsommen gaat het met de eenvoudige sommen eigenlijk precies zo. Het wordt wat ingewikkelder als er geleend moet worden bij de getallen. Maar laten we eerst een eenvoudige minsom uitrekenen met behulp van het HTEschema.

We nemen deze som: 79 – 45 =

Net als bij de plussommen begin je ook hier weer bij de eenheden. Je zegt: “Hoeveel is 9 – 5?” Het antwoord, 4, schrijf je onderaan in dezelfde kolom. Dan ga je naar de tientallen. Je zegt: “Nu de tientallen. Hoeveel is 7 – 4? Goed zo, dat is 3. Welk getal staat er nu? Juist, 34.”

Het wordt wat ingewikkelder bij het volgende voorbeeld: 32 – 15 =

Ook hier begin je weer bij de eenheden. Je zegt: “Hoeveel is 2 – 5? Oh jee, dat kan niet! Nu moeten we gaan lenen bij de buren, de tientallen, want die hebben nog genoeg! We lenen 1 tiental, dus 10. En die doen we bij de 2. Nu hebben we dus het getal 12!”

Maak hier dus duidelijk dat er een tiental wordt geleend en bij de eenheid wordt opgeteld. “Hé, nu kunnen we weer verder, want 12 – 5 kunnen we wel uitrekenen. Hoeveel is dat? Juist, 7! Schrijf de maar 7 op.”

Nu ga je door naar de tientallen. Van het getal 3 heb je een tiental geleend, dus zijn er nog 2 over. De som wordt nu 2 – 1 = 1. Je schrijft de 1 op. “Welk antwoord staat er nu? Juist, 17.”

We zullen ook nog een voorbeeld geven met honderdtallen waarbij geleend moet worden.

We nemen deze som: 425 – 247 =

Begin weer bij de eenheden zoals altijd en zeg: “Hoeveel is 5 – 7? Oh, we zien het al, dat kan niet, dus we gaan weer lenen bij de buren.” Van het tiental 2 leen je weer 1 tiental, waardoor het getal 5 nu 15 wordt. “Nu kunnen we wel aftrekken, namelijk 15 – 7 = 8. Schrijf de 8 maar op.”

Vervolgens ga je naar het tiental. Er is al een tiental van de 20 af, dus blijft er nog 1 over, oftewel 10. Je zegt: “Hoeveel is 1 – 4? Oh jee, dit kan ook niet, we moeten weer naar de buren!” Vervolgens ga je naar het honderdtal en leent daar 1 honderdtal. De 1 (10) wordt nu 11 (110) en de som wordt 11 – 4 = 7 (110 – 40 = 70). Schrijf de 7 op.

Ten slotte ga je nog naar de honderdtallen. Van de 4 is al een honderdtal geleend, dus daar blijven er nog 3 (300) over. De som wordt 3 – 2 = 1 (300 – 200 = 100). Schrijf op 1. Het antwoord op de som is 178.

Zorg ervoor dat je als ouder een paar keer hardop voordoet wat je doet. Denk dus hardop en laat je kind meeluisteren. Door het goede voorbeeld te geven, volgt je kind en zal hij makkelijker jouw instructie overnemen.

Oefen dit een paar keer achter elkaar tot je kind het zelf kan. Benadruk steeds dat het hier om eenheden, tientallen en honderdtallen gaat, maar dat je dus met hulp van dit HTE-schema de som makkelijker kan uitrekenen door de getallen te lenen en klein te houden.

HTE-schema werkblad leeg

Om je kind te helpen is het handig om een voorbeeld in een leeg schema te zetten. Zo kan je kind steeds weer even teruggrijpen naar het voorbeeld. Ook kun je het lege HTE-schema gebruiken om je kind te laten oefenen met zowel plus- als minsommen. Als je het lege werkschema print, kun je het daarna plastificeren. Met een whiteboardstift kun je dan het schema steeds weer opnieuw invullen en weer schoonvegen.

DHTE-schema

Als je kind eenmaal het HTE-schema begrijpt, zal de overstap naar het DHTE-schema niet meer zo groot zijn. Hierbij gaat je kind ook duizendtallen toevoegen.

Laten we even kijken naar deze voorbeeldsom: 934 + 315 =

Begin ook nu bij de eenheden: 4 + 5 = 9. Schrijf de 9 op. Vervolgens ga je naar de tientallen: 3 + 1 = 4. Schrijf de 4 op. Dan naar de honderdtallen: 9 + 3 = 12. Maak hierbij duidelijk dat je dus eigenlijk 900 en 300 bij elkaar optelt en dat dat 1200 is. Dat betekent 2 honderdtallen (200) en 1 duizendtal (1000). Merk op dat er nu dus een duizendtal bij is gekomen. Je schrijft de 2 van de honderdtallen direct onder de honderdtallen en de 1 van de duizendtallen schrijf je er links naast, onder de D van duizendtallen. Er is nu dus 1 duizendtal bij gekomen.

Meerdere getallen bij elkaar optellen

Tot nu toe hebben we steeds 2 getallen bij elkaar opgeteld, maar je kunt natuurlijk ook meerdere getallen bij elkaar optellen.

Bijvoorbeeld 3362 + 868 + 13 + 8 =

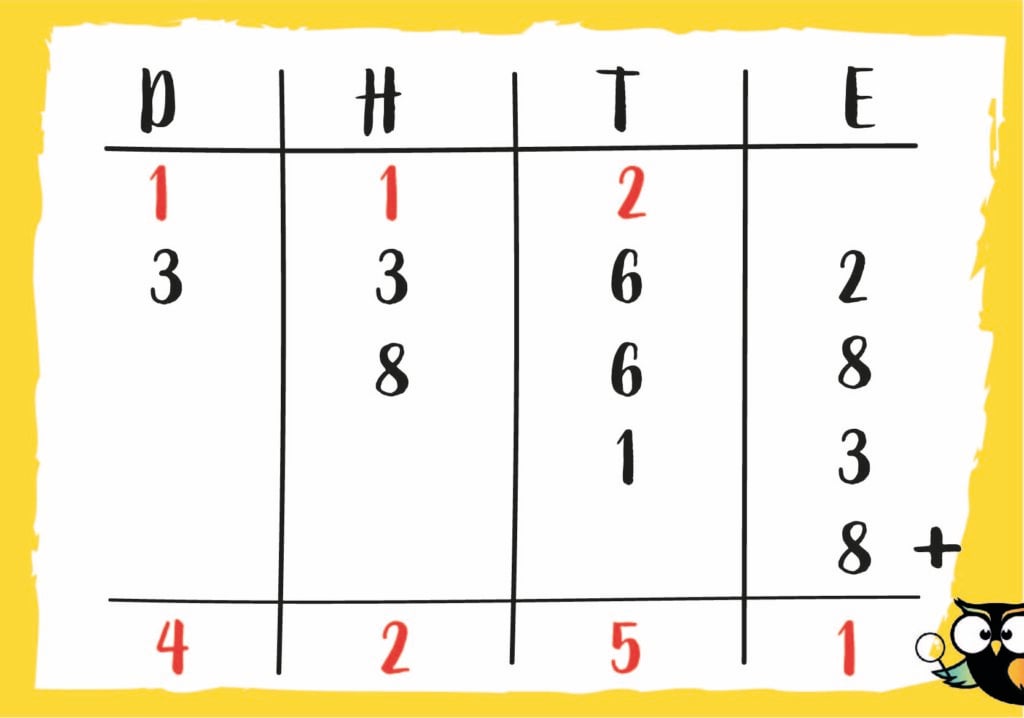
Laat je kind deze getallen eerst goed onder elkaar zetten en benoem wat de waarde van elk cijfer is. Is het een duizendtal, een honderdtal, een tiental of een eenheid?

Vervolgens ga je de getallen optellen en begin je uiteraard weer bij de eenheden. Je zegt: “2 + 8 + 3 + 8 = 21. Ik schrijf de 1 op, want dat zijn de eenheden. De 2 schrijf ik boven de tientallen.”

Dan ga je naar de tientallen. Je zegt: “6 + 6 + 1 + de 2 die erbij zijn gekomen, maakt samen 15.” Schrijf de 5 op in de kolom van de tientallen. De 1 schrijf je boven de honderdtallen.

Dan ga je door naar de honderdtallen en zegt: “3 + 8 + de 1 die erbij is gekomen is, maakt samen 12”. Schrijf de 2 op in de kolom van de honderdtallen. De 1 schrijf je bovenaan de kolom van de duizendtallen.

Tot slot ga je naar de duizendtallen. In dit geval gaat het alleen om de 3 + de 1 die erbij is gekomen. 3 + 1 = 4. Je schrijft de 4 op. 

Blijf iedere stap hardop benoemen, zodat je kind jouw gedachten kan volgen.

Uiteraard kun je het schema nog meer uitbreiden met tienduizendtallen, honderdduizendtallen en miljoenen. Het principe van het optellen en het aftrekken blijft steeds hetzelfde. Als je kind eenmaal door heeft hoe het werkt, dan zul je merken dat de grootste sommen geen enkel probleem meer zijn. Ook je kind zal wellicht verbaasd zijn hoe goed hij nu grote getallen kan uitrekenen!

Bekijk ook deze andere onderwerpen:

Marja Wouda, BEd Master SEN

Marja (MSEN) is Remedial Teacher, Intern Begeleider, Kindercoach en behaalde een Bachelor of Education (PABO) en een Master SEN.

Over Marja