Redactiesommen groep 7

- Redactiesommen groep 7: video
- Kun je redactiesommen tekenen?
- Voorbeelden van verhaaltjessommen in groep 7
- Een schema voor redactiesommen groep 7 maken
- Een truc voor redactiesommen in groep 7 met grote getallen erin
- Verhaaltjessommen met breuken
- Rekentaal in groep 7: belangrijke tip!
- Nog wat voorbeelden
- Verhaaltjessommen met verhoudingen in groep 7
- Verhaaltjessommen in groep 7 met schaal berekenen
- Afronden groep 7 in de vorm van een verhaalsom
- Verhaalsommen met tijd in groep 7
- Redactiesommen groep 7 oefenen en meer tips

Veel kinderen in groep 7 vinden verhaaltjessommen moeilijk. Een zogenaamde ‘kale som’ is vaak in een heel andere vorm verstopt in een verhaaltje. De volgende tips helpen je kind echt redactiesommen groep 7 op te lossen.
Om verhaaltjessommen goed op te kunnen lossen, is het belangrijk om de taal die wordt gebruikt in deze sommen te begrijpen. De onderstaande video bevat een belangrijke tip over redactiesommen groep 7 met breuken.
Wil je met redactiesommen oefenen? Dan kun je het oefenboek groep 7 – 1e helft schooljaar bestellen. Dit boek is afgestemd op de Cito-toets rekenen groep 7 in januari.
Redactiesommen groep 7: video
Zoals je in de video hebt kunnen zien, is het belangrijk om te checken of je kind bepaalde uitdrukkingen die vaak in verhaaltjessommen worden gebruikt, goed kent. Je kunt je voorstellen dat er veel onnodige fouten worden gemaakt als dit niet het geval is.
Op deze website staan al een paar artikelen over verhaalsommen: een uitgebreid algemeen artikel waarin 4 verschillende strategieën worden besproken en 2 artikelen die specifiek over verhaalsommen in groep 6 en 8 gaan.
Dit artikel gaat over verhaalsommen die bij rekenen in groep 7 voorkomen.
Groep 7 wordt vaak de moeilijkste groep genoemd. Dat komt omdat alle leerstof dit jaar wat abstracter wordt. Bij taal wordt er een groot deel van het ontleden en de werkwoordspelling toegevoegd aan de leerstof. Bij rekenen komen de (kale) breuken, de procenten en de lastigere kommagetallen erbij. Verder worden de getallen steeds groter. Je kind werkt dit jaar met getallen tot 1 miljoen. Inzicht wordt steeds belangrijker.
Kun je redactiesommen tekenen?
Om verhaalsommen in groep 7 op te lossen, kun je verschillende strategieën gebruiken. Als je kind moeite heeft met begrijpend lezen, is de kans groot dat het ook moeite heeft met verhaalsommen. In beide gevallen gaat het er namelijk om dat je hoofdzaken en bijzaken kunt scheiden.
Juist omdat de stof steeds abstracter wordt, is het goed om in dat geval bij verhaalsommen de opgave te tekenen. Door het tekenen wordt het weer wat minder abstract.
Je kunt natuurlijk letterlijk een tekening maken bij het verhaal in de som. Voor sommige kinderen is dat een noodzakelijke eerste stap. Maar je zult merken dat je kind er gauw genoeg van krijgt. Bijvoorbeeld als het 24 kinderen moet tekenen. Je kind zal dan zelf bijvoorbeeld een rondje of kruisje gaan neerzetten voor ieder kind. Vanuit zo’n schema kan het dan verder gaan denken over de oplossing van de som.
Een volgende keer zal je kind direct een schematischere tekening maken. Heeft het bij een bepaald soort som al vaak een schematische tekening gemaakt, dan zul je zien dat het niet meer nodig is om het schema op papier te zetten. Het is dan al voldoende om eraan te denken.
Als je kind vaak genoeg oefent met het schematiseren van verhaalsommen, zul je overigens zien dat het ook effect heeft op het begrijpend lezen.
Voorbeelden van verhaaltjessommen in groep 7
Een paar voorbeelden van verhaalsommen met stappenplan en bijbehorend schematiseringen:
Paul en zijn kleine broertje Simon ontbijten samen. Ze eten brood met pindakaas en hagelslag. Paul snijdt de boterhammen van Simon in 4 stukken. Van zijn laatste boterham eet Simon maar 2 stukken. De rest eet Paul nog op. Paul heeft dan 3 keer zoveel gegeten als Simon. Samen hebben ze 10 boterhammen op. Hoeveel heeft Simon gegeten?
Stap 1: lees het verhaaltje 2 keer goed en probeer het voor je te zien.
Stap 2: Lees de vraag. Welke informatie gebruik je om de vraag te beantwoorden?
Antwoord: Dat Paul 3 keer zoveel eet als Simon en dat ze samen 10 boterhammen hebben gegeten.
Stap 3: teken het verhaal: Als Paul 3 boterhammen heeft gegeten, heeft Simon er 1 op.
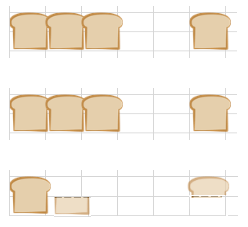
Simon heeft 2,5 boterham gegeten en Paul 7,5. Dat is 3 keer zoveel.
Door in deze opgave de vraag te stellen: welke informatie heb je nodig om de vraag te beantwoorden, wordt gelijk duidelijk welke informatie overbodig is. Maar dan nog is het lastig om de vraag te beantwoorden.
Door de som gewoon te gaan tekenen, wordt gaandeweg ook duidelijk hoe hij opgelost kan worden. Als je kind meer van dit soort opgaven gaat maken, zal het steeds makkelijker gaan schematiseren. Zeker als de getallen groter worden. Een simpel kruisje per voorwerp is de volgende stap. Daarna zal je kind gewoon de getallen opschrijven.
Een schema voor redactiesommen groep 7 maken
Een nog handigere manier om dit soort sommen op te lossen zal je kind misschien niet zo snel bedenken. Toch bestaat hij en het is zeker een aanrader om ermee te oefenen. Dit is het schema bij deze som:

Hier is gelijk duidelijk dat je die 10 boterhammen in 4 gelijke porties moet verdelen. 10 : 4 = 2,5. Simon krijgt er dan 2,5 en Paul 3 x 2,5 = 7,5.
Een truc voor redactiesommen in groep 7 met grote getallen erin
Als er grote of lastige getallen in een opgave staan, worden veel kinderen onzeker. Ze zien dan vaak niet meer hoe ze de opgave moeten oplossen. Als ze dan de lastige getallen even vervangen door makkelijke getallen, zien ze vaak de oplossing wel.
Anja krijgt 70% korting op een bank. Ze moet nu nog € 990 betalen. Hoeveel kostte de bank eerst?
Het is best lastig om te zien hoe deze som uitgerekend moet worden. Vul daarom eerst makkelijkere getallen in:
Anja krijgt 25% korting op een bank. Ze moet nu nog € 750 betalen. Hoe duur was de bank eerst?
Misschien ziet je kind het antwoord nu gelijk. Laat het dan toch even nadenken hoe hij de som zou kunnen uitrekenen:
€ 750 is dus 75% (100% – 25%). 25% is dus € 250. De bank kostte eerst 25% + 75% dus 750 + 250 = 1000 euro.
Met de moeilijker getallen gaat het dus hetzelfde:
€ 990 = 30% (100% – 70%). Nu moet je nog weten hoeveel 70% dan is, en dat dan optellen bij die € 990.
30% = € 990 dus 10% = € 330. 70% is dus 7 x € 330 = € 2310. De bank kostte eerst 30% + 70% = € 990 + € 2310 = € 3300.
Verhaaltjessommen met breuken
We kijken eerst naar de volgende kale som:
¼ van 96 = 24
Deze som is vaak opgenomen in een verhaaltjessom in de Cito-toets of in de rekenmethode. In het verhaaltje wordt de breuk soms zelfs niet als breuk opgenomen. Ik geef hieronder een voorbeeld van een redactiesom uit groep 7. De voorbeeldsommen komen uit het oefenboek rekenen groep 7- 2e helft schooljaar van ‘Aandacht voor rekenen’.
1 van de 4 kinderen van turnclub WIK is ouder dan 10 jaar. Er zitten 96 kinderen op turnclub WIK. Hoeveel kinderen zijn ouder dan 10 jaar?
……………. kinderen
Dit is exact dezelfde som als de bovenstaande kale som. De som wordt helaas vaak niet door kinderen herkend. Wat kun je hier zelf als ouder aan doen?
Rekentaal in groep 7: belangrijke tip!
Controleer of je kind de betekenis van bijvoorbeeld ‘1 van de 4’ of ‘1 op de 4’ goed weet. Dit is namelijk hetzelfde als ¼. Als je kind dit niet goed weet, herhaal dit dan een aantal keer.
Vervolgens is het nuttig om hiermee te oefenen. Begin dan met de kale sommen en laat je kind daarna redactiesommen maken. Je kind gaat de sommen dan goed herkennen.
Een aantal voorbeelden:
- Op een school zitten 144 kinderen. Eén vierde deel daarvan wordt met de auto gebracht. Hoeveel kinderen zijn dat?
- Een koopman koopt 364 appels in. 1 op de 4 appels is niet goed meer. De rest verkoopt hij voor 0,35 per stuk. Hoeveel zijn dat er?
- Van de 928 bomen in het bos is 25% een eik. Hoeveel zijn dat er?
- De oppervlakte van Peters tuin is 164 m2. Hij wil een kwart van zijn tuin betegelen. Hoeveel m2 is dat?
In al deze verhaalsommen moet je het geheel delen door 4.
- Eén van de 4 kinderen in de klas bespeelt een instrument. Dat zijn 6 kinderen. Hoeveel kinderen zitten er in de klas?
Hier is de som omgedraaid: ¼ = 6. Het geheel is dus 4 keer zoveel: 24.
Je kind moet verder begrijpen dat:
0,25 van 64 = 0,25 x 64
0,25 = ¼, dus dat is weer hetzelfde als ¼ van 64, oftewel ¼ x 64
In alle gevallen reken je de som uit door 64 te delen door 4.
In het oefenboek rekenen groep 7 – 2e helft schooljaar van ‘Aandacht voor rekenen’ zijn op pagina 85 t/m 104 sommen over breuken en procenten opgenomen. Hier staan ook veel verhaaltjessommen bij.
Verbanden tussen breuken, procenten en kommagetallen
In verhaalsommen wordt ook naar verbanden tussen de breuken, kommagetallen en procenten gevraagd:
In een bos staan 815 bomen. 3 van de 5 bomen zijn eiken. Hoeveel procent is dat?
Om deze som op te lossen moet je kind de volgende kennis gebruiken:
3 op de 5 is hetzelfde als 3/5.
1/5 = 20%.
3/5 is dus 3 x 20% = 60%.
Je kind moet ook weten dat een deling ook altijd als een breuk geschreven kan worden:
5 : 7 = 5/7 en 3 : 8 = 3/8.
Het deelteken kun je dus ook schrijven als een breukstreep. Dat is handig bij een som als deze:
6 kinderen verdelen 8 repen. Welk deel krijgt ieder?
Uitleg: als het 2 kinderen zouden zijn die 4 repen verdelen, zou de som 4 : 2 = 2 zijn. Bij deze som kun je dus ook gewoon 8 : 6 uitrekenen. Die deling kun je ook schrijven als 8/6 = 1 2/6 = 1 1/3. Dat is dus ook gelijk het antwoord.
In mijn ervaring is deze kennis bij lang niet alle kinderen geautomatiseerd. Doe er dus je voordeel mee en oefen regelmatig.
Nog wat voorbeelden
Andere verhaalsommen met breuken:
Hannah en Frank willen hun hele tuin betegelen. Hannah heeft 1/3 deel van de tuin betegeld en Frank heeft 2/5 deel gedaan. Welk deel moet nu nog betegeld worden?
Om deze opgave op te lossen, moet je kind weten dat 1/3 hetzelfde is als 5/15. En dat 2/5 net zoveel is als 6/15. Samen hebben ze dus 5/15 + 6/15 = 11/15 betegeld. Er moet dus nog 4/15 gedaan worden.
Heeft je kind moeite met dit soort opgaven, lees dan een uitgebreide uitleg in dit artikel:
Verhaaltjessommen met verhoudingen in groep 7
Een opgave die op bovenstaande opgaven lijkt is de volgende:
Voor 1 glas limonade heb ik 0,2 dl siroop nodig. Hoeveel glazen limonade kan ik inschenken als ik 3½ liter siroop heb?
Deze opgave kan op verschillende manieren opgelost worden, maar in ieder geval moet je kind weten hoeveel keer 0,2 dl in een dl gaan (5) en hoeveel dl er in een liter zitten (10). Daarna kan je kind de opgave oplossen door hem te tekenen: 5 glazen per dl, dus 5 x 10 per liter = 50 glazen. Met 3,5 liter kan je dus 3,5 x 50 glazen maken = 175 glazen.
Een andere oplossingmethode is de verhoudingstabel. Een verhoudingstabel is een overzichtelijke manier om sommen met verhoudingen op te lossen. In dit geval is de verhouding 0,2 dl per glas.

Zoals je ziet doe je in een verhoudingstabel boven en onder hetzelfde. Ingewikkelde opgaven worden op deze manier een stuk simpeler.
Het centrale woord bij deze opgave is het magische woordje ‘per‘. Als dat woordje in een opgave staat of erin gezet kan worden, kun je de som oplossen met een verhoudingstabel.
In bovenstaande opgave staat het woord niet, maar je zou hem kunnen herschrijven: je hebt 0,2 dl per glas nodig. Hoeveel glazen haal je dan uit 3,5 liter siroop?
Andere opgaven die zo opgelost kunnen worden zijn bijvoorbeeld opgaven met km per uur en € .. per kilo.
In het artikel over verhaalsommen in groep 8 worden nog veel meer voorbeelden gegeven van opgaven die opgelost kunnen worden met de verhoudingstabel. Daar staan ook voorbeelden van sommen met procenten. Procent betekent namelijk letterlijk: per 100. 35% is dus 35 per 100. Net zoals je 1 per 4 kunt schrijven als ¼, kun je 35 per 100 dus schrijven als 35/100. Zet de deelstreep horizontaal en je hebt weer het begin van een verhoudingstabel. En zo hangen al deze getallen met elkaar samen.
Verhaaltjessommen in groep 7 met schaal berekenen
Ook schaalsommen komen in groep 7 aan de orde. Voor deze sommen is een verhoudingstabel ook handig.
Een voorbeeld:
Mijn tuinpad is 2,50 m lang. Ik teken mijn tuin op een schaal van 1:50. Hoeveel cm wordt mijn tuinpad op de tekening?
1:50 (1 op 50) betekent dat 1 cm op papier in het echt 50 cm is. Het pad is in het echt 2,5 m. Dit getal moet eerst omgerekend worden naar cm (250). Vervolgens kun je het invullen in de tabel en zie je al snel dat het antwoord 5 cm moet zijn.
Leer je kind om schaalsommen altijd met een verhoudingstabel uit te rekenen.

Afronden groep 7 in de vorm van een verhaalsom
Je kind gaat ook verhaalsommen krijgen waarin afgerond moet worden. Een voorbeeld:
In Verwegistan wonen 3.567.870 mensen en in Nogverderland wonen er 6.345.770. Bij elkaar is dat ongeveer
a. 9 miljoen c. 9,9 miljoen
b. 9,8 miljoen d. 10.000.000 miljoen
Om deze opgave op te lossen, moeten de getallen eerst afgerond worden. Antwoord a kan het niet zijn: als je afrondt op hele miljoenen, moet je kijken naar het getal achter de hele miljoenen.
3.567.870: bij 5 of hoger rond je naar boven af. De 3 wordt dus een 4, dus dit getal kan worden afgerond op 4.000.000, oftewel 4 miljoen.
6.345.770: de 3 is lager dan 5, dus rond je naar beneden af: 6 miljoen.
Bij elkaar dus 10 miljoen. En dus geen 10.000.000 miljoen zoals antwoord d. Het woord ‘miljoen’ vervangt namelijk de 6 nullen.
Dan blijven er 2 antwoorden over die op de 100.000 zijn afgerond. Om te weten welke van de 2 het goede antwoord is, kijk je naar het getal achter het honderdduizendtal:
3.567.870. 6 is hoger dan 5, dus het getal wordt naar boven afgerond: 3.600.000 oftewel 3,6 miljoen.
6.345.770: 4 is lager dan 5 dus rond je af naar beneden: 6.300.000 oftewel 6,3 miljoen.
Bij elkaar wordt het dus 3,6 miljoen + 6,3 miljoenen = 9,9 miljoen. Antwoord c dus.
Verhaalsommen met tijd in groep 7
Je kind moet op de minuut kunnen uitrekenen hoelang bijvoorbeeld een treinreis duurt, of tot op de honderdste seconde hoeveel tijd er zit tussen de finish van schaatsers. Maar ook hoeveel dagen er zitten tussen 2 data in opeenvolgende jaren.
Chantal is geboren op 10-01-2010. Op 25 juni 2017 wil ze weten hoeveel dagen het nog duurt voordat ze 8 wordt. Hoeveel dagen zijn dat?
Je kind heeft hier nogal wat basiskennis voor nodig. Het moet weten:
- dat 10-1 hetzelfde is als 10 januari;
- welke maanden er tussen juni en januari zitten;
- hoeveel dagen er in die maanden zitten.
Om het overzicht te houden, is het handig om ook hier weer een schema bij te maken:

Redactiesommen groep 7 oefenen en meer tips
Zoals je in de video hebt kunnen zien, is het belangrijk om te checken of je kind bepaalde uitdrukkingen die vaak in verhaaltjessommen worden gebruikt, goed kent. Je kunt je voorstellen dat er veel onnodige fouten worden gemaakt als dit niet het geval is. Wil je thuis oefenen met verhaaltjessommen voor groep 7? Bekijk dan de oefenboeken rekenen groep 7.
Nog meer tips voor groep 7:
Oefenbladen Cito/IEP-toets Groep 7 (Gratis)
Oefenbladen Rekenen Groep 7 (Gratis)
- Redactiesommen groep 3
- Redactiesommen groep 4
- Redactiesommen groep 5
- Redactiesommen groep 6
- Redactiesommen groep 8









Door G. Van Werven ,mijn dochter Gerlinde zit in groep 7 ,u heeft het goed uit gelegd met de breuken bedankt.
Hallo kunt u mij helpen met deze redactiesom te berekenen of uit te leggen. Een aquarium is 6 dm lang en 40 cm breed. Het water moet 20 cm hoger komen te staan. Hoeveel liter water moet erbij? Ik weet deze som zelf niet uit te leggen aan mijn dochter van 10. Kunt u mij helpen?
Beste C,
In deze som wordt gevraagd naar de inhoud: het aquarium is 6 dm lang, 4 dm breed en 2 dm hoog. De som wordt 6 x 4 x 2 = 48 dm3. 48 dm3 is hetzelfde als 48 liter.
Meer uitleg over het onderwerp meten vind je hier: https://wijzeroverdebasisschool.nl/uitleg/meten
Succes!
Hartelijke groet,
Carola
mijn dochter van 10 heeft op de redactiesom 6. Op de weegschaal staat 1.356 kg. Hoeveel gram is dit ? 1356 gram als antwoord, dit wordt fout gerekend en moet 13.560 zijn volgens de juf ?! Zelf denk ik dat er weinig weegschalen zijn die 1356 kilo aankunnen en het eerste antwoord toch juister is..
Dat lijkt mij ook Henk. Er zou een komma moeten staan waar een punt staat, denk ik… Hartelijke groet, Maaike
Hartelijk dank voor alle nuttige informatie en tips.
Onze dochter krijgt zo meer zelfvertrouwen.
Bedankt voor de heldere uitleg en de reken tips. Onze kleinkinderen hebben er veel baat bij.
Beste Wil,
Dank voor de reactie en veel succes met het oefenen van de redactiesommen.
Hartelijke groet, Maaike
Het is prima.
Met een drukke bijlespraktijk thuis kan ik het volgende melden.
De door Maaike uitgegeven boeken munten uit door hun eenduidige uitleg en heldere leerstof.
Mijn complimenten.
De slogan “Eerst de kale som leren en dan pas redactiesommen”, onderschrijf ik van harte.
Wij vinden prof. Jan van de Craats aan onze zijde. Zie zijn vele publicaties op rekengebied. (https://nl.wikipedia.org/wiki/Jan_van_de_Craats)
Een aanvullend tip mijnerzijds is deze: Let op de manier waarop kinderen de berekeningen van redactiesommen opschrijven. (Kinderen MOETEN van mij altijd de berekening leveren.)
B.v. deze som:
Ik heb een zakje met 14 knikkers, eentje met 7 knikkers en eentje met 24 knikkers.
Drie kinderen delen alle knikkers met elkaar. Hoeveel knikkers krijgt ieder kind?
Leerlingen schrijven dan vaak:
14 + 7 + 24 = 45 : 3 = 15
Deze berekening reken ik NIET goed. Hier staan twee sommen achter elkaar die niet “gelijk” zijn.
Het teken ” = ” betekent “is gelijk aan”.
Hier is 14 + 7 + 24 NIET gelijk aan 45 : 3
Hoe dan wel opschrijven?
Zo dus:
14 + 7 + 24 = 45
45 : 3 = 15
Peter de Visser
Beste Peter,
Dank je voor de nuttige aanvulling!
wel zo toch—-> (14+7+24):3=45:3=15
f.e. (23/10/2018)Zeer zeker, maar deze vorm van noteren eist óók nog goed inzicht in “volgorde van bewerkingen” bij de leerling.
Ik vind de informatie goed die ik per mail krijg en mijn dochter leer er veel van.
Ik bedank jullie ook hiervoor