
Een verhouding laat zien hoe twee getallen zich tot elkaar verhouden. Een verhouding zegt niets over de grootte van de getallen. In dit artikel leggen we uit hoe je met een verhoudingstabel kunt werken. Handig om te gebruiken bij het uitrekenen van procenten.
Een voorbeeld:
Peter fietst 2 keer sneller dan Teun. We weten niet hoe hard beide mannen dan fietsen. We weten alleen dat Peter 2 keer sneller fietst dan Teun. Het zegt iets over de verhouding tussen de snelheden die Peter en Teun fietsen.

- Als Teun 10 kilometer per uur fietst, dan fietst Peter 20 kilometer per uur.
- Als Teun 12,5 kilometer per uur fietst, dan fietst Peter 25 kilometer per uur.
De snelheid van Teun verhoudt zich tot de snelheid van Peter als 1 : 2. Dit spreek je uit als: één staat tot twee.
Als Teun 17 kilometer per uur fietst, dan fietst Peter twee keer zo snel, dus 2 x 17 = 34 kilometer per uur.
Nu andersom: als Peter 40 kilometer per uur fietst, dan fietst Teun de helft van de snelheid van Peter: 40 : 2 = 20 kilometer per uur.

Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 6 (Gratis)

Oefenbladen Rekenen Groep 7 (Gratis)
Verhoudingstabel
Een mooi middel dat je kunt gebruiken bij het rekenen met verhoudingen (en bij bijna alle rekenopgaven) is de verhoudingstabel.
Bovenstaand voorbeeld ziet er in een verhoudingstabel als volgt uit:

Nog een voorbeeld:
Het gewicht van een kleine en een grote loden kogel verhoudt zich als 1 : 3. We weten niet hoe zwaar beide kogels zijn. We weten alleen dat de grote kogel 3 keer zwaarder is dan de kleine kogel.
- Als de kleine kogel 500 gram weegt, dan weegt de grote kogel 1500 gram (of 1,5 kilogram).
- Als de kleine kogel 1 kilogram weegt, dan weegt de grote kogel 3 kilogram.
- Als de kleine kogel 130 centigram weegt, dan weegt de grote kogel 3 x 130 = 390 centigram.
- Als de grote kogel 1200 hectogram weegt, dan weegt de kleine kogel 1200 : 3 = 400 hectogram.
Terug naar ons eerste voorbeeld.
Teun traint hard en gaat sneller fietsen. Na twee maanden is de verhouding tussen de snelheden die Teun en Peter fietsen 2 : 3 (spreek uit als twee staat tot drie).
Als Teun 12 kilometer per uur fietst, hoeveel kilometer per uur fietst Peter dan?
Laten we dit eens in een verhoudingstabel zetten:
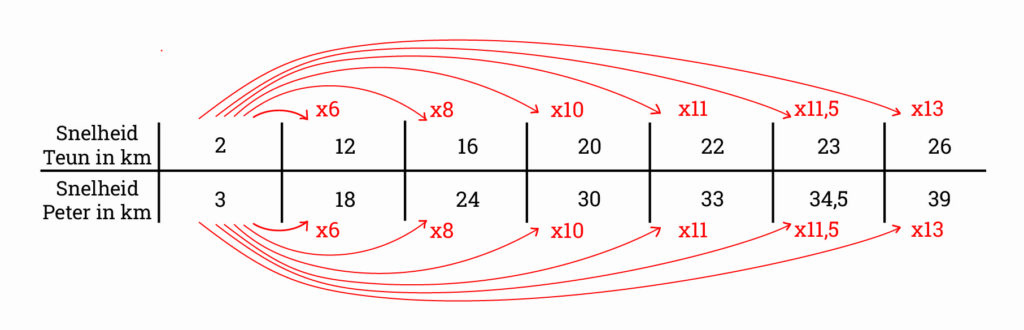
Veel sommen kunnen worden uitgerekend met een verhoudingstabel.
Bijvoorbeeld:
In het park is naast het fietspad een strook met rode en gele tulpen. Na 6 rode tulpen komen 4 gele tulpen. Er staan 54 rode tulpen in de strook naast het fietspad. Hoeveel gele tulpen staan er?
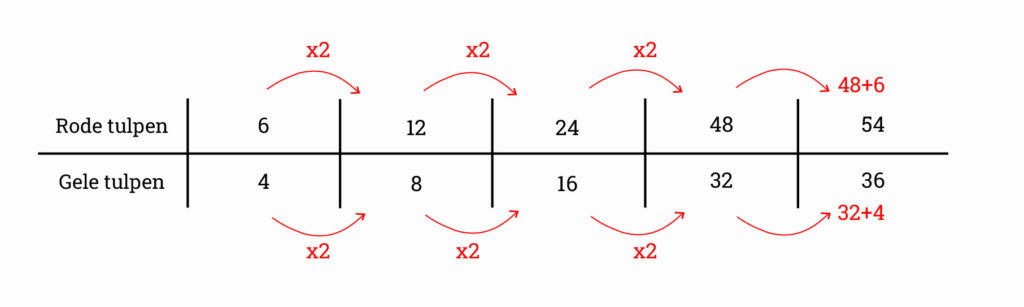
In bovenstaande is goed te zien hoe een verhoudingstabel werkt: je doet boven en onder altijd hetzelfde. Als je boven x 2 doet, doe je onder ook x 2. Als je de getallen in het vierde en het eerste hokje boven de streep bij elkaar optelt (in dit geval: 48 + 6) , tel je ook de getallen in het vierde en het eerste hokje onder de streep bij elkaar op (in dit geval: 32 + 4).
Verhoudingstabellen kun je ook gebruiken bij breuken.
Bijvoorbeeld:
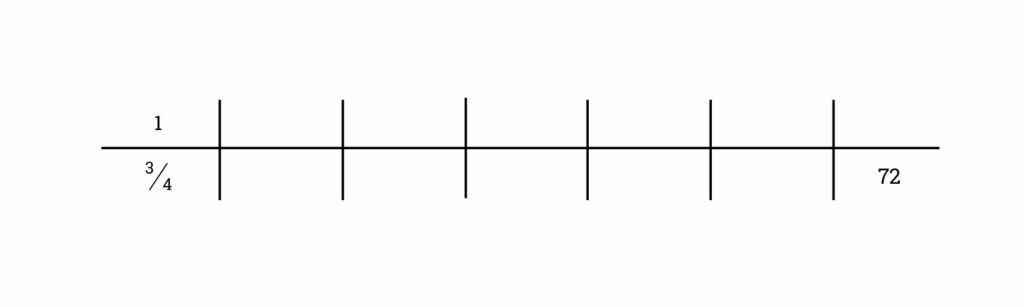
72 : ¾ =
Wat weten we? ¾ : ¾ = 1 (óf 1 x ¾ = ¾) dit is het begin van de verhoudingstabel
We willen niet weten hoeveel ¾ : ¾ is, maar we willen weten hoeveel 72 : ¾ is. We gaan dus van ¾ toewerken naar 72.
We vullen 72 vast in:
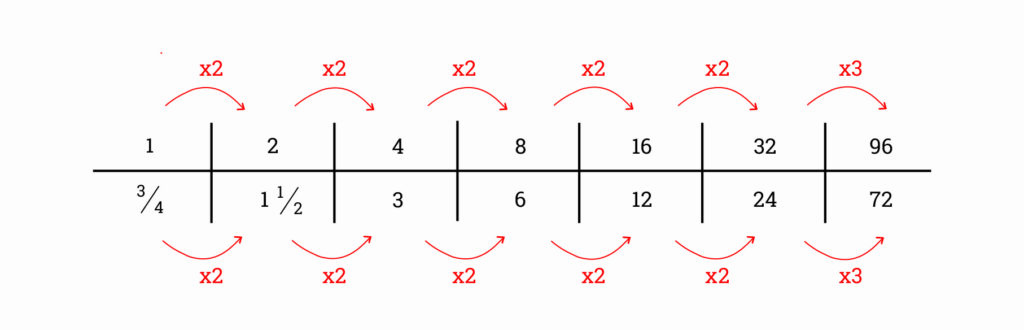
Wat maakt deze verhoudingstabel nu eigenlijk duidelijk?
¾ : ¾ = 1
1 ½ : ¾ = 2
3 : ¾ = 4
6 : ¾ = 8
12 : ¾ = 16
24 : ¾ = 32
72 : ¾ = 96
Nog een voorbeeld: 3 ¼ : 1/8.
In het vorige voorbeeld gingen we uit van ¾ : ¾ = 1. In dit voorbeeld draaien we het om: 1 x 1/8 = 1/8 (in plaats van 1/8 : 1/8 = 1).
1 x 1/8 = 1/8 dit vullen we in in de verhoudingstabel:

Verhoudingstabellen kun je ook gebruiken bij sommen die gaan over procenten en kommagetallen.
Bijvoorbeeld:
Tijdens een high tea worden er 48 kopjes thee gedronken. De inhoud van een kopje is 0,125 liter. In de waterkoker gaat 1,5 liter. Hoeveel keer moet de waterkoker worden gevuld?
Bij deze som is het handig om te weten: 0,125 = 1/8 (dit kun je zien in de tabel in het artikel over kommagetallen).

Het verhaaltje bij een verhaaltjessom zorgt vaak voor verwarring. Om de som overzichtelijk te maken, laat je het verhaaltje even weg en schrijf je alleen de getallen op die je hebt gekregen. In dit geval:
- 48 kopjes thee
- 1 kopje = 0,125 liter
- Waterkoker = 1,5 liter
De belangrijkste informatie waar we mee beginnen is: 1 kopje = 0,125. Deze informatie vullen we dus als eerste in in de tabel:
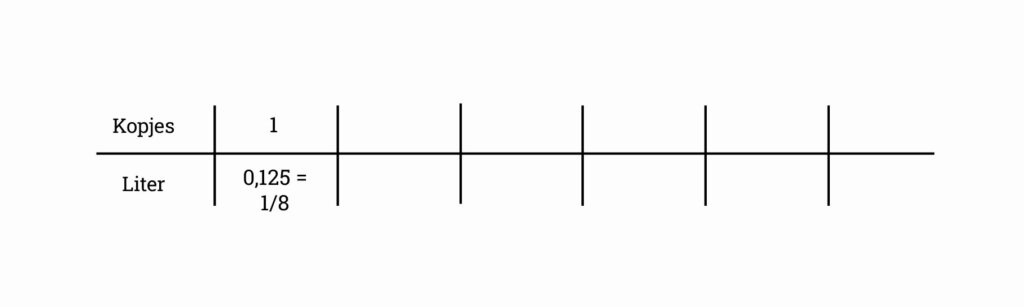
We willen weten hoeveel keer de waterkoker moet worden gevuld voor 48 kopjes. Dus 48 vullen we ook vast in, omdat we daar naartoe gaan werken.
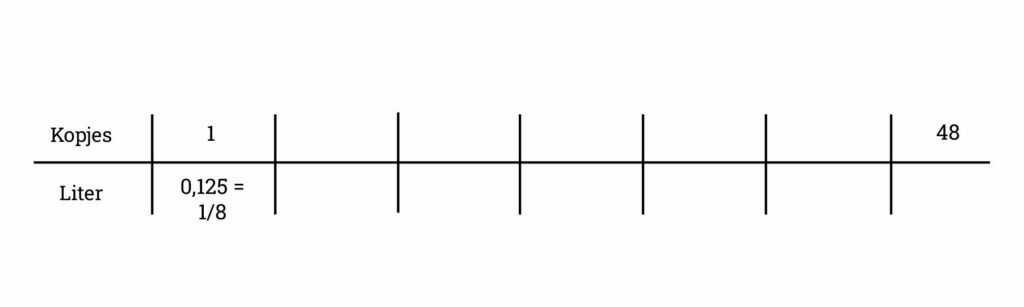
Verder is het belangrijk om te onthouden dat er 1,5 liter in de waterkoker gaat. Als we aan de onderkant 1,5 zien verschijnen, moeten we dus even extra opletten.
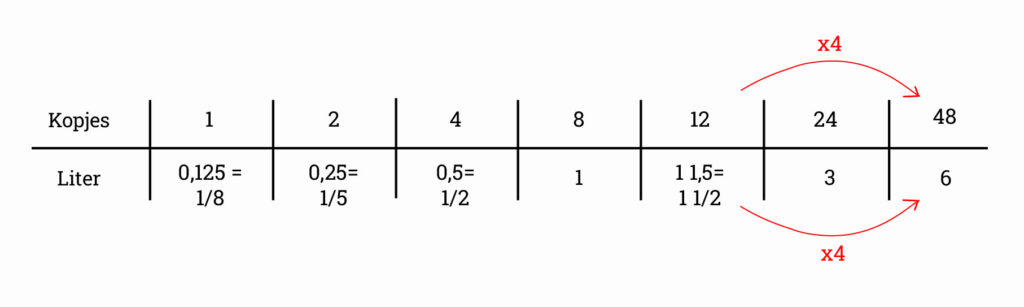
In de tabel zie je dat er 1,5 liter water nodig is voor 12 kopjes thee. Dus als we de waterkoker 1 keer hebben gevuld, hebben we 12 kopjes thee. We moeten de waterkoker dus 4 keer (1,5 x 4 = 6 liter) vullen om 48 kopjes thee te kunnen zetten.
Het maakt niet uit of je de kopjes of het aantal liters boven of onder in de tabel invult.
Dit artikel kun je hier als PDF downloaden: Verhoudingen PDF
Bekijk ook de uitgebreide uitleg over:
- het berekenen van procenten met een verhoudingstabel
- Verhoudingstabellen: een 8-stappenplan
-
Oefenboeken Doorstroomtoets Groep 8 deel 1 + deel 2
Oorspronkelijke prijs was: 54,00.39,95Huidige prijs is: 39,95. BUNDELKORTINGIn mijn winkelwagen Bekijk detailsJaarpakket Groep 8
Oorspronkelijke prijs was: 708,30.490,00Huidige prijs is: 490,00. Speciaal JaarpakketIn mijn winkelwagen Bekijk detailsRekenpakket Groep 6 – 2e helft schooljaar (Cito-IEP)
Oorspronkelijke prijs was: 59,90.54,00Huidige prijs is: 54,00. BundelkortingIn mijn winkelwagen Bekijk detailsCito E6 – IEP groep 6 pakket (2e helft schooljaar)
Oorspronkelijke prijs was: 59,90.54,00Huidige prijs is: 54,00. BundelkortingIn mijn winkelwagen Bekijk detailsGerelateerde artikelen
Reacties
25 reacties op “Verhoudingen berekenen: uitleg en voorbeelden”Geef een reactie




















Beste Carola,
Een vraag over definitie van ‘verhouding’. Als (a) in verhouding tussen (b) groter wordt, betekent dat het verschil tussen beide kleiner wordt?
Beste Joost,
Ik begrijp je vraag niet helemaal. Wellicht kun je een voorbeeld geven?
De Van Dale geeft de volgende definitie: getal dat de grootte van twee getallen ten opzichte van elkaar uitdrukt.
Bijvoorbeeld: Alex fietst 2 keer sneller dan Bram.
Als Alex 10 km/u fietst, fietst Bran 5 km/u.
Als Alex 3 keer sneller dan Bram fietst en Alex fietst 30 km/u, dan fietst Bram 10 km/u.
Ik hoop dat je hier iets aan hebt.
Hartelijke groet,
Carola de Koning
72/3:4= 72x 4:3 =828:3= 96
klopt, delen door een breuk is zelfde als vermenigvuldigen met de omgekeerde breuk, alleen 72×4=288 ipv 828
Het is heel leerzaam voor mijn kind.
Fijn om te horen Tarek. Dank voor je bericht.
Hartelijke groet,
Carola
Omwille van het `realistische rekenen` wordt het tabellenvoorbeeld van 72 : 3/4 = hier uitgelegd. Het laat echter de enorme (onnodige !) berg rekenwerk zien waar het `realistische rekenen` leerlingen mee belast.
De aloude, heel simpele (en héél snelle !) berekening van 72 : 3/4 = 72/1 x 4/3 = 288/3 = 96 is OOK goed uit te leggen en te visualiseren met een strookmodel.
Dat men het “traditionele rekenen” verwijt vooral te bestaan “uit onbegrepen trucjes”, is niet omdat dat oude rekenen “trucjes” bevat, maar omdat er leerkrachten zijn/waren die totaal geen idéé hadden hoe ze “delen door een breuk = vermenigvuldigen met het omgekeerde” moesten uitleggen/visualiseren en gedetailleerd opbouwen. Ook in 2018 geldt dat “niet begrepen rekentechnieken” een gebrek aan didactiek (!) is. De léérkracht maakt het verschil. Niet de rekentechniek.
Maaike laat in haar vele publicaties prima zien hoe je uitlegt. Complimenten dus!
Dank weer voor je bericht Peter! En dank voor je compliment!
Hartelijke groet,
Carola
ik snap het t/m de tulpen daarna begrijp ik er niks van heb je dat nog ergens uitgelegd? verder zijn we heel blij met de boeken van groep 7…wel mis ik meer uitleg hoe het beste te rekenen want er zijn meer wegen die naar Rome leiden. Vooral bij hoofdrekenen. groeten Carmen
Hallo Carmen,
Ik kan me voorstellen dat je dit lastig vindt. Als je het niet snapt, verzin dan een voorbeeld met kleinere getallen, je kunt bijvoorbeeld hele getallen gebruiken in plaats van breuken, en de som tekenen helpt ook vaak.
Fijn om te horen dat jullie zo blij zijn met de oefenboeken. Op de website vind je veel uitleg en tips. Mocht je toch nog vragen hebben, dan kun je ons altijd even e-mailen.
Succes!
Hartelijke groet,
Carola
De uitleg bij de tabellen met breuken is erg lastig voor leerlingen.
Uit ervaring is het geen probleem om deze op dezelfde manier op te lossen als de andere ( boven x6 dan beneden ook x6. Delen door een breuk kan(op een andere manier) geleerd worden zonder die tabellen. Dan geeft het geen verwarringen en kan ook de zwakkere leerling beide zonder problemen maken.
De uitleg is erg duidelijk, het is jammer dat dit niet te printen is , ik wilde het graag in mijn praktijk gebruiken maar wanneer ik print lopen de teksten door elkaar.
Hi José, ik heb onderaan het artikel een PDF toegevoegd. Je kunt op de link ‘verhoudingen PDF’ klikken om het PDF-bestand te openen en dan kun je het printen.
Hartelijke groet, Maaike
Super handig! Dit ga ik met mijn dochter doornemen.
Goede uitleg voor mijn oudste. Hij zit nu in groep 6, dit is toch ook stof die in groep 6 nog wordt behandeld.
Top
dankuwel, goed uitgelegd!
L.S.
Goede manieren om ze uit te leggen en een aardige mogelijkheid dat velen het begrijpen.
Bedankt!
Het is heel leerzaam voor mijn kind.
Goed uitgelegd en mooi oefenmateriaal.
Dank je wel!
Heel handig!
Heel handig! Dankjwel
Ikzelf vindt de breuken nog steeds lastig. Wel goed uitgelegd
De uitleg bij de verhoudingstabel als hulpmiddel bij breuken is verwarrend, omdat de dubbele punt (:) de ene keer betekent ‘staat tot’ en de andere keer ‘gedeeld door’.
Bij de overige voorbeelden is de uitleg wel duidelijk!
Eigenlijk betekent die dubbele punt in beide gevallen hetzelfde. Want 1 staat tot 6 betekent ook 1/6 (staat tot 1).