Realistisch rekenen: uitleg en voorbeelden

Realistisch rekenen is ontstaan in de jaren 70. Een Nederlandse wiskundige, Hans Freudenthal, vond dat rekenen minder abstract moest worden, zodat zoveel mogelijk kinderen de lastige rekenstof zouden snappen. Bij realistisch rekenen ligt de nadruk op inzicht.

Wil je meer weten over deze vorm van rekenonderwijs? Lees dan verder.

Wat is realistisch rekenen?

Realistisch rekenen is dus vooral in het leven geroepen om kinderen de rekenstof beter te laten begrijpen.

De bedoeling van realistisch rekenen is nog steeds dat je kind diverse rekenmethoden kan toepassen in concrete situaties. Daarvoor mag het zijn eigen inzichten en strategieën gebruiken.

Voor jonge kinderen geldt letterlijk dat zij sommen aangeboden krijgen die verpakt zitten in realistische context.

Bijvoorbeeld:

Ik heb 3 snoepjes. Jij hebt 2 snoepjes. Hoeveel snoepjes hebben we samen?

Bij realistisch rekenen is er veel ruimte voor de vorming van begrip.

Kinderen moeten begrijpen wat ze doen. Dat is volgens de grondlegger van deze methode beter dan klakkeloos aannemen dat een som ‘nu eenmaal op die manier’ uitgerekend moet worden.

Verschil realistisch en traditioneel rekenen

Laten we nog eens teruggaan naar het voorbeeld hierboven:

Ik heb 3 snoepjes. Jij hebt 2 snoepjes. Hoeveel snoepjes hebben we samen?

De traditionele rekenmethode zou hiervoor in de plaats de volgende som beantwoord willen zien:

3 + 2 =

Het verschil is meteen duidelijk: bij traditioneel rekenen gaat het om kale sommen. Sommen die meestal maar via 1 weg opgelost dienen te worden, terwijl er misschien wel veel meer mogelijkheden zijn.

Realistisch rekenen gaat juist uit van dat laatste: er zijn meerdere wegen die naar Rome leiden en daar mag je kind allemaal gebruik van maken. Zolang hij maar begrijpt wat hij moet doen om een alledaags probleem of vraagstuk op te lossen.

Bovendien willen de aanhangers van realistisch rekenen graag dat je kind écht begrijpt wat het doet.

Een voorbeeld: de staartdeling

Een mooi voorbeeld waarmee we het verschil tussen traditioneel rekenen en realistisch rekenen kunnen laten zien, is de staartdeling.

De traditionele staartdeling

Toen er nog enkel traditioneel gerekend werd, werd de staartdeling op deze manier aangeleerd (uitleg volgt onder de som):

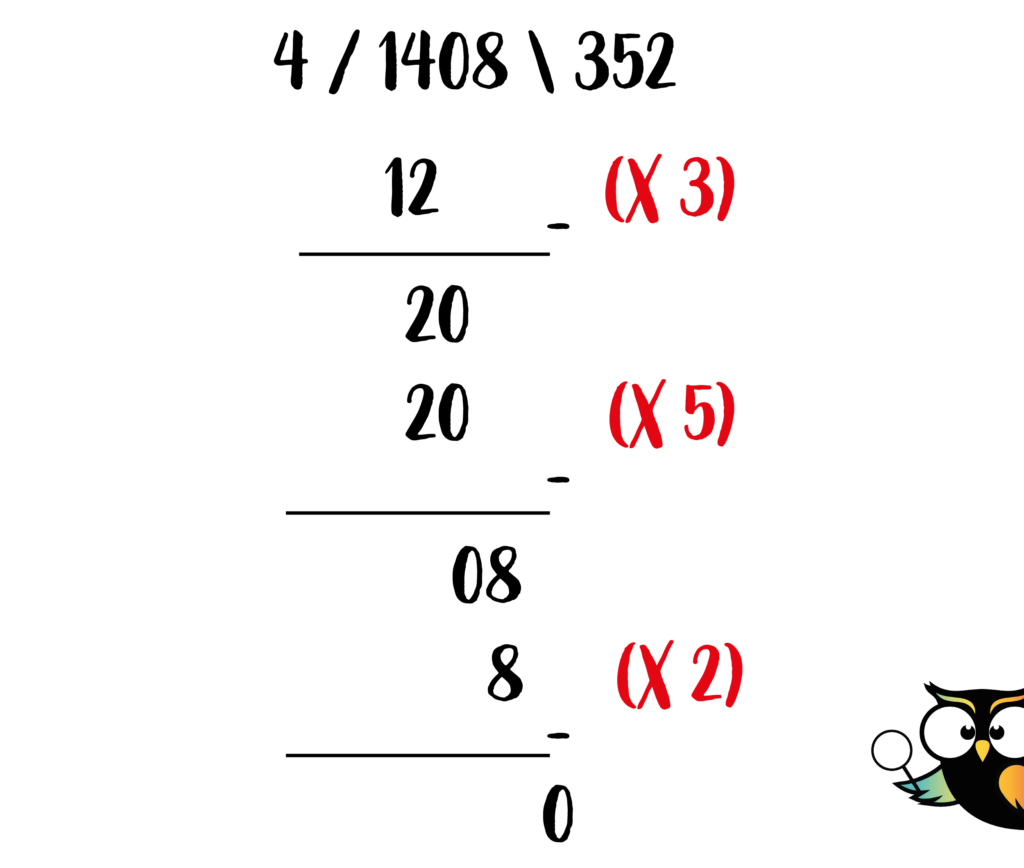
Je ziet hoe de stappen elkaar opvolgen in deze traditionele rekenmethode. Steeds moet je op zoek naar het eerste getal dat groter is dan 4. Je begint daarbij aan de linkerkant van het getal.

Je moet kijken welk getal (deelbaar door 4) daar het dichtste bij komt. Dat getal mag alleen kleiner of gelijk zijn aan het getal waarmee gewerkt wordt.

In dit voorbeeld wordt eerst met 14 gewerkt, omdat dat het meest linkse getal is. Het getal (deelbaar door 4) dat het dichtste bij 14 komt, is 12.

12 is 3 x 4. Daarom moet de 3 worden genoteerd als eerste cijfer van de uitkomst. De uitkomst staat aan de rechterkant van de staartdeling.

12 wordt nu van 14 afgehaald. Dan houd je 2 over. Vervolgens voeg je daaraan het eerstvolgende cijfer van het grote getal toe: 0. Samen vormen de 2 en de 0 nu 20.

Nu doe je precies hetzelfde als in de vorige stap: kijk welk getal (deelbaar door 4) het dichtst bij 20 komt. Dat is in dit geval 20 zelf. 20 : 4 = 5.

Schrijf de 5 achter de 3, als tweede cijfer van de uitkomst.

In de laatste stap doe je nog een keer hetzelfde. Uiteindelijk kom je tot een uitkomst van 352.

Op zich is deze vorm van staartdelen prima. Je kind maakt de som stap voor stap en komt uiteindelijk (als het goed is) tot de goede uitkomst.

Toch is bovenstaand voorbeeld een typische vorm van traditioneel rekenen. Je kind begrijpt waarschijnlijk weinig tot niets van de werkwijze.

Met andere woorden: het weet niet waarom het de som op deze manier aanpakt.

De kans is bovendien groot dat je kind geen idee heeft van eventuele foutjes die in de uitwerking sluipen. Dat is mede te wijten aan het feit dat je kind niet begrijpt wat het aan het doen is. In onderstaande video wordt de traditionele staartdeling nog eens uitgelegd.

De realistische staartdeling

De realistische rekenmethode wil juist wél dat je kind begrijpt hoe de gebruikte getallen zich tot elkaar verhouden. Daarom is de staartdeling op dat getalbegrip aangepast.

We doen dezelfde som nog eens, maar nu rekenen we hem uit via de realistische rekenmethode.

Je ziet dat deze staartdeling er qua structuur vrijwel hetzelfde uitziet als die in het voorbeeld van de traditionele rekenmethode.

Toch is de aanpak wezenlijk anders. Hoewel er nu ook getallen van het oorspronkelijke getal worden afgehaald, gaat je kind nu veel concreter zien waarom het antwoord daadwerkelijk kan kloppen.

In de eerste stap haal je 1200 van 1408 af. 1200 = 4 x 300. Dat betekent dat de uitkomst van de som dichtbij 300 moet liggen. 300 schrijf je rechtsboven in de staartdeling op als eerste deel van de uitkomst.

Vervolgens zoek je naar het getal (deelbaar door 4) dat het dichtst bij de overgebleven 208 ligt. Dat is 200. 200 = 4 x 50. Die 50 wordt opgeteld bij de 300 die al bij de uitkomst staat.

Als laatste doe je hetzelfde met de overgebleven 8.

Uiteindelijk levert deze methode dezelfde uitkomst op: 352. Deze manier van realistisch rekenen wordt ook wel de hapmethode genoemd. Je haalt namelijk steeds happen van het getal af.

Zoals je ziet zijn beide methodes goed. Je komt immers tot dezelfde uitkomst.

En ondanks dat de realistische methode wat meer vergt van de rekenvaardigheden van je kind (het moet werken met grotere getallen), snapt het wel beter waar de uitkomst vandaan komt.

Je kind doorziet de getallen waarmee het werkt. En daar gaat het om. Nu kan je kind gemakkelijk een vergelijkbare som zelfstandig oplossen en inschatten of de uitkomst klopt.

De principes van realistisch rekenen

Realistisch rekenen is ontstaan uit de waarnemingen van Hans Freudenthal. Toen hij het traditionele rekenonderwijs onder de loep nam, zag hij dat kinderen nauwelijks rekeninzicht ontwikkelden.

De regels die ze moesten toepassen, gebruikten ze alleen in sommen die sterk overeenkwamen met de sommen die ze geleerd hadden.

Week een vraagstuk daarvan af, dan wisten nog maar weinig kinderen tot een oplossing te komen.

Bovendien waren de rekenlessen op school en het leven van alledag 2 totaal verschillende werelden.

Volgens Freudenthal en een aantal van zijn collega-onderwijsontwikkelaars moest daar verandering in komen.

Realistisch rekenen: een overzicht

Tegenwoordig zijn de principes van realistisch rekenen vergelijkbaar met die van de jaren 80:

• Er wordt nu veel vaker gewerkt met gewichten, bedragen en maten. Je kind krijgt daardoor een beeld bij de sommen die het uitrekent.

• Om ervoor te zorgen dat ook jonge kinderen al iets van rekenvaardigheden snappen, moet de stof op die leeftijd zo concreet mogelijk aangeboden worden. In plaats van 3 + 5 = wordt nu gevraagd hoeveel snoepjes Dinah en Tijn samen hebben.
  
• Het abstractieniveau mag toenemen naarmate het kind ouder wordt. Waar in de kleuterklas alleen nog gewerkt wordt met concrete voorbeelden, kan een kind eind groep 3 al prima rekenen met simpele getallen.
  
• Realistisch rekenen gaat over zingeving. Kinderen moeten begrijpen wat de betekenis is van de som, de werkwijze en de uitkomst.
  
• In veel gevallen wordt context aan een som toegevoegd, zodat die wat meer gaat leven voor kinderen. De context is het verhaaltje dat om de som heen is geschreven. We kennen dit soort contextrijke sommen ook wel als redactiesommen.
  
• Tijdens realistisch rekenen worden niet altijd alleen maar de rekenvaardigheden ontwikkeld. Meestal is er een overlap met andere vakgebieden, zoals taal, knutselen of aardrijkskunde.

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

Kenmerken realistisch rekenen

Wanneer een leerkracht werkt met de realistische rekenmethode, kun je een aantal kenmerken herkennen.

• Begrijpen is belangrijker dan continu dezelfde sommen maken.
• Minder nadruk op parate rekenkennis, zoals de tafels.
• De rekenmachine wordt vaker gebruikt.
• Kolomsgewijs rekenen wordt vaker toegepast dan cijferend rekenen.
• De staartdeling wordt nu gedaan met behulp van de hapmethode.
• In 1 rekenles kunnen meerdere onderwerpen aan bod komen.
• Kinderen leren handig rekenen.

Handig rekenen

Handig rekenen houdt in dat je kind methodes leert die op logica en handigheid gericht zijn.

Bijvoorbeeld bij deze som:

Cynthia heeft 13 koekjes verkocht.
Lex heeft er 8 verkocht.
Mascha heeft er 7 verkocht.

Hoeveel koekjes hebben de kinderen in totaal verkocht?

Bij handig rekenen kijkt je kind eerst naar de getallen die je op een makkelijke manier kunt verwerken. In deze som is het bijvoorbeeld handiger om eerst 13 + 7 te doen en daarna pas de 8 bij de uitkomst op te tellen.

13 + 7 komt immers uit op een tiental. Bij 13 + 8 moet je over een tiental heen rekenen. Dat is dus moeilijker.

Als je kind eerst 13 + 7 uitrekent, kan het de moeilijkere som uit de weg gaan. Daarom wordt deze methode ook wel handig rekenen genoemd.

Voorbeelden van realistisch rekenen

Er zijn eindeloos veel voorbeelden van realistisch rekenen. Hieronder geven we er een paar.

Verschillende werkwijzen gebruiken

Jana heeft 4 appels.
Brent heeft ook 4 appels.
Yula heeft ook 4 appels.

Hoeveel appels hebben deze 3 kinderen samen?

Deze som is een typisch voorbeeld van realistisch rekenen. Je kind moet werken met een alledaagse situatie en mag vervolgens helemaal zelf bepalen hoe het de som oplost.

Zo kan het ervoor kiezen deze werkwijze te gebruiken:

4 + 4 = 8
8 + 4 = 12

Ook kan je kind ervoor kiezen direct een keersom te maken van de vraag:

3 x 4 = 12

Nogmaals, het maakt bij realistisch rekenen niet uit voor welke werkwijze je kind gaat. Waar het om draait is dat het tot een correct antwoord komt op een manier die hij zelf begrijpt.

Nog een voorbeeld:

Benthe heeft 8 spekjes.
Youssef heeft 5 spekjes.

Hoeveel appels hebben Benthe en Youssef samen?

Misschien vindt je kind het lastig om direct over een tiental heen te rekenen. Dan hakt het de som in stukjes.

Eerst doet het 8 + 2 = 10.
Vervolgens kijkt je kind hoeveel spekjes er nog over zijn van de oorspronkelijke 5. Dat zijn er 3.

10 + 3 = 13.

Een ander kind vindt het misschien helemaal niet moeilijk om over het tiental heen te rekenen. Hij rekent direct 8 + 5 = uit. Met dezelfde uitkomst tot gevolg: 13.

Bussommen

In groep 3 wordt veel gewerkt met bussommen. In die sommen is letterlijk een plaatje van een bus zichtbaar. In de bus zitten mensen. Bij sommige haltes stappen mensen uit, bij andere stappen juist mensen in.

Bussommen zijn een goed voorbeeld van de realistische rekendidactiek. Kinderen krijgen een heel helder beeld van wat er gevraagd wordt. Door het verhaaltje is de som veel concreter dan bijvoorbeeld 4 + 2 =.

Gedurende het jaar wordt de som steeds wat abstracter afgebeeld. Langzaam maar zeker werkt je kind toe naar een rekensom met echte getallen.

Redactiesommen

De zogenaamde redactiesommen zijn ook een goed voorbeeld van realistisch rekenen.

Doordat een som in een verhaaltje wordt gegoten, ziet je kind sneller in waarom het handig is dit soort berekeningen te kunnen maken.

Een kind dat alleen maar kale sommen voorgeschoteld krijgt, zal zich sneller afvragen wat het nut van die sommen is.

Een som die gaat over pannenkoeken bakken en de juiste hoeveelheden bloem, ei en melk spreekt veel meer tot de verbeelding. Sterker nog, zo’n som zet je kind misschien wel aan zelf lekker in de keuken aan de slag te gaan!

Voordelen van realistisch rekenen

Zoals je hierboven hebt kunnen lezen, zitten er aan realistisch rekenen heel wat voordelen. We zetten ze nog even voor je op een rijtje:

Je kind…

• krijgt een beter getalinzicht.
• begrijpt echt wat het doet als het een som uitrekent.
• wordt beter in schattend rekenen, verhoudingen, breuken, rekenen met procenten en hoofdrekenen.
• kan rekensommen in het dagelijks leven ook toepassen.

Nadelen van realistisch rekenen

Ondanks alle voordelen klinkt er ook kritiek als het over realistisch rekenen gaat.

Volgens deskundigen is deze vorm van rekenen vooral geschikt voor de betere rekenaars. De zwakkere rekenaars raken in de war door de grote hoeveelheid trucjes en werkwijzen.

Deze laatste groep heeft meer behoefte aan een eenduidige, gestructureerde aanpak. Traditioneel rekenen sluit daar dus beter op aan.

Een ander nadeel is dat kinderen minder goed worden in kale sommen maken (bijvoorbeeld 15 + 9 =). Kinderen die alleen gewerkt hebben met realistisch rekenen, zijn gewend om met verhaaltjes te werken.

Dat resulteert in slechtere scores voor cijferen bij optellen, aftrekken, vermenigvuldigen en delen.

Realistisch rekenen nu en in de toekomst

Er zijn in Nederland veel methodes die de didactiek van realistisch rekenen gebruiken. Een paar voorbeelden:

• Pluspunt (Malmberg)
• De wereld in getallen (Malmberg)
• WizWijz (Zwijsen)

Omdat wetenschappelijk onderzoek in de afgelopen jaren uitwees dat realistisch rekenen niet enkel positieve gevolgen had, hebben steeds meer methodes ook weer wat traditionele oefeningen toegevoegd.

Op deze manier worden zowel de sterke als de zwakke rekenaars uitgedaagd op hun eigen niveau.

Sommige nieuwe methodes zijn zelfs grotendeels teruggekeerd naar het traditioneel rekenen. Toch is het de vraag of dat slim is. Ook traditioneel rekenen leverde in het verleden problemen op.

In de toekomst zal de nadruk steeds blijven verschuiven. De maatschappij is in ontwikkeling en parallel daaraan beweegt het rekenonderwijs mee.

Wetenschappelijk onderzoek uit 2008 toont overigens aan dat het rekenniveau van kinderen niet afhankelijk is van de wijze waarop de sommen worden aangeboden.

Realistisch rekenen oefenen

Wil jij samen met je kind realistisch rekenen nog eens oefenen? Of willen jullie wat extra uitleg?

Check dan het YouTube-kanaal van Wijzer over de Basisschool. Je vindt hier filmpjes over diverse rekenonderwerpen. Superhandig!

Oefenen doe je met onze oefenboeken rekenen. Deze oefenboeken zijn allemaal toegespitst op het niveau van een bepaald leerjaar. Je vindt er vele verschillende sommen in terug, waaronder redactiesommen en andere vormen van realistisch rekenen.

Wacht dus niet langer en ga lekker thuis aan de slag met dit leuke rekenonderdeel!

Maaike de Boer, MA

drs. Maaike de Boer is initiatiefneemster van Wijzeroverdebasisschool.nl

Over Maaike