Kolomsgewijs delen met de hapmethode

In dit artikel vertellen we je hoe je deelsommen met de hapmethode uitrekent. Dit wordt ook wel kolomsgewijs delen genoemd.

Als je alles hebt doorgelezen, weet je:

• hoe je een deelsom met behulp van de hapmethode uitrekent;
• hoe je een deelsom met een deler groter dan 10 uitrekent met de hapmethode;
• hoe je een deelsom met rest uitrekent met de hapmethode;
• wat ‘kolomsgewijs delen’ betekent.

We hebben dus genoeg te vertellen! Lees je met ons mee?

Bekijk ook:

• Kolomsgewijs rekenen
• kolomsgewijs optellen
• kolomsgewijs aftrekken
• kolomsgewijs vermenigvuldigen
• Staartdeling
• Rekenen oefenen met de beste handleiding voor ouders

De hapmethode

De hapmethode is kenmerkend voor realistisch rekenen en is een manier om deelsommen uit te rekenen. Natuurlijk zijn er een heleboel verschillende manieren om dat te doen, maar in dit artikel gaat het vooral over deze hapmethode.

De hapmethode is overigens een andere naam voor ‘kolomsgewijs delen’. Als je daar iets over leest, weet je vanaf nu dat het over dezelfde methode gaat.

Maar waarom is het nu zo handig om de hapmethode goed te snappen?

Een kleine deelsom, zoals 16 : 2, is niet zo moeilijk. Die kun je wel uit je  hoofd uitrekenen. Dat geldt bijvoorbeeld ook voor 72 : 9.

Maar als je de deelsom 4.578 : 35 moet uitrekenen, wordt dat toch wel een beetje moeilijker. Gelukkig kun je zo’n som met de hapmethode wél zelf, uit je hoofd, uitrekenen.

Hoe je dat doet, laten we je verderop in dit artikel zien.

Maar eerst even dit:

Bij een deelsom wil je altijd weten hoe vaak het getal waardoor je gaat delen, in het grote getal past.

Kijk maar eens naar deze gemakkelijke som:

16 : 2 =

Het antwoord is 8, omdat de 2 in totaal 8 keer in de 16 past.

Bij de grotere deelsommen wil je eigenlijk hetzelfde weten: hoe vaak past het kleine getal in het grote?

Kijk maar eens mee naar deze deelsom:

484 : 4 =

Je wilt dus weten hoe vaak de 4 in 484 past. De uitkomst ga je berekenen met de hapmethode.

Werken met de hapmethode, hoe doe je dat?

Bij de hapmethode is het de bedoeling dat je altijd een veelvoud van het getal waar je door deelt, weghaalt uit het eerste getal. Dat klinkt nogal ingewikkeld…

Laten we het anders zeggen: je neemt steeds een hap uit het grote getal. Uiteindelijk werk je altijd zo dicht mogelijk naar de 0 toe.

We laten je zien hoe dat werkt.

Allereerst schrijf je de deelsom op een kladblaadje. Je kunt het beste  werken met ruitjespapier, want dan kun je de getallen netjes in de hokjes schrijven.

Daarna teken je het hapmodel erbij.

Het hapmodel kan op verschillende manieren getekend worden.

Bijvoorbeeld op deze 2 manieren:

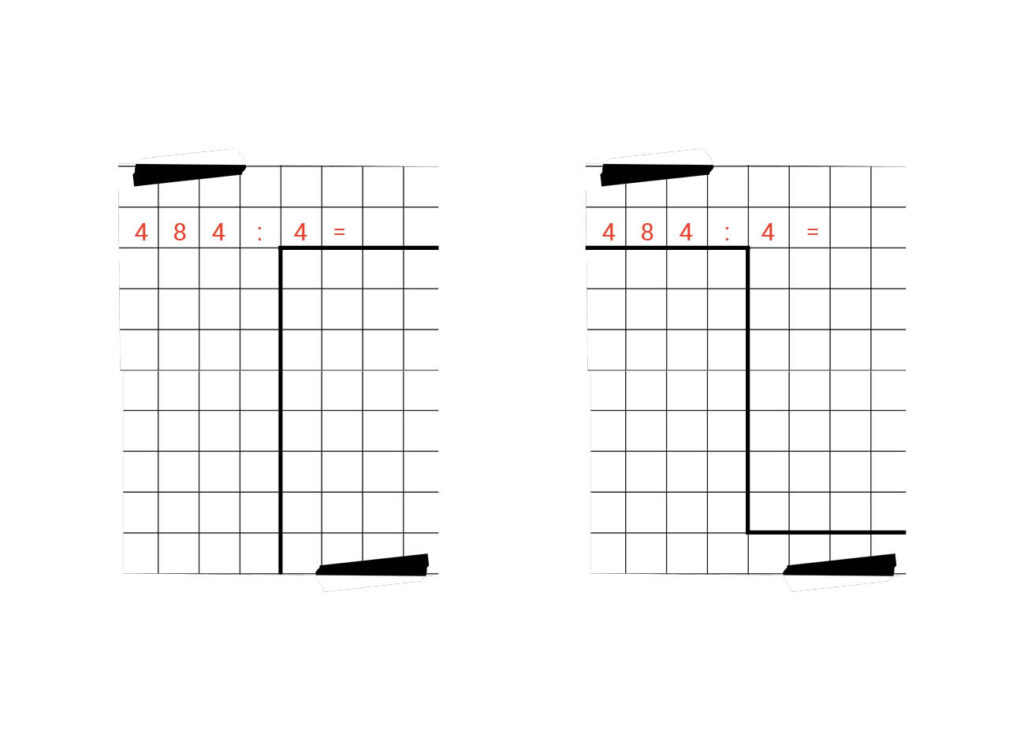
Er zijn nog meer verschillende manieren. Alle modellen werken op dezelfde manier, alleen schrijf je het steeds iets anders op.

In dit artikel gebruiken we steeds deze manier:

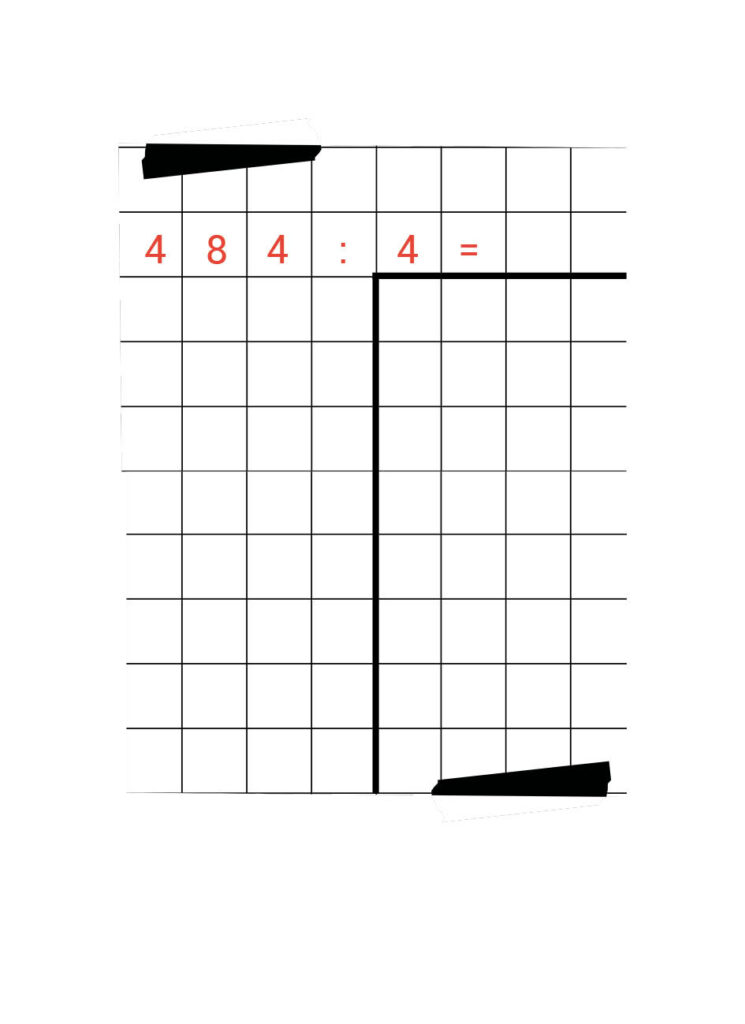
484 : 4 =

Ons hapmodel staat intussen klaar. Voordat we beginnen met het invullen van het hapmodel, maken we altijd op ons kladblaadje een geheugensteuntje.

We schrijven op ons blaadje een aantal keersommen van de tafel van 4 op.

Waarom we kiezen voor de tafel van 4?

Omdat we in deze som het grote getal gaan delen door 4. Dit geheugensteuntje gaat ons dadelijk helpen met het uitrekenen van moeilijke sommen. Daar komt het geheugensteuntje.

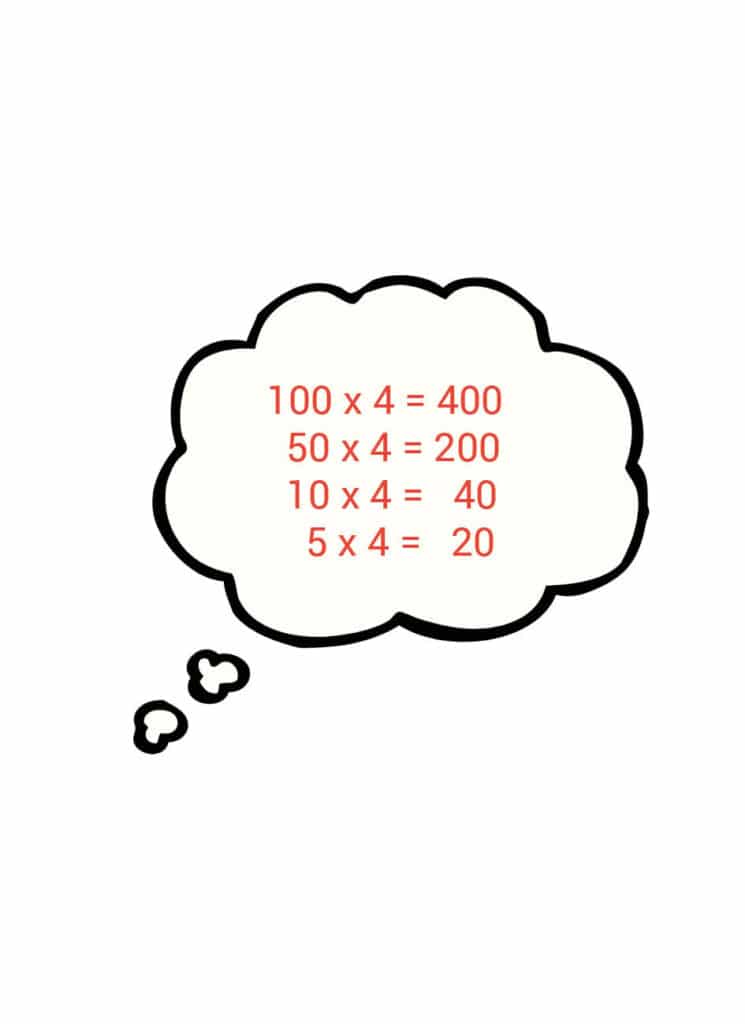
Je ziet dat we gekozen hebben voor x 100, x 50, x 10 en x 5. Dat mag je onthouden voor andere keersommen. Deze mogen er altijd in staan. Uiteraard verandert wel het getal waarmee je vermenigvuldigt bij een andere som.

Nu is het tijd om te bekijken hoe vaak 4 in 484 past. Dat doen we met behulp van ons geheugensteuntje.

Daar zie je staan: 100 x 4 = 400. Dat is een mooie eerste stap om te gebruiken.

Je ‘hapt’ nu 400 uit 484. Daarvoor schrijf je netjes 400 onder de 484. Daaronder zet je een streep en een minteken. Kijk, zo:

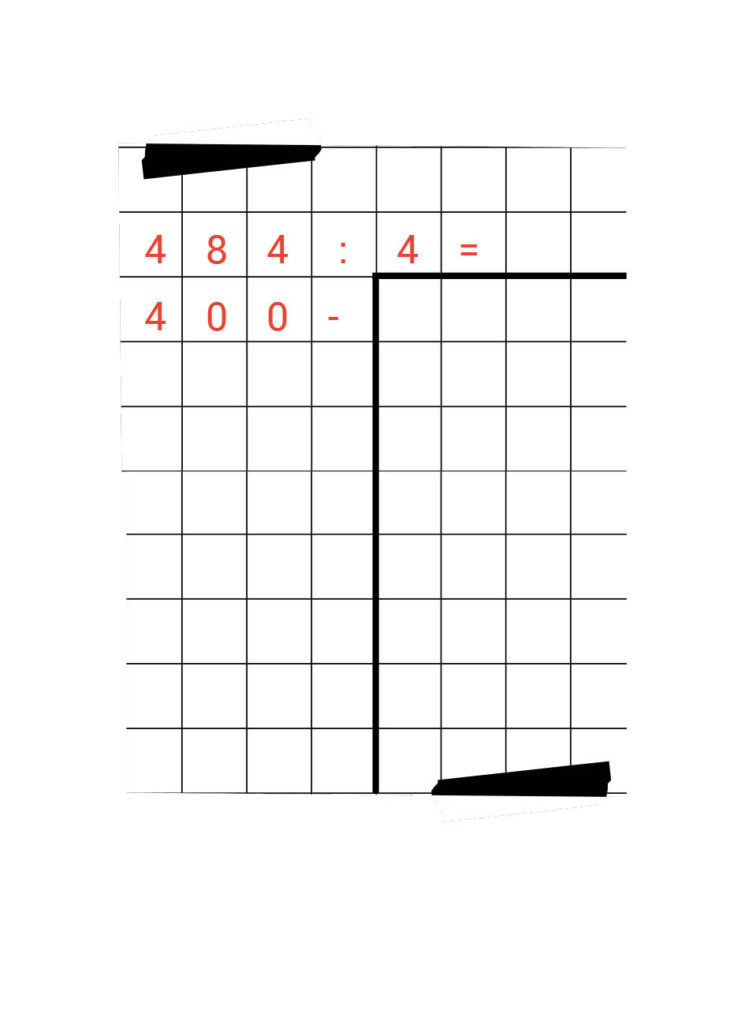
Naast 400 schrijf je vervolgens ‘100 x’. Daarna haal je 400 af van 484. Dan hou je 84 over.

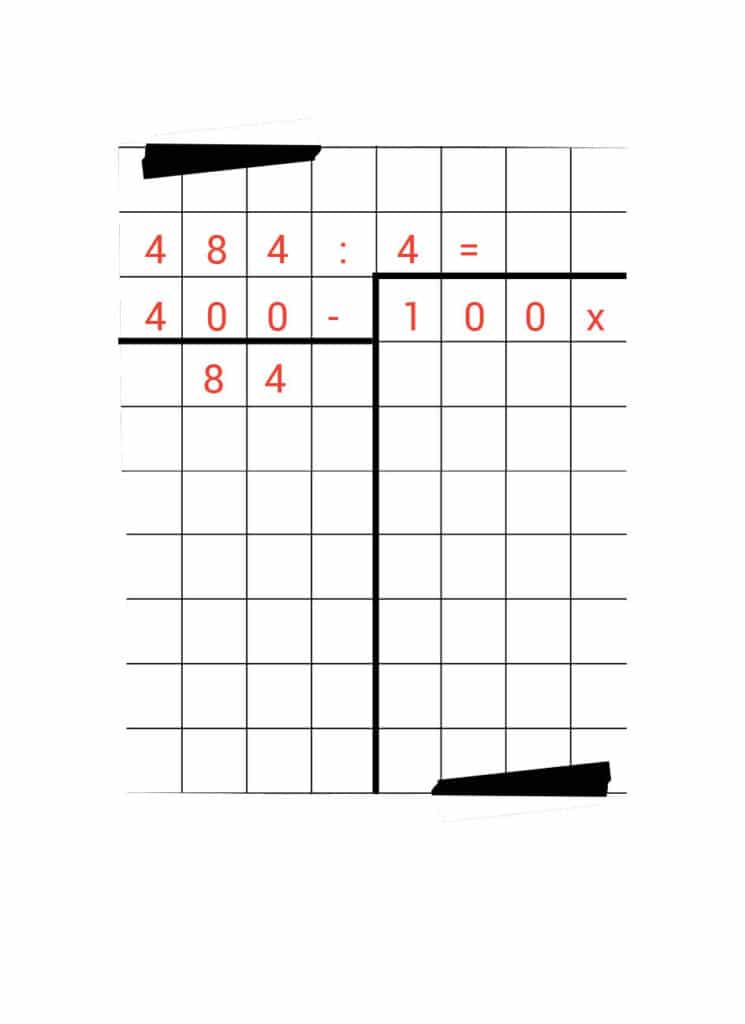
Nu wil je natuurlijk weten hoe vaak 4 nog in 84 past. We kijken daarvoor weer naar ons geheugensteuntje. Daar zien we bij 10 x 4 de uitkomst 40 staan. Die kunnen we uit de 84 ‘happen’.

Schrijf 40 onder 84 en zet er 10 x naast. Zo weet je welke stap je hebt gezet. Daarna maak je de minsom.

84 – 40 = 44

In ons schema zien deze stappen er zo uit:

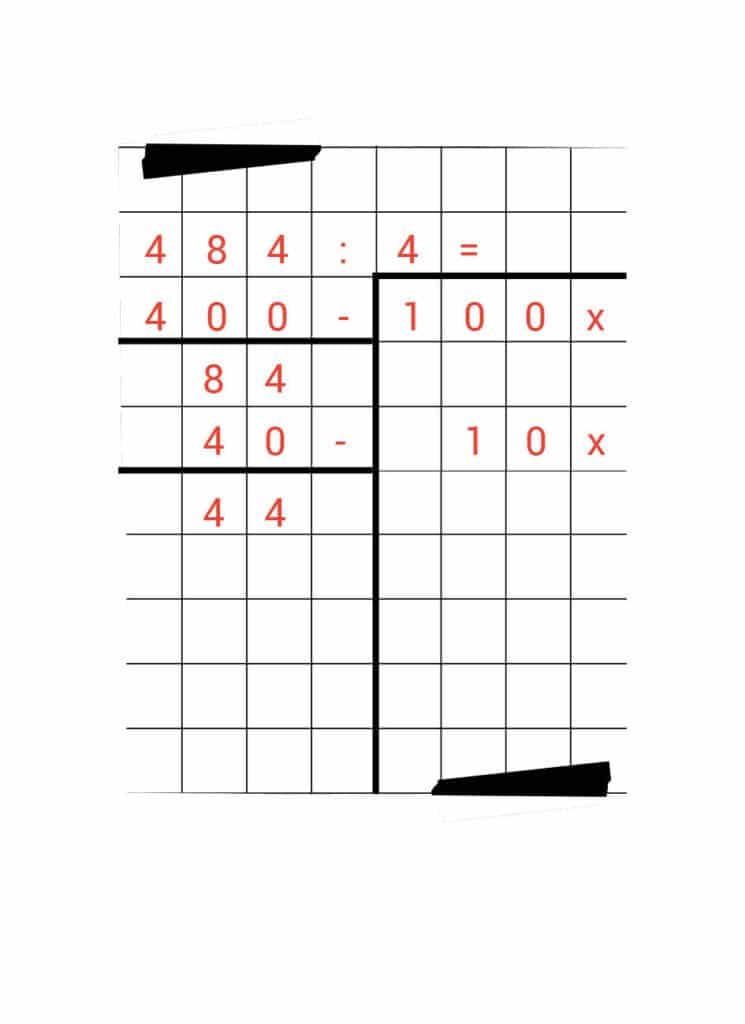
Nu is het de vraag hoe vaak 4 nog in 44 past. In ieder geval 10 x. We schrijven 40 op onder de 44 en zetten er 10 x naast. We maken weer de minsom en komen daarbij uit op 4.

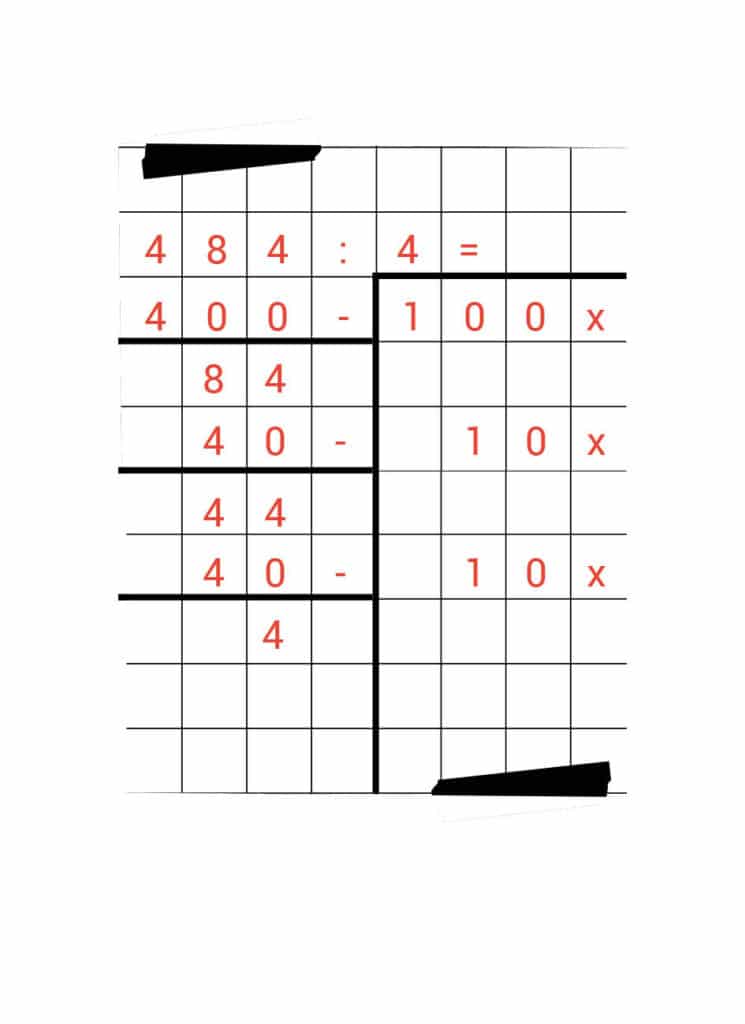
Nu willen we weten hoe vaak 4 nog in 4 past. Dat is natuurlijk niet zo moeilijk: dat past 1 keer.

We schrijven de 4 op en we zetten 1 x ernaast.

De minsom die we moeten uitrekenen, levert ons een uitkomst van 0 op.

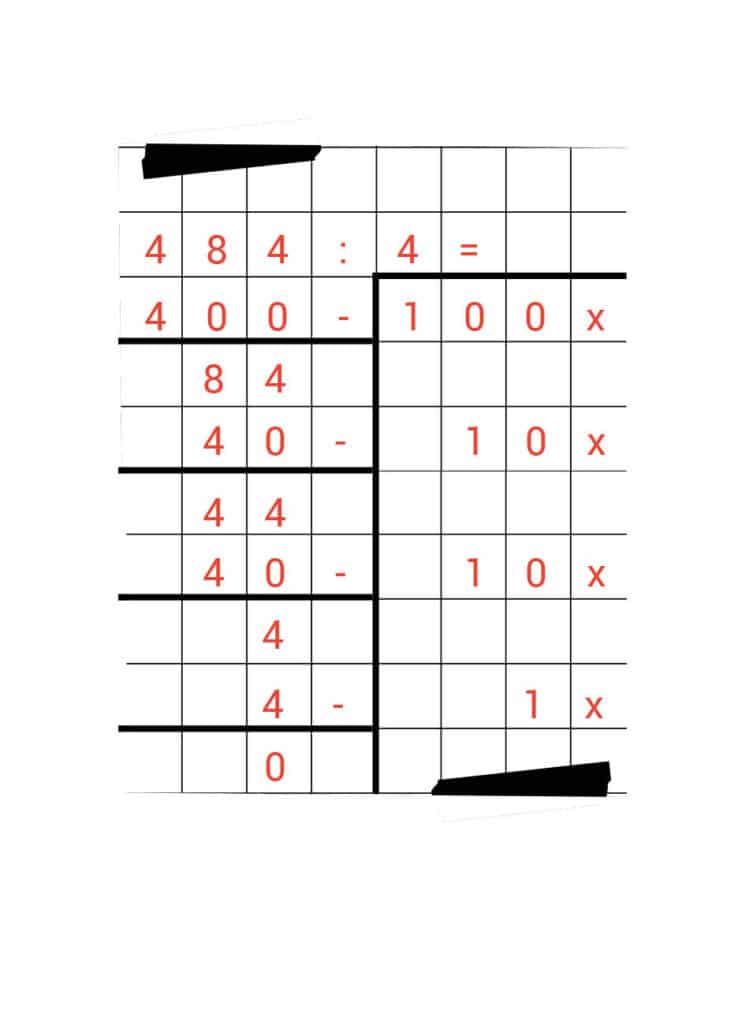
We zijn nu klaar met de deelsom, want we zijn op de 0 uitgekomen. Maar wat is nu de uitkomst van de som 484 : 4?

Voor de uitkomst moet ik alle getallen die ik net aan de rechterkant heb opgeschreven, bij elkaar optellen. Dan krijg je dus deze som:

100 + 10 + 10 + 1 =

De uitkomst van deze optelsom is 121. Dat betekent dat 4 ook 121 keer in 484 past!

484 : 4 = 121.

Zo, deze deelsom is nu af. Ons papier ziet er nu uit zoals je hierboven ziet, omdat wij deze keuzes hebben gemaakt bij het ‘happen’. De keuzes die jij maakt, kunnen totaal anders zijn.

Daarom kan deze som er voor iedereen anders uit zien. Wij zijn bijvoorbeeld begonnen met 100 x. Daarna gingen we door met 10 x en nog 10 x.

Maar misschien had jij wel in één keer 20 x willen doen. Dat mag natuurlijk ook! Doe wat voor jou handig is.

De uitkomst is uiteindelijk voor iedereen hetzelfde. Tenminste, als je nergens een rekenfoutje maakt!

De hapmethode met een deler groter dan 10

We doen nog een som. Maar nu is dat er eentje met een deler boven de 10.

Dit is de som:

4.380 : 12 =

Ter voorbereiding op ons rekenwerk tekenen we eerst ons schema.

En we maken ons geheugensteuntje. Omdat we nu gaan delen door 12, willen we weten hoe vaak de 12 in 4.380 past. Daarom maken we ons geheugensteuntje met de tafel van 12.

Onze voorbereiding ziet er dan zo uit:

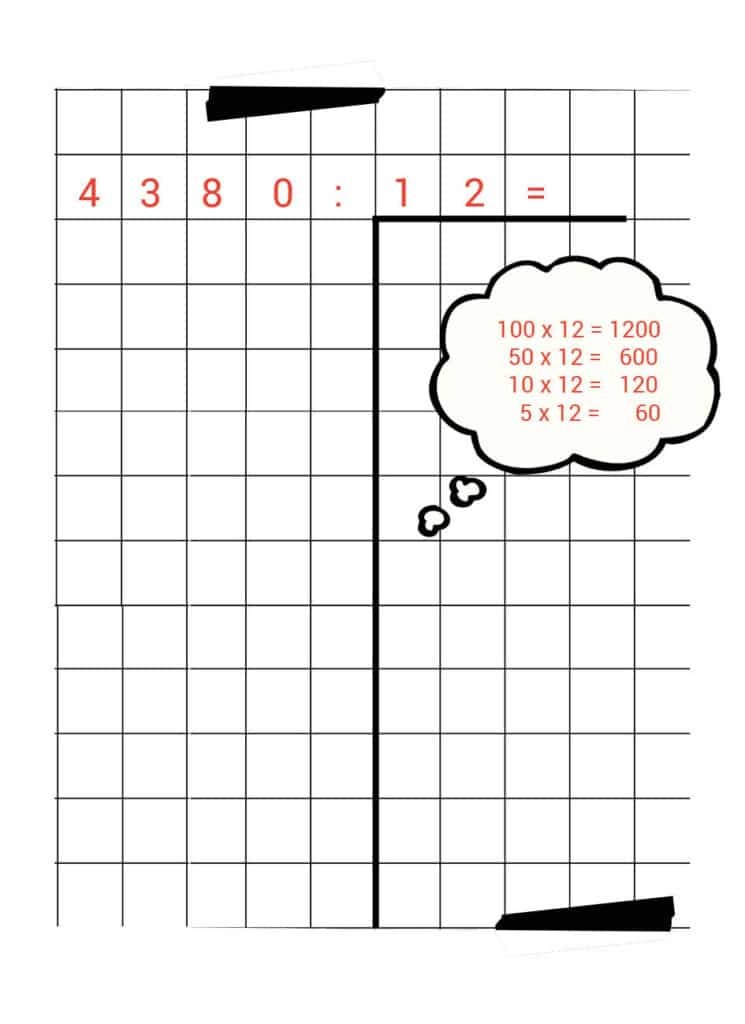
Zo, nu kunnen we beginnen.

We willen dus weten hoe vaak de 12 in 4.380 past. Daarvoor kijken we naar ons geheugensteuntje.

We beginnen met 100 x. Dat is 1200.

Schrijf 1200 netjes onder 4380 en reken meteen de minsom uit. Vergeet ook niet het getal 100 in de kolom rechts te plaatsen.

4380 – 1200 = 3180

Dit getal zetten we weer mooi onder de streep.

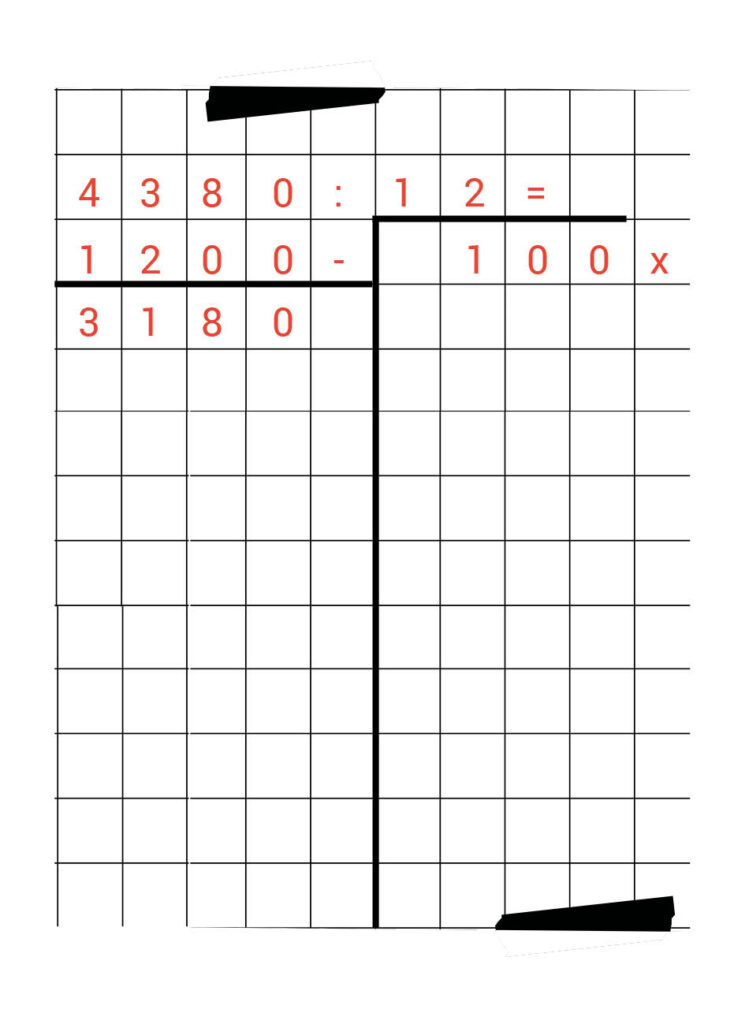
Nu willen we weten hoe vaak 12 in 3.180 past.

We kunnen natuurlijk nog een keer 100 x doen. Maar als je goed kijkt, zie je dat het dubbele ook kan. 200 x past ook!

200 x 12 = 2400

We halen nu dus 2400 af van 3.180. Dan houden we 780 over.

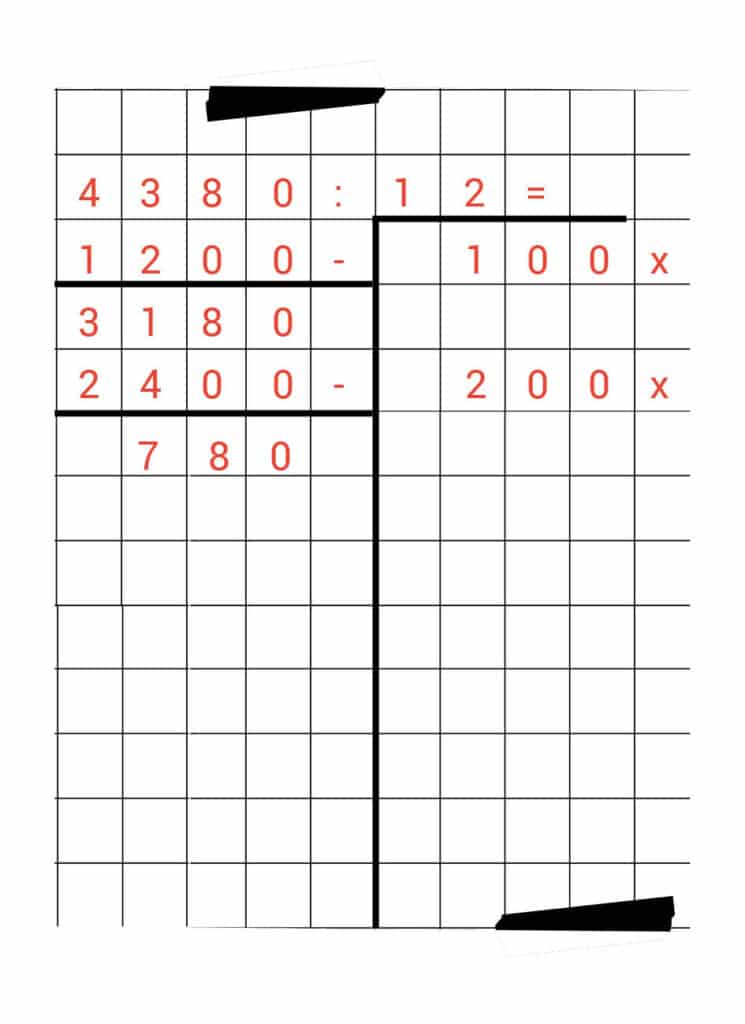
En zie je wat we met die 200 x hebben gedaan? Die staat weer netjes in de rechterkolom.

De volgende stap: hoe vaak past 12 nog in 780? Daarvoor kijken we nog eens naar ons geheugensteuntje.

We zien daarin dat 50 x 12 hetzelfde is als 600. Dat getal komt al aardig dicht bij 780. We kunnen het dus mooi gebruiken.

780 – 600 = 180

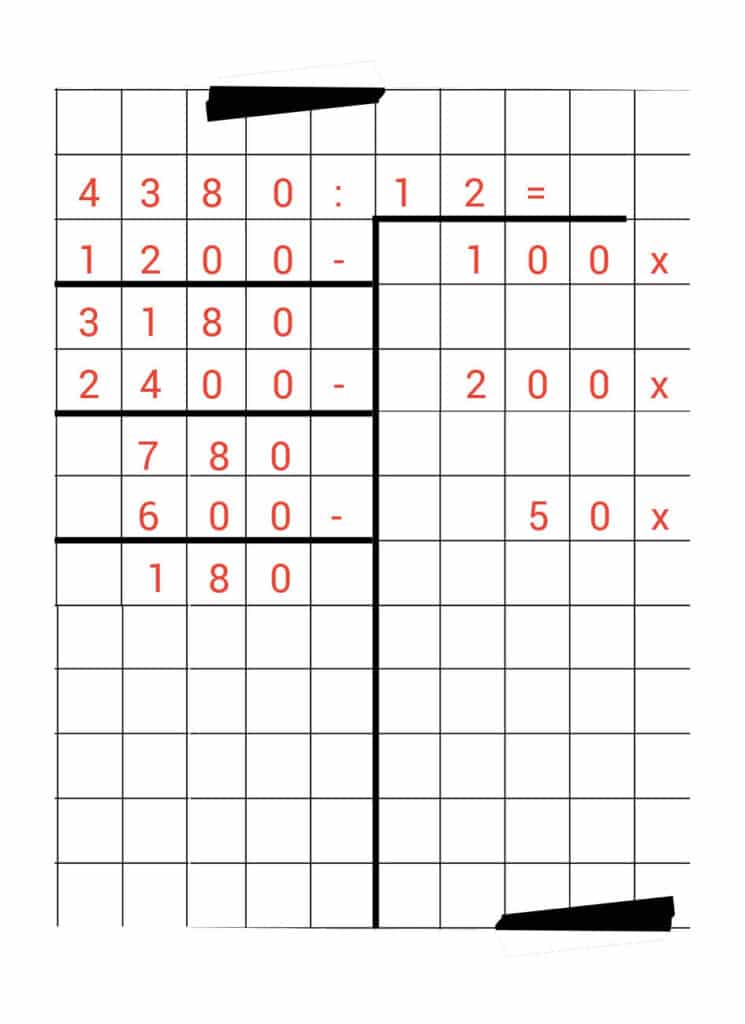
Hoe vaak past 12 nog in 180? Dan kan nog 10 keer.

We vullen daarom 120 in in de linkerkolom en 10 x in de rechterkolom.

Als we de minsom uitrekenen, houden we nog 60 over.

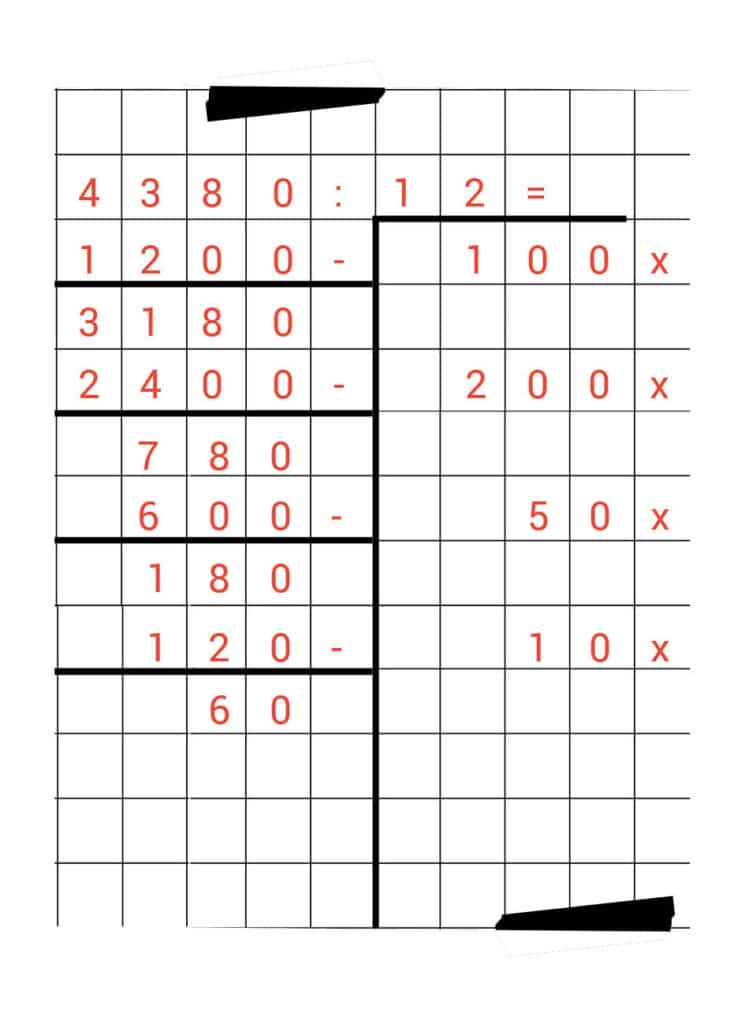
Als we kijken naar ons geheugensteuntje, dan zien we dat 5 x 12 nu nog precies past. Dat is namelijk 60.

Met deze laatste minsom komen we precies uit op nul.

Kijk maar:

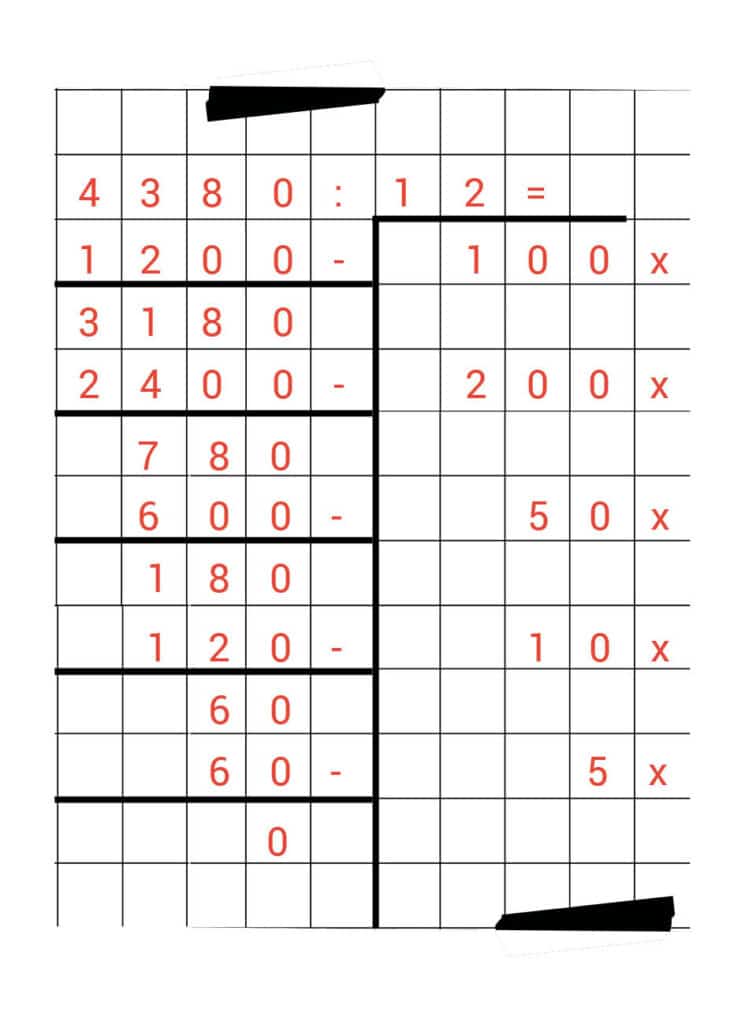
Dit betekent dat we nu klaar zijn met happen. Weet jij nog wat de volgende stap is?

Juist, we tellen alles aan de rechterkant bij elkaar op.

100 + 200 + 50 + 10 + 5 = 365

Het antwoord is dus 365.

4.380 : 12 = 365

Een deelsom met rest

We hebben je nu laten zien hoe je een deelsom oplost met behulp van de hapmethode. Ook hebben we je laten zien hoe je de hapmethode gebruikt als het getal waardoor je deelt groter is dan 10.

Intussen weet je ook dat het voor dit soort sommen het handigst is om  ruitjespapier te gebruiken. Zo kun je altijd netjes werken en heb je mooi de ruimte om je geheugensteuntje op te schrijven.

We willen je nu nog 1 soort som laten zien. Dat is een deelsom die niet precies op een heel getal uitkomt.

Als de hapmethode onderaan niet precies eindigt op een 0, dan noemen we dat een deelsom met rest. Hoe je die uitrekent, laten we je nu zien.

Dit is de som:

4.578 : 25 =

Doe je met ons mee? Schrijf eerst de hapmethode op je blaadje en maak daarnaast je geheugensteuntje.

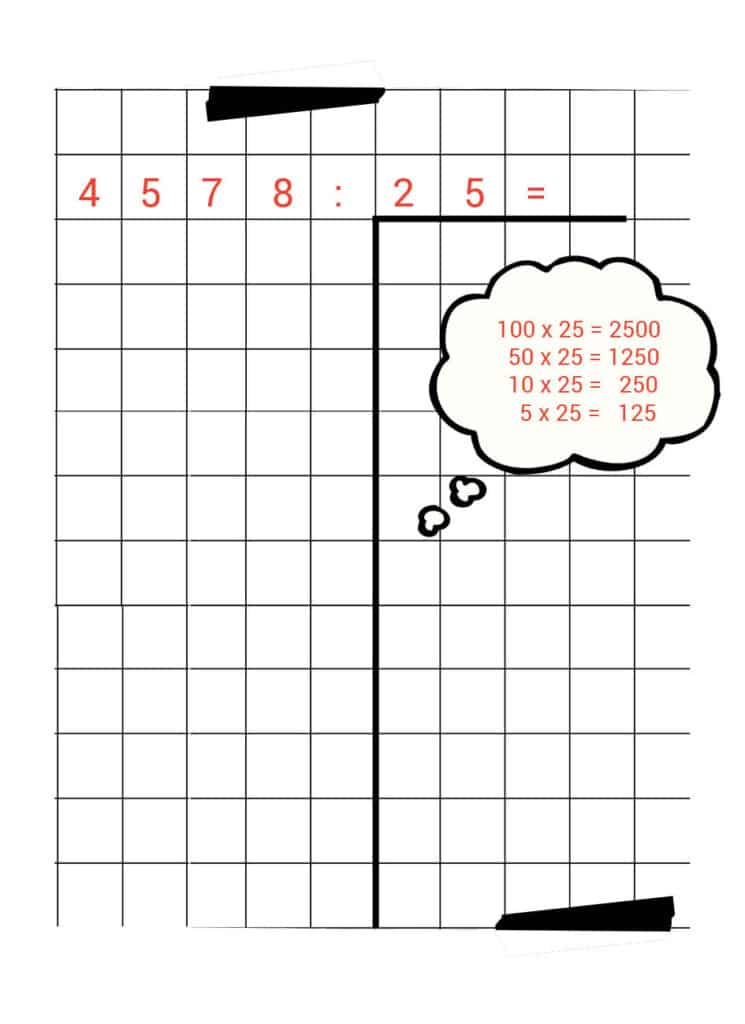
Oké, we zijn klaar om te beginnen. Jij ook?

Onthoud goed dat wij misschien andere happen nemen dan jij. Dat is helemaal niet erg. Je kunt onze uitwerking gebruiken om te controleren of je de som goed hebt uitgerekend. De uitkomst is als het goed is namelijk hetzelfde.

We willen dus weten hoe vaak 25 in 4.578 past.

Eerst doen we 100 x. Dat is een simpele stap, omdat hij in ons geheugensteuntje staat.

100 x 25 = 2500

We maken de minsom en houden 2.078 over.

We kijken nog eens naar ons geheugensteuntje en zien dat 25 nog 50 keer in de 2.078 past. Dat schrijven we op.

2.078 – 1.250 = 828

Ons schema ziet er ondertussen zo uit:

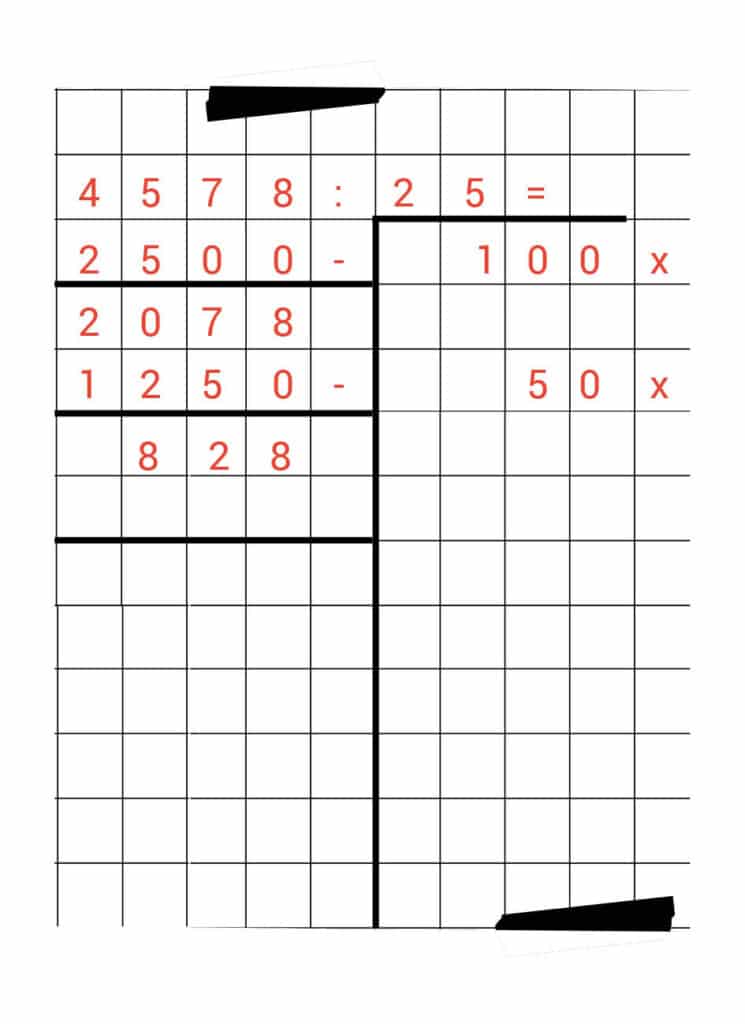
Voor onze volgende stap kijken we nog eens in ons geheugensteuntje. Daar zien we dat 10 x 25 hetzelfde is als 250.

Dat betekent dat 30 x 25 hetzelfde is als 750! Kijk, deze flinke hap kunnen we er in 1 keer vanaf halen.

828 – 750 = 78.

Vergeet weer niet ’30 x’ in de rechterkolom te schrijven.

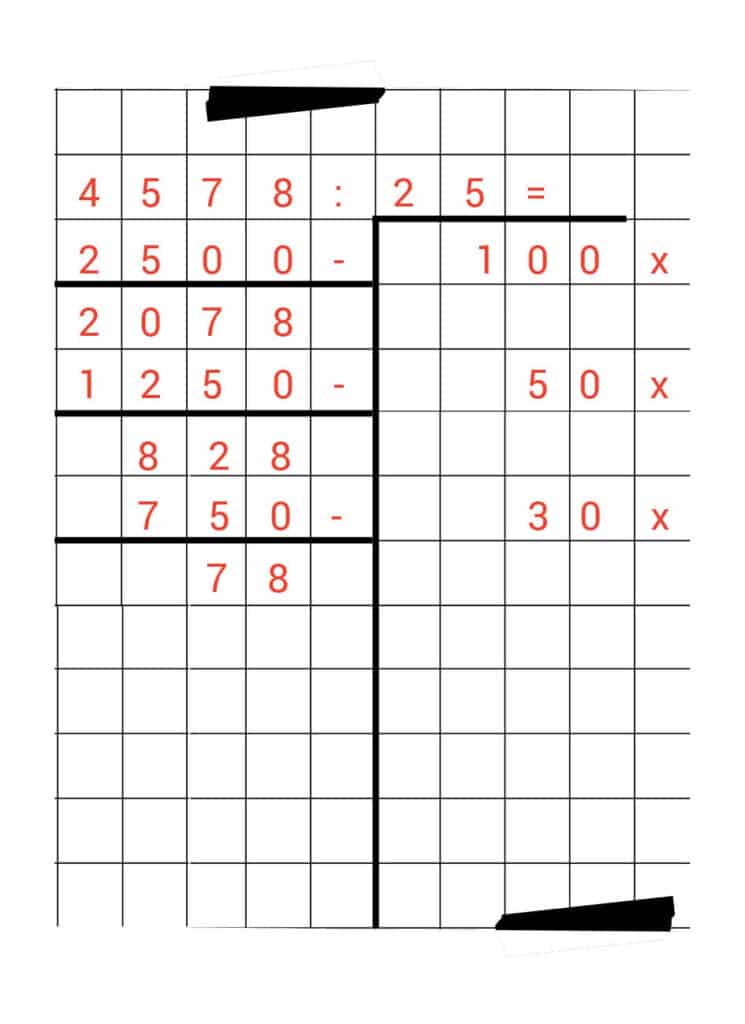
Het getal 25 past sowieso nog 3 x in 78. 3 x 25 is namelijk hetzelfde als 75. Deze stap zetten we ook nog in ons schema.

Kijk, zo:

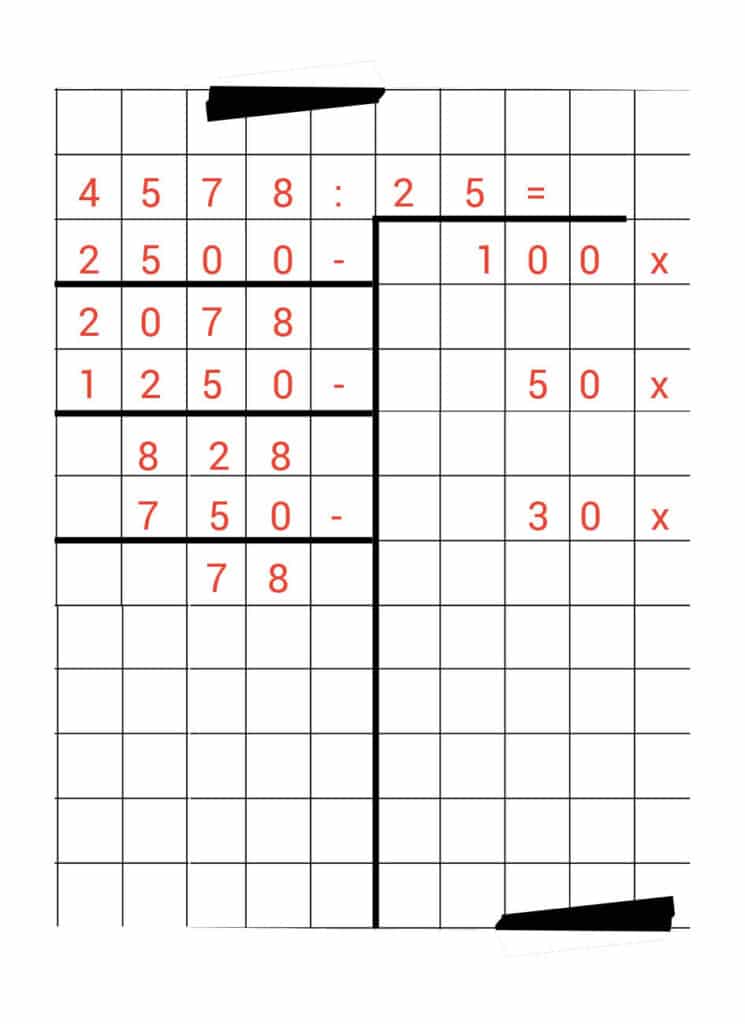
78 – 75 = 3

Ai, nu wordt het lastig. Het getal 25 past namelijk niet meer in 3. Dat betekent dat je die 3 over hebt, dat je die niet meer kunt gebruiken.

Dit overgebleven getal noem je ‘rest’.

En als je een som met ‘rest’ hebt, dan schrijf je alles wat overblijft nog achter het antwoord van de som.

Maar eerst tellen we de rechterkant bij elkaar op.

100 + 50 + 30 + 3 = 183

En dan blijven er nog 3 over. 

Schrijf nu de 3 achter het antwoord: 183 rest 3.

Je mag het woord ‘rest’ ook afkorten met de letter ‘r’.

4.578 : 25 = 183 r3

“Het aantal dat je aan het eind van de som niet meer kunt gebruiken, noem je ‘rest’ en schrijf je op achter het antwoord van de som.”

Delen onder elkaar

Rekenen met de hapmethode is een onderdeel van kolomsgewijs rekenen. Kolomsgewijs rekenen lijkt een beetje op cijferend rekenen (link naar artikel over cijferend rekenen, als dat er is). Dat is de categorie waar bijvoorbeeld de staartdeling onder valt.

Bij beide methodes werk je een rekensom met grote getallen stap voor stap, onder elkaar, uit.

Je kunt kolomsgewijs delen en cijferend delen daarom ook een andere naam geven, namelijk ‘delen onder elkaar’.

De hapmethode leer je door te oefenen

Je hebt in dit artikel een aantal voorbeelden gezien van deelsommen. Al die sommen hebben we uitgerekend met behulp van de hapmethode.

Samengevat heb je de volgende dingen geleerd:

• hoe je een deelsom met behulp van de hapmethode uitrekent;
• hoe je een deelsom met een deler groter dan 10 uitrekent met de hapmethode;
• hoe je een deelsom met rest uitrekenen met de hapmethode;
• wat ‘kolomsgewijs delen’ betekent.

En weet je… hoe meer je oefent met de hapmethode, hoe beter het gaat! Daarom hebben we hieronder nog 2 werkbladen staan, waarmee je flink aan de slag kunt.

Laat je het ons even weten als je vragen hebt over de hapmethode? Natuurlijk willen we ook graag weten wat jij de fijnste manier vindt om moeilijke deelsommen uit te rekenen.

We kijken uit naar je reactie!

Hapmethode werkblad

Werk de sommen op dit werkblad uit met behulp van de hapmethode. Schrijf alle tussenstappen op. Een voorbeeld van de uitwerking vind je onderaan de pagina. Hoewel de tussenstappen anders kunnen zijn dan die van jou, zou het antwoord hetzelfde moeten zijn.

1. 1. 665 : 19 =
2. 2. 3.515 : 95 =
3. 3. 344 : 8 =
4. 4. 392 : 14 =
5. 5. 5.823 : 20 =
6. 6. 3.842 : 26 =
7. 7. 694 : 12 =
8. 8. 732 : 15 =

Kolomsgewijs delen werkblad

Werk de sommen op dit werkblad uit met behulp van kolomsgewijs delen (ofwel: de hapmethode). Schrijf alle tussenstappen op.

1. 1. 1.643 : 35 =
2. 2. 2.784 : 32 =
3. 3. 2.665 : 65 =
4. 4. 4.925 : 23 =
5. 5. 1.385 : 8 =
6. 6. 7.349 : 19 =
7. 7. 9.366 : 20 =
8. 8. 3.152 : 32 =

Antwoorden hapmethode werkblad

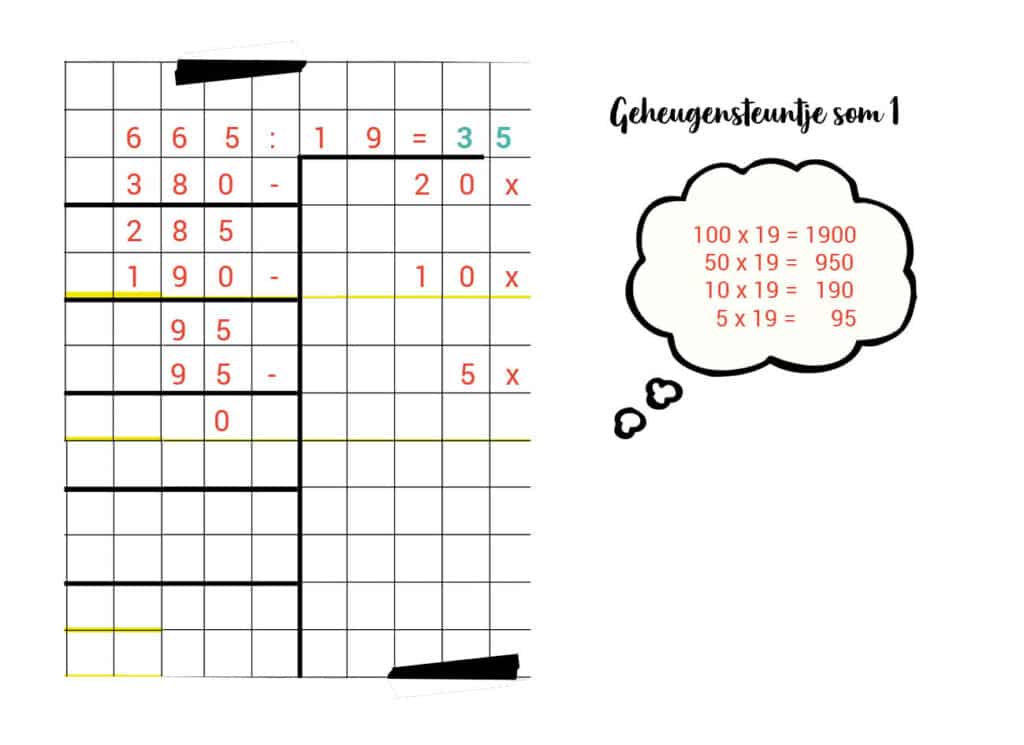
1. 665 : 19 = 35

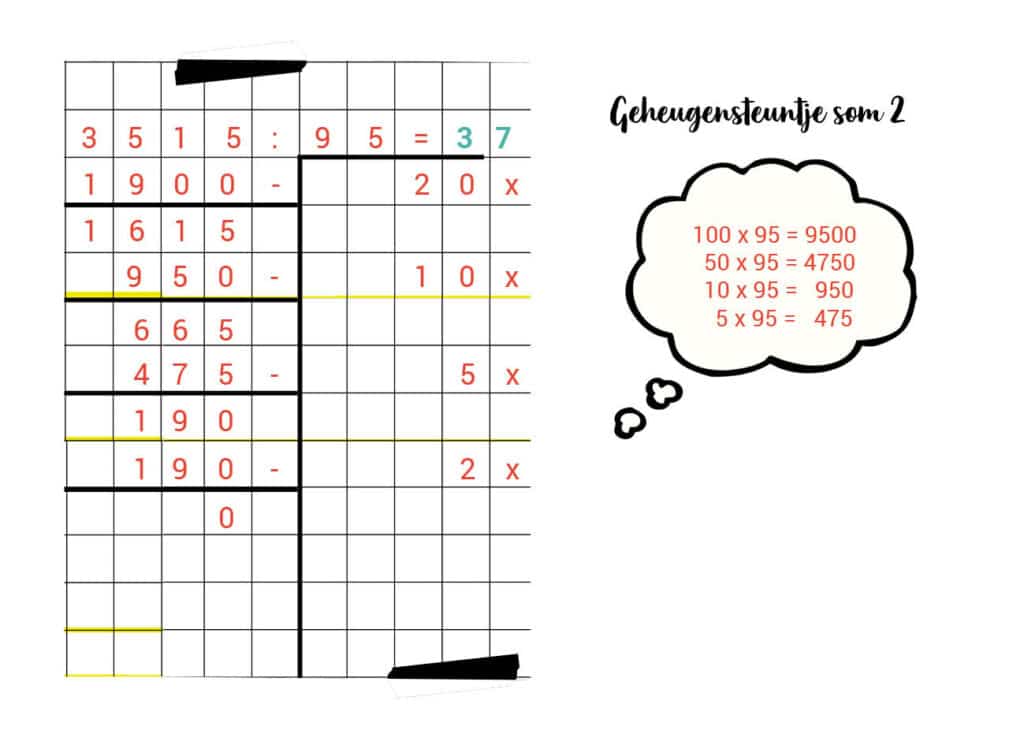
2. 3.515 : 95 = 37

3. 344 : 8 = 43

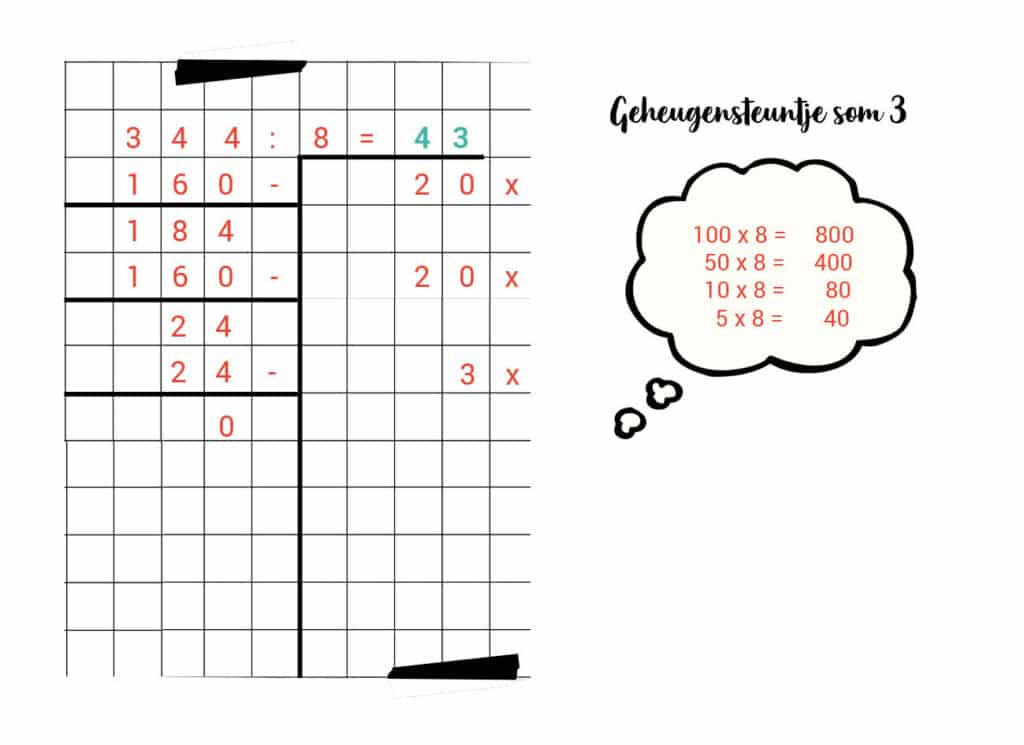
4. 392 : 14 = 28

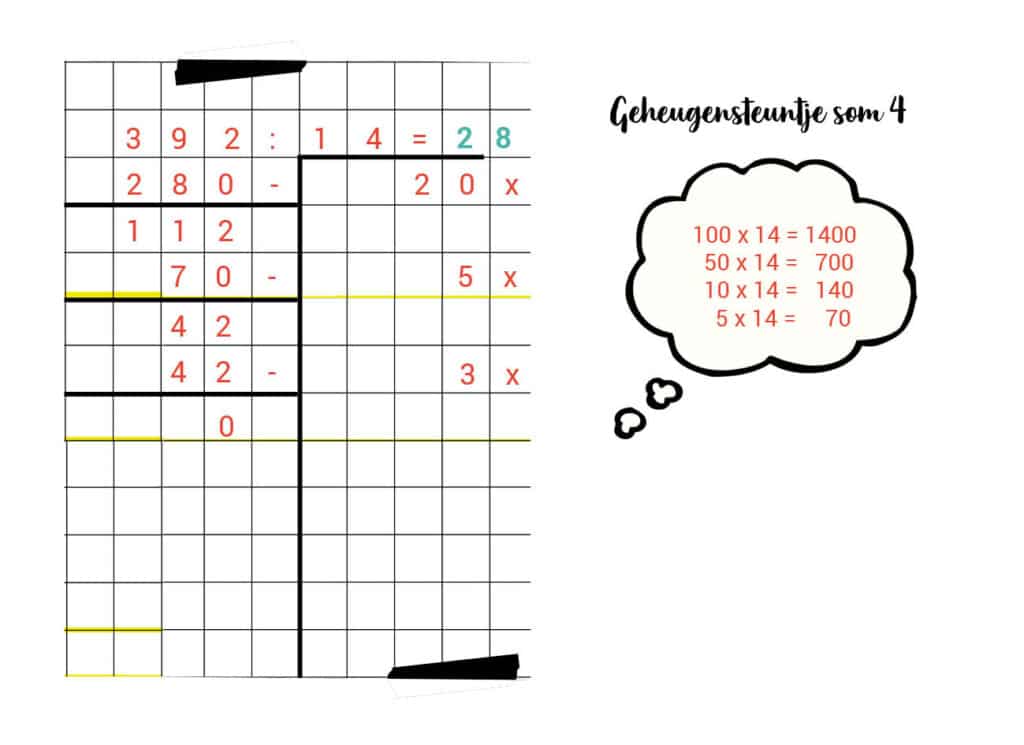
5. 5.823 : 20 = 291 r3

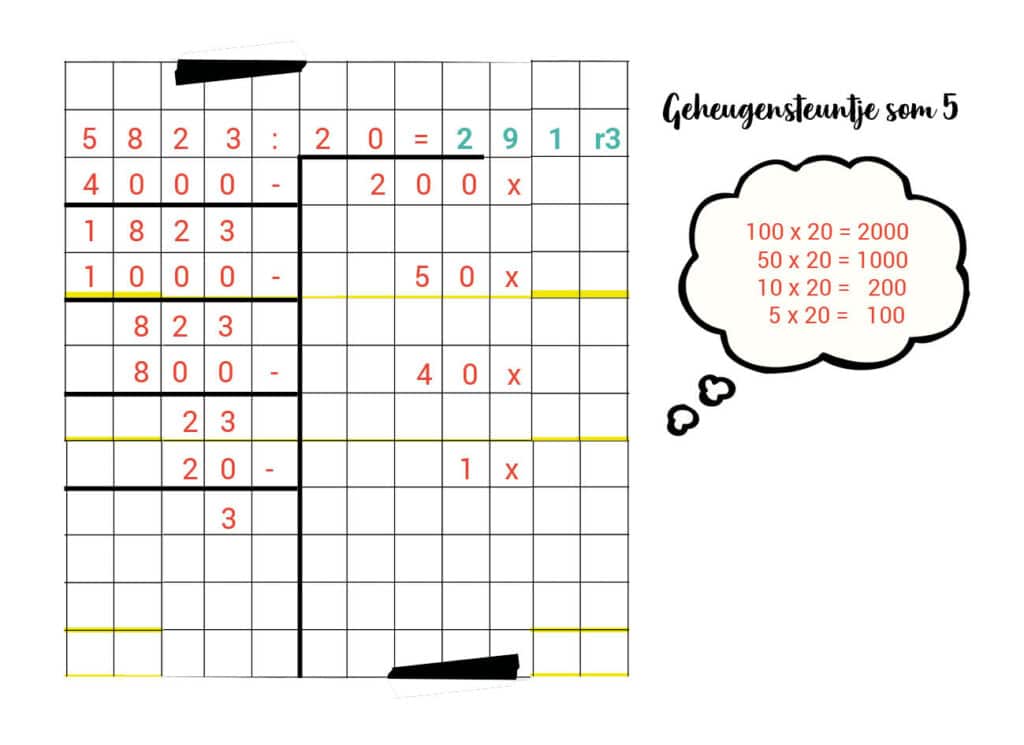
6. 3.842 : 26 = 147 r20

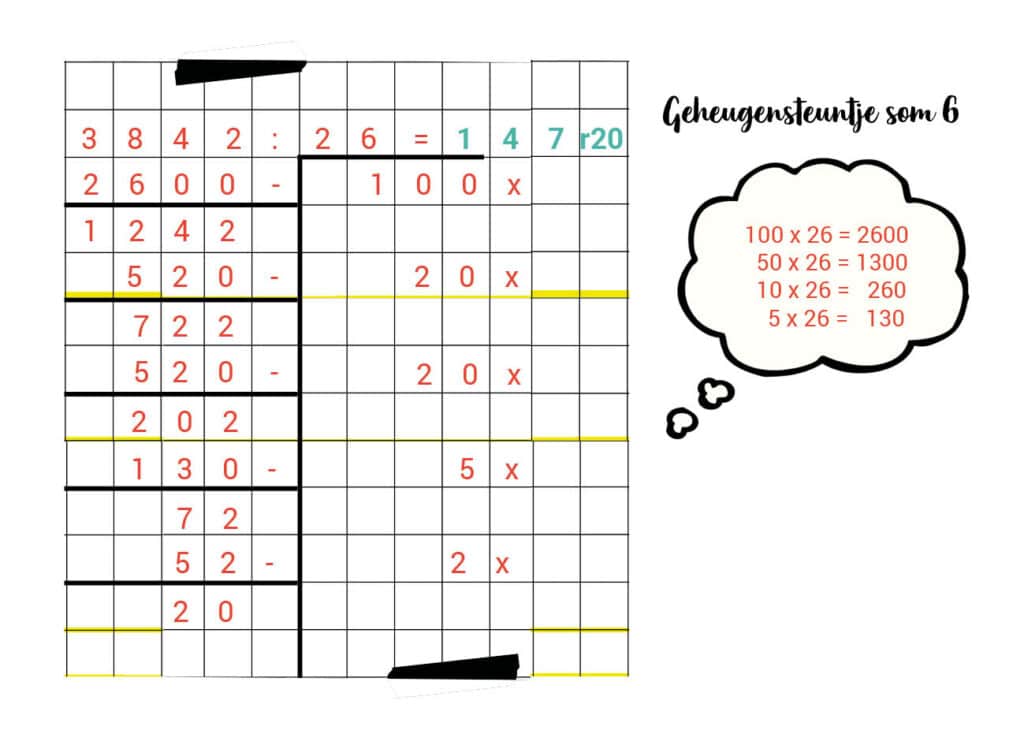
7. 694 : 12 = 57 r 10

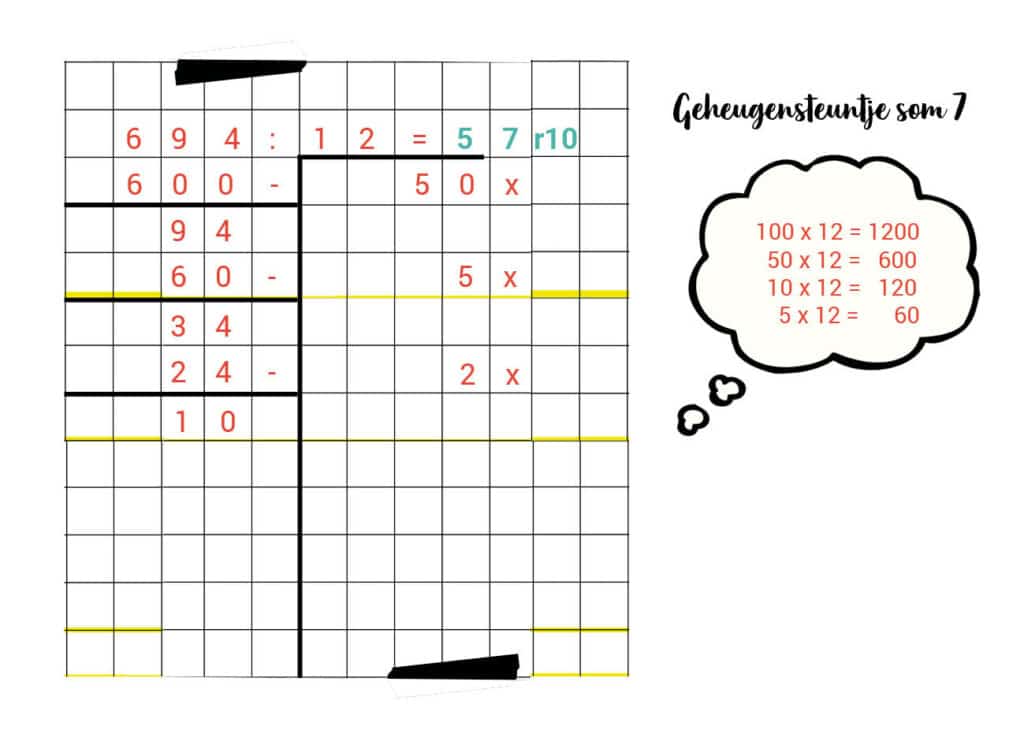
8. 732 : 15 = 48 r 12

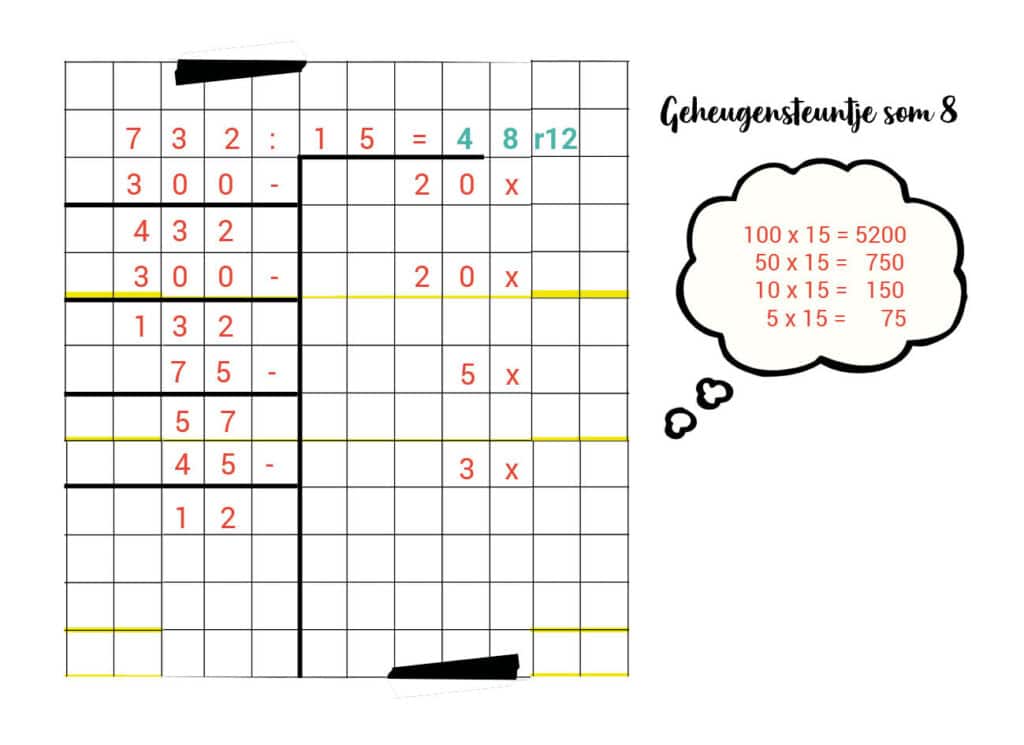
Antwoorden kolomsgewijs delen werkblad

1. 1. 1.643 : 35 = 47
2. 2. 2.784 : 32 = 87
3. 3. 2.665 : 65 = 41
4. 4. 4.925 : 23 = 214 r3
5. 5. 1.385 : 8 = 173 r1
6. 6. 7.349 : 19 = 386 r15
7. 7. 9.366 : 20 = 468 r6
8. 8. 3.152 : 32 = 98 r16

Noor Peels

Over Noor