Kolomsgewijs vermenigvuldigen: uitleg en oefenen

In dit artikel vertellen we je hoe je op de kolomsgewijze manier keersommen uitrekent: het kolomsgewijs rekenen. We geven je uitleg over kolomsgewijs vermenigvuldigen en voorbeelden, zodat jij jouw kind weer verder kunt helpen met rekenen oefenen.

Ook geven we je informatie over het vermenigvuldigen met tabellen. En als laatste laten we je zien hoe je getallen onder elkaar vermenigvuldigt. Dit wordt ook wel cijferend vermenigvuldigen genoemd.

In het kort weet jij dus straks:

• hoe je op een kolomsgewijze manier een keersom uitrekent;
• hoe je vermenigvuldigt met behulp van een tabel;
• en hoe je getallen onder elkaar vermenigvuldigt.

Na de uitleg volgen nog wat oefenopgaven, zodat je zelf lekker aan de slag kunt met je kind.

Bekijk ook:

• Kolomsgewijs rekenen
• Kolomsgewijs optellen
• Kolomsgewijs aftrekken
• Kolomsgewijs delen
• Cijferend vermenigvuldigen
• Keersommen oefenen
• Kommagetallen vermenigvuldigen
• Breuken vermenigvuldigen

Wat is kolomsgewijs vermenigvuldigen?

Kolomsgewijs rekenen betekent dat je met kolommen rekent.
Er zijn een heleboel verschillende manieren om keersommen uit te rekenen. En één manier is die met kolommen. Dit noemen we kolomsgewijs vermenigvuldigen. De beste manier om uit te leggen hoe kolomsgewijs vermenigvuldigen werkt, is door het je met voorbeelden te laten zien.

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

Voorbeelden van kolomsgewijs vermenigvuldigen

Voor het eerste voorbeeld gebruiken we deze keersom:

63 x 34 =

Deze som kun je uitrekenen met behulp van kolommen. Daarvoor teken je eerst de kolommen.
De getallen die erin komen hebben een vast plekje in de kolommen. De laatste kolom, de rechterkolom, is altijd bestemd voor de eenheden (E).
De kolom links ernaast is voor de tientallen (T).
Daarnaast komt de kolom voor de honderdtallen (H) en als laatste schrijf je de duizendtallen (D) op. De kolommen zien er nu dus zo uit:

Als je met nog grotere getallen zou werken, dan komen links van de duizendtallen nog de tienduizendtallen, honderdtallen, enzovoorts. Voor de sommen in dit artikel is het genoeg om bij de duizendtallen te stoppen.
Nu je de kolommen hebt getekend en de letters erboven hebt gezet, is het tijd om de getallen van onze som in te vullen: 63 en 34.

Het is heel belangrijk dat je de getallen uit de som op de juiste plek in de kolommen zet. Let op: het grootste getal staat altijd bovenaan.

Zet de 3 van 63 bovenaan in de kolom van de eenheden. De 6 komt daar links naast, bovenaan bij de tientallen. Het getal 34 plaats je daar netjes onder, met de 4 in de kolom van de eenheden en de 3 in die van de tientallen.
Daarna zet je een streep onder de som en vul je het x-teken in. Zo weet je altijd dat je deze getallen moet vermenigvuldigen.

Zo, de som staat klaar. We kunnen nu beginnen met de berekening.
Bij het kolomsgewijs vermenigvuldigen begin je altijd aan de linkerkant en onderaan. Dat is dus anders dan bij plus- en minsommen! Daar begin je namelijk bovenaan.
Als we links en onder beginnen, zien we als eerste een 3 staan bij de tientallen. Die 3 is 30 waard, omdat hij bij de tientallen staat.
Vermenigvuldig eerst 30 met het getal erboven. Dat is een 6, en die is 60 waard.
Je krijgt dan deze som: 30 x 60 =

Het is slim om deze som even helemaal links, naast de kolommen, op te schrijven. Dat hoef je niet altijd te doen, maar voor nu geven alle stappen een goed overzicht van wat je precies doet.

30 x 60 = 1800. Die uitkomst zet je in het kolommenschema, net onder de streep. Let erop dat je de getallen in de juiste kolommen zet:

Nu gaan we verder met de som. De volgende stap is 30 x 3.
30 x 3 = 90. Die vul je onder de 1800, in de juiste kolommen, in. Afbeelding:
Je hebt nu het eerste getal, 30, met alles dat erboven staat vermenigvuldigd. Daarmee ben je natuurlijk nog niet klaar. Er staat immers ook nog een 4 in de som. Die vermenigvuldig je ook met alles dat erboven staat.
Eerst doe je 4 x 60. Dat is 240. Die vul je in onder de 90.

Tot slot bereken je nog 4 x 3. Daarvan is de uitkomst 12.

Je hebt nu 4 uitkomsten, onder elkaar, in de kolommen staan. Deze 4 antwoorden moet je nog bij elkaar optellen om bij het antwoord van de som te komen. Zet daarvoor een streep en een +-teken onder de getallen neer. De kolommen maak je ook wat langer, zodat je weer wat meer schrijfruimte hebt. Kijk, zo:

Als je gaat optellen met kolommen begin je links en bovenaan. Eerst zoek je alle duizendtallen. Die tel je bij elkaar op.
In deze som zit maar 1 duizendtal. Schrijf onder de streep dus 1000 op.
Nu ga je verder met de honderdtallen. Je ziet 8 honderdtallen en 2 honderdtallen. Die tel je bij elkaar op. Samen zijn dat 10 honderdtallen. 10 honderdtallen zijn samen ook 1000. Schrijf de 1000 ook op.
Vervolgens tel je de tientallen bij elkaar op. In die kolom zie je 9 + 4 + 1. Dat zijn 14 tientallen; 140 dus. Ook dit getal schrijf je op.

Tot slot tel je alle eenheden bij elkaar op. Dat zijn er 2.
Zet onder al deze getallen weer een streep, met daarbij een +-teken. Je kolommenschema ziet er nu zo uit:

Je hoeft nu alleen nog maar alle getallen bij elkaar op te tellen. De uitkomst van deze som is 2.142.

Nu heb je zonder rekenmachine de moeilijke keersom 63 x 34 uitgerekend!
63 x 34 = 2.142

Nog een voorbeeldsom

We gaan dit nog eens oefenen. Dit keer doen we dat met deze som: 36 x 12 =
We gebruiken voor deze moeilijke som nogmaals het kolommenschema. Je hoeft het niet zo precies uit te tekenen als de vorige keer. Als je dat makkelijker vindt, mag dat natuurlijk wel.
Zet het hoogste getal bovenaan; dat is 36. Daar recht onder zet je netjes 12 neer.

Het is trouwens handig om ruitjespapier te gebruiken, want dan kan je alles netjes onder elkaar zetten. Zorg dus dat je genoeg ruitjespapier bij de hand hebt, als je deze sommen maakt.
Zet een streep onder de som en het x-teken ernaast. Daarna ben je klaar om te beginnen!

Let op: je begint weer links onderaan met je som. Daar zie je 1 tiental, 10 dus.

Vermenigvuldig die 10 met de 30 erboven.
10 x 30 = 300
Vul de 300 in, netjes in de hokjes onder de streep. Let erop dat je de honderdtallen, tientallen en eenheden in de juiste kolommen zet.
Vervolgens vermenigvuldig je dezelfde 10 met de 6 van 36. 10 x 6 = 60.
Dit getal vul je ook in.

Je hebt nu alle sommen gemaakt met de 10. Dat betekent dat je verder kunt gaan met de 2.
De 2 staat bij de eenheden, dus die is ook echt 2 waard.

Eerst doe je 2 x 30. Dat is 60.
En dan nog 2 x 6. Daar komt 12 uit. Zet al deze getallen weer netjes onder elkaar in de juiste hokjes. Zet er ook meteen een streep en een + onder, zodat je weet wat de volgende stap is.

Eerst ga je op zoek naar de honderdtallen, dat zijn er 3. Schrijf daarom 300 op onder de streep.
Vervolgens zoek je alle tientallen. Dat levert de volgende som op:
6 + 6 + 1 = 13
13 tientallen zijn hetzelfde als 130. Dit getal zet je onder de 300.
Daaronder volgt nog de 2, want je hebt 2 eenheden. Als je vervolgens alles bij elkaar optelt, kom je uit op 432.

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

We zien nu de uitkomst van onze oorspronkelijke som.

36 x 12 = 432
Zie je hoe makkelijk je zo’n moeilijke som kunt uitrekenen als je kolommen gebruikt?

Vermenigvuldigen met een tabel

We hebben je nu laten zien hoe je keersommen met behulp van kolommen uitrekent. Je kunt keersommen ook uitrekenen met behulp van een tabel. Die manier laten we je nu zien.
Weet je nog dat we de video begonnen met de som 63 x 34? Diezelfde som gaan we nu nog eens uitrekenen, maar dan met een tabel.
Eerst teken je de tabel. Linksboven zet je nu het keerteken neer, zodat je weet dat je met vermenigvuldigen bezig bent. Dan ziet het er zo uit:

Daarna zet je het hoogste getal bovenin de tabel. Dat is 63. Haal de tientallen en de eenheden uit elkaar. Schrijf eerst 60 op en daarnaast de 3. Aan het einde zet je nog een keer 63 neer, want daar komt alles bij elkaar.

Dan het tweede getal, 34. Ook dit getal haal je uit elkaar. Dan krijg je 30 en 4. Schrijf de 30 links in de tabel en de 4 eronder. Helemaal onderaan komt weer het getal in zijn geheel: 34.

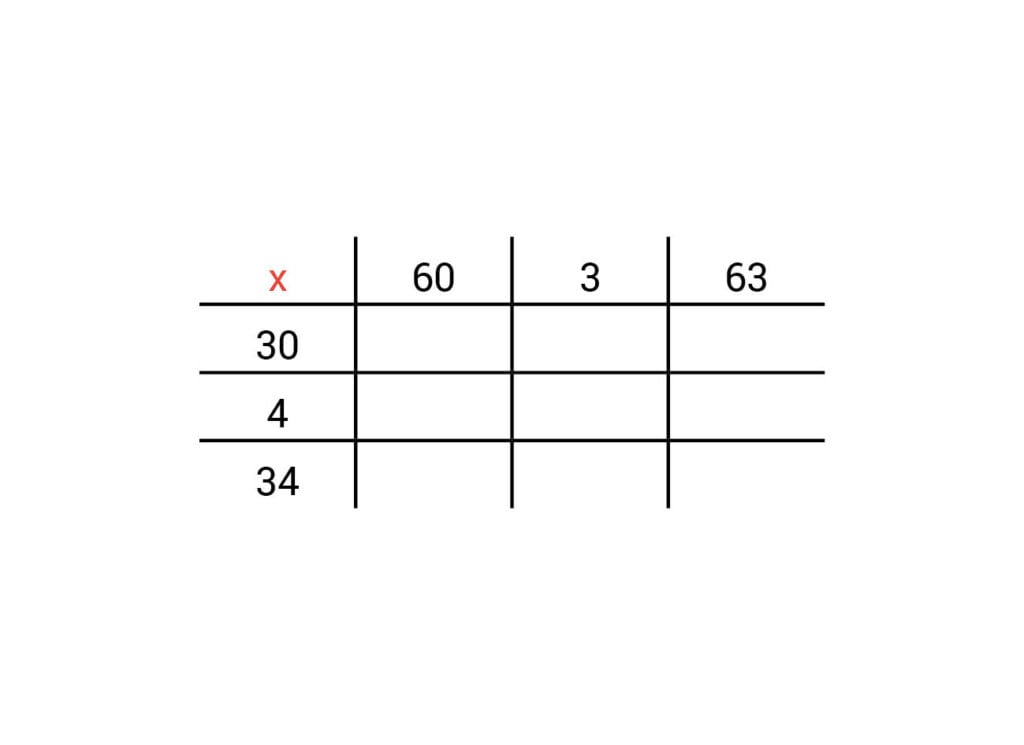
Nu ga je alle vakjes uitrekenen.
Je begint bij 30 x 60. Dat is 1800. Deze uitkomst komt in het eerste hokje. Kijk, zo:

Dan doe je hetzelfde bij de andere keersommen.
30 x 3 = 90 4 x 60 = 240 4 x 3 = 12
Zet deze getallen in de juiste vakjes.

Je hebt nu alle losse sommen uitgerekend. In de volgende stap ga je al die getallen bij elkaar optellen.
In de bovenste rij staan de getallen 1800 en 90. Die tel je bij elkaar op. Dan kom je op 1890 uit. Schrijf dat getal onder de 63. 1890 is meteen het antwoord van de som 30 x 63.
Nu gaan we naar de volgende rij.
Daar staan de getallen 240 en 12. Dat is samen 252. Zet die onder het getal 1890. 252 is ook meteen de uitkomst van de som 4 x 63.

Wat je nu van links naar rechts hebt gedaan, kun je ook doen met de getallen van boven naar beneden. We beginnen daarvoor links in de tabel.
1800 + 240 = 2040
Dat is meteen de uitkomst van 34 x 60.
Daarnaast zie je nog de som 90 + 12. Dat is 102.
En je raadt het al: 102 is ook de uitkomst van 34 x 3.

Je hebt nu bijna de hele tabel ingevuld. Met deze uitkomsten kun je het antwoord op de som vinden.
Zoals je ziet, is het vakje bij de som 34 x 63 nog leeg. Maar het antwoord is best makkelijk te vinden.

Je kunt kiezen uit 2 manieren:

• Tel de getallen boven dit lege vakje bij elkaar op.
• Tel de getallen naast het lege vakje bij elkaar op.

2040 + 102 = 2142 1890 + 252 = 2142
Zie je dat? Beide sommen hebben dezelfde uitkomst!
Je weet nu ook de uitkomst van de keersom 63 x 34. Dat is ook 2140!

Onder elkaar vermenigvuldigen

Je weet nu dat je een keersom kunt uitrekenen met een kolom én met een tabel. Het zal je misschien verbazen, maar er is nóg een manier die je kunt gebruiken.
Deze manier heet vermenigvuldigen onder elkaar of cijferend vermenigvuldigen.
Laten we met een makkelijke som beginnen: 2 x 13 =
Deze som kun je misschien ook wel uit je hoofd uitrekenen. En dat is handig, want dan kun je straks controleren of je het cijferend vermenigvuldigen ook echt goed snapt.

Eerst zet je de som netjes onder elkaar. Net als bij kolomsgewijs vermenigvuldigen zet je de eenheden altijd onder elkaar, en daarna de tientallen, de honderdtallen, enzovoorts. Gebruik weer ruitjespapier als je dat hebt.
We doe dat eens voor deze som. Ook zetten we een streep onder de getallen en we plaatsen er een keerteken bij.

Nu begin je de berekening. Je start met het vermenigvuldigen van de eenheden:
2×3=6
Zet de 6 netjes in de kolom van de eenheden onder de streep:

Vervolgens vermenigvuldig je 2 met 1. Dat is natuurlijk 2. Die 2 zet je in de kolom van de tientallen. Dat doe je, omdat de 1 in het bovenste getal ook een tiental is. Die staat eigenlijk voor 10.
De 2 zet je vóór de 6 neer:

De uitkomst van de som 13 x 2 is dus 26!
Omdat deze som nog wel erg makkelijk was, gaan we nu een stapje verder. Dat doen we met deze som:
4 x 14 =
We schrijven de som weer op de goede manier op:

Zie je dat de eenheden weer netjes onder de eenheden staan?
We beginnen met de berekening van de eenheden:
4 x 4 = 16.
16 past alleen niet zo mooi in de kolom van de eenheden. Daarom schrijf je alleen de 6 op. De 1 breng je naar de buurman toe:

Vervolgens ga je verder: 4×1=4

Maar zoals je ziet, staat die extra 1 nog in deze kolom. Die tel je op bij de 4.
4+1=5
De 5 schrijf je op onder de streep, in de rij van de tientallen:

Nu weten we de uitkomst van de som:
4 x 14 = 56

Een beetje moeilijker

Als we de sommen wat moeilijker willen maken, pakken we gewoon 2 grote getallen.
Bijvoorbeeld deze som: 23 x 33 =
Let op: Het grootste getal moet bij deze rekenmethode altijd bovenaan staan. Bij deze som is dat dus 33.

Je begint, net als bij de vorige sommen, rechtsonder. Bij de 3 dus.
Eerst kijk je weer naar de eenheden. Daar krijg je 3 x 3. Dat is 9. Die vul je in.
Als je daarna naar de tientallen kijkt, krijg je weer 3 x 3. Die 9 schrijf je links naast de 1e 9 op.

We zijn nu nog niet klaar. De 2 is er namelijk ook nog in het onderste getal! Vergeet hierbij niet dat de 2 geen 2 is, maar 20.

Daarom zet je onder de 99 alvast een 0 in de volgende rij:

Vervolgens maak je weer alle berekeningen met de 2.
2 x 3 (die van de eenheden) = 6
Deze 6 plaats je direct naast de 0.
Nog een keer 2 x 3. Dat is natuurlijk weer 6. Die zet je links naast de 1e 6.

Je ziet dat onder deze 2 getallen ook al een streep met een +-teken staat. Dat doen we, omdat je deze 2 uitkomsten nog bij elkaar moet optellen.
Weet je nog hoe dat werkt? 9 + 0 is natuurlijk niet zo moeilijk. Dat is 9. Die schrijf je op in de kolom van de eenheden.
Maar als je nu 9 + 6 moet uitrekenen, krijg je 15, een getal van 2 cijfers dus! De 5 schrijf je op en de 1 onthoud je voor de volgende berekening.

Bij die laatste 6 tel je dus nog 1 op. Dat is 7. Deze 7 plaats je links naast de 5.

De uitkomst van deze lastige som ken je nu dus ook.
23 x 33 = 759
Laten we het nog 1 keer wat moeilijker maken met deze som:
36 x 47 =
Zet deze getallen weer onder elkaar, met het grootste getal bovenaan:

Als je nu begint met de eerste som, zie je dat die meteen een lastigheid geeft:
6 x 7 = 42

Er is alleen ruimte voor de 2; niet voor de 4. Breng daarom de 4 naar de buurman toe:

De volgende som is 6 x 4. Dat is natuurlijk 24. Maar nu moet je nog iets doen met de 4 die overgebleven is uit de eerste som. Deze 4 tel je bij 24 op. Dan krijg je 28.
28 schrijf je links van de 2 op.

Nu gaan we verder met de 3 van 36. Die staat immers ook nog in de som!
De 3 is eigenlijk 30, dus we schrijven alvast een 0 op onder 282. Daarna ga je verder:
3 x 7 = 21
De 1 schrijf je op, de 2 breng je naar de buurman.
3 x 4 = 12
Bij die 12 tel je nog de overgebleven 2 op. Dan wordt het 14.

Je ziet dat we onder deze getallen weer een streep en een plusteken hebben gezet. De 2 uitkomsten tel je weer bij elkaar op.
Dan kom je uit op 1692.
36 x 47 is dus 1692!

Vermenigvuldigen doe je op veel manieren

In dit artikel heb je gezien dat je keersommen op veel verschillende manieren kunt oplossen:

• met kolommen;
• met tabellen;
• door ze onder elkaar te zetten.

We hopen dat je na deze uitleg voortaan precies weet hoe de verschillende methodes werken.
Verder zijn we natuurlijk benieuwd naar jouw favoriete manier van keersommen uitrekenen. Voor welke van de 3 zou jij gaan als je mocht kiezen?
Wil je nog oefenen? Hieronder staan nog wat opgaven. Laat het ons gerust weten als je nog vragen hebt over kolomsgewijs vermenigvuldigen, keersommen met tabellen of keersommen onder elkaar.
Veel succes!

Kolomsgewijs vermenigvuldigen werkblad

Reken de volgende sommen uit door kolomsgewijs te vermenigvuldigen. Gebruik daarvoor ruitjespapier. De antwoorden vind je onderaan de pagina.

1. 1. 84×7=
2. 2. 9×23=
3. 3. 62×12=
4. 4. 42×29=
5. 5. 73×36=

Rekenen met tabellen werkblad

Reken de volgende sommen uit door gebruik te maken van tabellen. Gebruik daarvoor ruitjespapier. De antwoorden vind je onderaan de pagina.

1. 1. 74×2=
2. 2. 39×52=
3. 3. 95×12=
4. 4. 43×62=
5. 5. 28×45=

Werkblad onder elkaar vermenigvuldigen

Reken de volgende sommen uit door onder elkaar te vermenigvuldigen. Gebruik daarvoor ruitjespapier. De antwoorden vind je onderaan de pagina.

1. 1. 27×35=
2. 2. 63×82=
3. 3. 13×26=
4. 4. 48×93=
5. 5. 35×78=

Antwoorden werkblad kolomsgewijs vermenigvuldigen

1. 1. 84×7=588
2. 2. 9×23=207
3. 3. 62×12=744
4. 4. 42×29=1218
5. 5. 73×36=2628

Antwoorden werkblad vermenigvuldigen met tabellen

1. 1. 74×2=148
2. 2. 39×52=2028
3. 3. 95×12=1140
4. 4. 43×62=2666
5. 5. 28×45=1260

Antwoorden werkblad vermenigvuldigen onder elkaar

1. 1. 27×35=945
2. 2. 63×82=5166
3. 3. 13×26=338
4. 4. 48×93=4464
5. 5. 35×78=2730

Oefening Rekenen Groep 2 (Gratis)

Download

Oefenbladen Groep 3 Rekenen (Gratis)

Download

Oefenbladen Rekenen Groep 4 (Gratis)

Download

Oefenbladen Rekenen Groep 5 (Gratis)

Download

Oefenbladen Rekenen Groep 6 (Gratis)

Download

Oefenbladen Rekenen Groep 7 (Gratis)

Download

Oefenbladen Rekenen Groep 8 (Gratis)

Download

Rochelle Schaepkens, BEd Master EN

Rochelle behaalde een Bachelor en Master of Education (PABO en Master Leren en Innoveren). Daarnaast heeft ze de opleidingen tot Taalexpert, Rekenexpert en Remedial Teaching gevolgd. Ze heeft 20 jaar ervaring als leerkracht en unitleider op een basisschool. Nu werkt ze als docent op de Pabo en als Content Creator voor Wijzer over de basisschool.

Over Rochelle