Kommagetallen vermenigvuldigen, hoe doe je dat?


Je kind zit in groep acht en dan blijkt vermenigvuldigen met kommagetallen ineens een lastig onderdeel van het rekenen in groep 8 te zijn… Je wilt hulp bieden maar waar begin je?
Vraag eerst aan je kind of het onderstaande vaardigheden beheerst.
Een overzicht van de opbouw van de keersommen in de basisschool:
- Groep 4 – Je kind leert de keertafels 1 t/m 5 + 10 (de nieuwste rekenmethodes bieden in groep 4 de tafels 1 t/m 10 aan).
- Groep 5 – Keertafels 1 t/m 10 zijn aangeboden en het beantwoorden van de sommen moet een automatisme worden. Aan het eind van groep 5 wordt een begin gemaakt met het maken van tiental tafels (4 x 15 =).
- Groep 6 – Je kind gaat werken met honderdtal tafels (3 x 500 = ). De geldsommen komen daar ook bij. Dit is de kennismaking met kommagetallen vermenigvuldigen..
- Groep 7 – Vermenigvuldigen met 10, 100, 1.000. Cijferend vermenigvuldigen (ook) met geldbedragen.
- Groep 8 – (Cijferend) vermenigvuldigen met kommagetallen.
TIP voor alle groepen: blijf de keertafels, en vanaf groep 6 ook de deeltafels, oefenen en herhalen!
De Cito-toets vraagt van de kinderen een flexibele toepassing.

Mocht blijken dat de keertafels nog niet geautomatiseerd zijn, oefen dan dagelijks één tafel en dat voor bijvoorbeeld twee weken lang. Na twee weken oefen je een volgende keertafel.
Rekentermen bij vermenigvuldigen met kommagetallen
Ken je dat? Je gaat samen aan de slag met de rekenopdrachten die je kind van school heeft meegekregen en je loopt tegen rekentermen aan, waarvan je de betekenis eerst op moet zoeken voordat je aan je uitleg kunt beginnen…
Hier volgt een overzicht zodat je toch snel aan de slag kunt gaan. 😉
Rekentermen die je tegen kunt komen:
Keertafels
Alle tafels met het rekenteken X
7 x 3 = 21
3 x 11 = 33

Deeltafels
Alle tafels met het rekenteken :
21 : 7 = 3
33 : 11 = 3
Vermenigvuldigen (keer) (maal)
Je gebruikt het rekenteken X om de som uit te rekenen. Vermenigvuldigen wordt ook wel ‘keer’ of ‘maal’ genoemd.
X – Soms gebruikt men een punt, die een beetje hoger geplaatst wordt.
Delen

Je gebruikt het rekenteken : om de som uit te rekenen.
Soms staat er een horizontaal streepje tussen de 2 puntjes
of
een schuine streep.
Eenheden, tientallen, honderdtallen
In het getal 453 zijn er drie eenheden. In het getal 453 zijn er vijf tientallen. Het getal 453 heeft vier honderdtallen.
Cijferend vermenigvuldigen
De som uitrekenen door de getallen onder elkaar te plaatsen. Vergeet niet een 0 te plaatsen als je met de tientallen vermenigvuldigt 😉 (op deze manier werden ‘vroeger’ deze sommen ook uitgerekend).

De som uitrekenen door eerst de honderdtallen te vermenigvuldigen, dan de tientallen en vervolgens de eenheden. Voordeel: hoofdrekenen wordt makkelijker. Schattend rekenen wordt makkelijker. Nadeel: Bij grote getallen, krijgt je kind een lange uitwerking.

Handig vermenigvuldigen
Je leert je kind om de grote keer som te splitsen, uit te rekenen en bij elkaar op te tellen.

De kale som
De som geschreven met cijfers en het rekenteken, zonder het verhaal (de redactiesom).
Betekenisvolle situatie
Je laat de (kale) som zien met behulp van een, voor je kind, betekenisvolle situatie.
Wat je kind moet weten:
Links / rechts
Je kind moet weten wat links en rechts is. Alternatief: schrijf een R en een L op beide handen.
Keertafels
Je kind kent de keertafels voldoende. Alternatief = een tafelkaart.
Inzicht in hele getallen versus kommagetallen
Je kind kan van hele getallen, kommagetallen maken. Bijvoorbeeld 2, kun je ook schrijven als 2,0.
Keersommen met 10, 100 of 1000
Je kind weet dat bij keersommen met 10, 100 of 1000 de komma 1, 2 of 3 plaatsen naar rechts schuift. Keer = komma naar rechts. Delen = komma naar links.
Aan de slag met kommagetallen vermenigvuldigen
Stel, je kind heeft de opdracht om de volgende som op te lossen: 2,35 x 0,3
In onderstaand schema staat de strategie, dé manier, om dit soort sommen op te lossen.
De strategie bij kommagetallen vermenigvuldigen

Waarom deze strategie? Omdat deze manier geen verwarring geeft zodra er gewerkt moet worden met 3 of 4 getallen achter de komma of met getallen waarbij het aantal cijfers achter de komma niet gelijk is.
Welke soorten sommen met kommagetallen kennen we (in groep 8)
- Kommagetallen vermenigvuldigen met 10, 100, 1000 enzovoort.
- Kommagetallen vermenigvuldigen met een heel getal.
- Kommagetallen vermenigvuldigen met een kommagetal.
- Kommagetallen vermenigvuldigen met een kommagetal dat kleiner dan 1 is.
- Kommagetallen kleiner dan 1 vermenigvuldigen met kommagetallen kleiner dan 1.
1. Kommagetallen vermenigvuldigen met 10, 100, 1000
Bij de sommen waarbij het kommagetal vermenigvuldigd mag worden met 10, gaat de komma 1 plaats naar rechts.
10 x 0,5 = 5 en is omgekeerd natuurlijk het zelfde antwoord: 0,5 x 10 = 5.
Voorbeeld:
10 x 2,89 = 28,9
59,45 x 10 = 594,5
Bij de sommen waarbij het kommagetal vermenigvuldigd mag worden met 100, gaat de komma 2 plaatsen naar rechts.
100 x 0,349 = 034,9 = 34,9. Ook omgekeerd is dit hetzelfde antwoord: 0,349 x 100 = 34,9.
Voorbeeld:
1,591 x 100 = 159,1
Mocht het getal, dat vermenigvuldigd mag worden, te weinig cijfers hebben om de komma te verplaatsen weet dan dat je er nullen achter mag schrijven om toch de komma het juiste aantal plaatsen te kunnen verschuiven.
1,2 x 100 = ?
Je kunt dan schrijven: 1,2000 x 100 = 120,00 = 120
Als je het antwoord hebt uitgerekend dan mag je de nullen voor in het getal maar ook de nullen achteraan (na de komma) in het antwoord weglaten. Dat ziet er zo uit:
0,6000 x 100 = 060,00 = 60
Ditzelfde geldt voor x 1000 (en alle andere getallen met een één en verder alleen maar nullen). Dus, keer 1000, dan gaat de komma drie plaatsen naar rechts.
Voorbeeld:
1,5282 x 1000 = 1528,2
0, 68 x 1000 = 0,6800 x 1000 = 0680,0 = 680
Vermenigvuldigen met bijvoorbeeld 100.000? Dan gaat de komma 5 plaatsen naar rechts.
Voorbeeld:
1,5 x 100.000 = 150000
2. Kommagetallen vermenigvuldigen met een heel getal
Bij kommagetallen vermenigvuldigen met een heel getal, kun je de eerder genoemde strategie inzetten.
Schrijf de cijfers op zonder de komma en bereken de som volgens ‘cijferend rekenen’. Of; schrijf de cijfers op met de komma, maar doe, tijdens het uitrekenen, alsof de komma er niet is.
Er komt 1 cijfer achter de komma, want in de getallen die je vermenigvuldigd hebt, stond in totaal ook 1 cijfer achter de komma.
3. Kommagetallen vermenigvuldigen met een kommagetal
Hier verandert er niets in vergelijking met de sommen genoemd bij punt 2. Ook hier schrijf je de cijfers op met (of zonder) de komma maar doe, tijdens het uitrekenen, net alsof de komma er niet is.
In het onderstaande voorbeeld zie je twee getallen met in totaal vier cijfers achter de komma:
Voorbeeld:
45,89 x 2,34 =
Zet de cijfers weer onder elkaar (cijferend vermenigvuldigen)

Ook in het antwoord in totaal vier cijfers achter de komma.
Nog een voorbeeld:
392,5 x 1,3 =
Zet de cijfers weer onder elkaar (cijferend vermenigvuldigen)
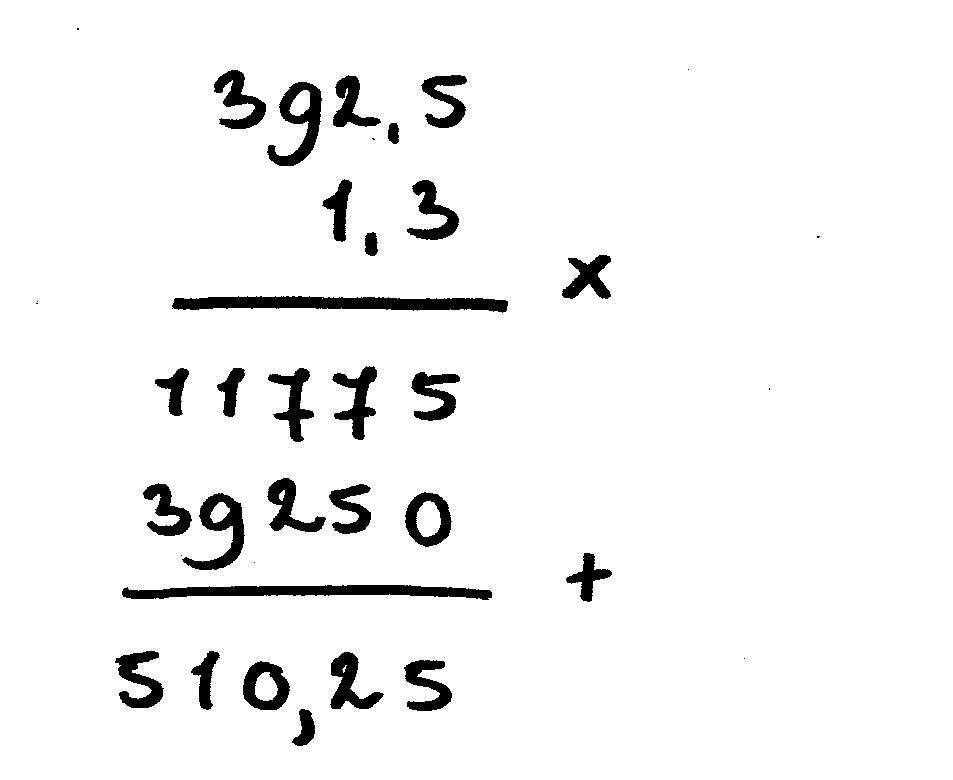
Ook in het antwoord in totaal twee cijfers achter de komma.

4. Kommagetallen vermenigvuldigen met een kommagetal dat kleiner is dan 1
De kommagetallen die kleiner zijn dan 1, dus de getallen met een 0…., mag je tijdens het vermenigvuldigen zonder 0 schrijven. Of, als je dat handiger vindt, de som met 0 opschrijven maar deze 0 niet vermenigvuldigen. Dat kan omdat alle uitkomsten van sommen x 0 als antwoord 0 hebben. Ook mag je de getallen zo onder elkaar schrijven dat het makkelijk is om het uit te rekenen. Er is dus geen vaste volgorde!
Voorbeeld:
0,14 x 5,28 mag je als volgt opschrijven en uitrekenen als een gewone (grote) keer som:

De getallen die we vermenigvuldigd hebben, hebben in totaal 4 cijfers achter de komma. Dat moet dus in het antwoord óók!
Het antwoord wordt dus:

Je ziet: je mag het getal aanvullen met nullen zodat je het juiste aantal cijfers achter de komma kunt zetten.
Nog een voorbeeld:
6,34 x 0,04 =
mag je als volgt opschrijven en uitrekenen als een gewone (grote) keer som:

De getallen die we vermenigvuldigd hebben, hebben in totaal 4 cijfers achter de komma. Dat moet dus in het antwoord óók!
Het antwoord wordt dus:

Opnieuw kun je zien dat je het getal mag aanvullen met nullen zodat je het juiste aantal cijfers achter de komma kunt zetten.
5. Kommagetallen kleiner dan 1 vermenigvuldigen met kommagetallen kleiner dan 1
Kommagetallen kleiner dan 1 zijn te herkennen aan de 0 voor de komma. De nullen voorin de getallen mag je weg laten of, als je dat overzichtelijker vindt, wel opschrijven maar niet uitrekenen, keersommen met 0 zijn immers altijd 0.
Een voorbeeld:
0,6 x 0,06 =
Zet de cijfers weer onder elkaar (cijferend vermenigvuldigen)

Ook in het antwoord in totaal drie cijfers achter de komma. Het antwoord is dus:

Ik had ook kunnen schrijven, of als je er een beetje handigheid in krijgt, kunnen zien:
Dat 6 x 6 = 36
Dan tel ik de cijfers die achter de komma staan. Dat zijn er in deze som in totaal drie, dus ook drie cijfers achter de komma in het antwoord.
Je mag de uitkomst aanvullen met nullen totdat je het juiste aantal cijfers achter de komma kunt zetten.
6 x 6 = 36, in de uitkomst moeten er drie getallen achter de komma gezet worden; het juiste antwoord is dan 0,036.
Nog een voorbeeld:
0,15 x 0,0 43 =
Deze som kan ik niet makkelijk uit mijn hoofd uitrekenen, dus ik schrijf de som als volgt op:

Omdat in de keer som in totaal vijf cijfers achter de komma staan, schrijf ik ook in het antwoord vijf cijfers achter de komma:
Het goede antwoord is dan:

Nog een voorbeeld:
0,04 x 0,0012 =
Deze som (4 x 12) weet ik uit mijn hoofd, dat is namelijk 48.
Ik zie dat beide getallen in totaal zes cijfers achter de komma hebben.
Mijn antwoord wordt dus: 0,000048
Geldsommen met vermenigvuldigen
Sommen met geldbedragen zijn ook kommagetallen en kun je op dezelfde manier uitrekenen!


Let wel op dat je het geldteken voor het getal zet. Dus als je in Nederland woont wordt het juiste antwoord € 7,00. Meer gevorderde rekenaars schrijven € 7,- als er geen centen in het antwoord zitten.
Als je met je gezin in het buitenland woont zet je het geldteken van het land er voor. Behalve wanneer het een Nederlandse rekenmethode is, dan wijs je je kind erop dat hij/zij het euroteken mag gebruiken.
Vermenigvuldigen met kommagetallen. Bekijk de video:
Oefenbladen Rekenen Groep 7 (Gratis)
Oefenbladen Rekenen Groep 8 (Gratis)
Bekijk ook:
- Kommagetallen oefenen
- Kommagetallen delen
- Kommagetallen optellen
- Minsommen met kommagetallen
- Rekenen groep 7
- Rekenen groep 8
- Rekenregels: wat is de juiste volgorde van bewerkingen?





Gedifferentieerd huiswerk waarbij leerlingen kommagetallen vermenigvuldigen met 5, 10, 25, 50, 100 en 1000. Bovenaan op het werkblad vinden leerlingen een geheugensteuntje over hoe ze bepaalde oefeningen moeten oplossen.
Ja klopt. Heel erg handig nu ik het zo bekijk.
heel handig, bedankt.