
In groep 7 en 8 krijgt je kind te maken met het rekenonderdeel ‘delen met kommagetallen‘. Je wilt hulp bieden bij dit onderdeel van rekenen, maar hoe pak je dat aan? Je leest het in dit artikel!
Overzicht van de leerlijn ‘delen’
Eerst laten we zien hoe de basisschool toewerkt naar het (leren) maken van de sommen ‘delen met kommagetallen’. Hier volgt een globaal overzicht van de leerlijn ‘delen’ in de basisschool:

Wat je kind ook moet weten voordat het aan delen van kommagetallen begint:
- Wat links en rechts is. Tip: schrijf een R op de rechterhand en een L op de linkerhand;
- Voldoende kennis van de keer- en deeltafels. Tip: gebruik een tafelkaart;
- Van hele getallen, kommagetallen maken. Het getal 2 bijvoorbeeld kan je ook als 2,0 schrijven;
- De komma bij deelsommen met 10, 100 of 1000 één, twee of drie plaatsen naar links zetten. Ezelsbruggetje: keer = de komma gaat naar rechts, delen = de komma gaat naar links
- Verwoorden hoe de bewerkingen deel en keer met elkaar samenhangen en dit met materiaal en op de getallenlijn kunnen laten zien.
Tafelkaarten
Zodra je merkt dat je kind het antwoord op de deelsommen niet (gemakkelijk) weet, dan mag je een deeltafelkaart (en eventueel ook een keertafelkaart) geven, zodat hij/zij de deelstappen van de som kan opzoeken. Het gaat er nu immers niet om of je kind de tafels kent maar dat het de strategie van de deelsommen gaat beheersen. Print hier de tafelkaarten.
Nogmaals de tip:
Als je merkt dat de keer- en deeltafels nog niet goed genoeg geautomatiseerd zijn, oefen dan dagelijks één tafel en dat voor bijvoorbeeld een week lang. Na een week oefen je een volgende deeltafel.
Termen die je tegen kunt komen bij delen met kommagetallen
In onderstaand overzicht vind je alle termen die je in rekenopgaven ‘delen met kommagetallen’ tegen kunt komen:
Hoe kommagetallen delen?
Er zijn twee verschillende manieren om kommagetallen te delen. Je kunt dit doen met behulp van
1 . een staartdeling: een staartdeling maakt gebruik van 2 schuine streepjes bij het opschrijven:
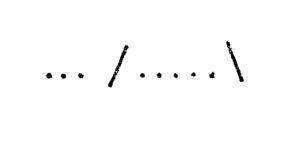
2 . de hapmethode: waar cijferend delen mee wordt bedoeld. De hapmethode maakt gebruik van een L op de kop en in spiegelbeeld:
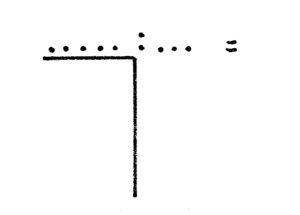
Bij beide manieren is de vaardigheid om te kunnen vermenigvuldigen en delen met getallen als 10, 100 of 1000 en kennis van de keertafels onmisbaar.
Kommagetallen delen door 10, 100 en 1000
Zoals ik al schreef is de vaardigheid om te kunnen vermenigvuldigen en delen met getallen als 10, 100 of 1000 onmisbaar. Dat komt omdat het getal waardoor je wilt delen (de deler) altijd een heel getal moet zijn. Om een (komma)getal met een kommagetal te moeten delen is nog veel te lastig voor kinderen van groep 7 en/of 8.
De techniek van vermenigvuldigen met 10, 100, of 1000 heeft je kind nodig wanneer de deler een kommagetal is en daar een heel getal van gemaakt moet worden. Dat gaat als volgt:
Kommagetal delen door 10
Voorbeeld:
12 : 0,2 =
Je maakt van 0,2 (de deler) een heel getal door het getal keer 10 te doen. MAAR….. dan moet het deeltal (12) OOK met 10 vermenigvuldigd worden. De nieuwe som is dan:
120 : 2 = 60
Dus zowel deler als deeltal moet met het zelfde getal vermenigvuldigd worden als je de komma wilt wegwerken (zie voor meer uitleg het kopje: “Hele getallen delen door kommagetallen” of “Cijferend delen met kommagetallen”).
Bij de sommen waarbij het kommagetal gedeeld mag worden door 10, gaat de komma 1 plaats naar links:
0,5 : 10 = 0,05
28,9 : 10 = 2,89
59,45 : 10 = 5,945
Kommagetal delen door 100
Bij de sommen waarbij het kommagetal gedeeld mag worden door 100, gaat de komma 2 plaatsen naar links:
34,9 : 100 = 0,349
15,91 : 100 = 0,1591
Mocht het getal, dat gedeeld mag worden, te weinig cijfers hebben om de komma te verplaatsen weet dan dat je er nullen voor mag schrijven om de komma het juiste aantal plaatsen te kunnen verschuiven.
0,12 : 100 = ?
Je kunt dan schrijven:
000,12 : 100 = 0,0012
Kommagetallen delen door 1000
Dit zelfde geldt voor : 1000 (en alle andere getallen met een één en verder alleen maar nullen).
Dus: keer 1000, dan gaat de komma drie plaatsen naar links.
Voorbeeld:
1528,2 : 1000 = 1,5282
0,68 : 1000 = 0,00068
Delen door bijvoorbeeld 100.000?
Dan gaat de komma 5 plaatsen naar links.
1,5 : 100.000 = 0,000015
Dit type sommen wordt in groep 7 aangeboden. De leerkracht van groep 8 gaat hiermee verder door uit te leggen hoe je kind kommagetallen kan delen door gebruik te maken van een staartdeling of met behulp van de hapmethode (cijferend delen).
Kommagetallen delen groep 8
In groep 8 leren kinderen kommagetallen op twee manieren te delen, namelijk met behulp van staartdelingen of via cijferend delen, ook wel de hapmethode genoemd. Als je een kind hebt dat baat heeft bij werken met één strategie, dan raad ik aan om de staartdeling te kiezen, deze goed uit te leggen en de strategie te laten automatiseren door regelmatig (kort) te oefenen.
Hier volgen 5 belangrijke regels:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 2: je voegt 0 of ,0 (lees: komma nul) aan het deeltal toe zodat je door kunt rekenen tot achter de komma en op 0 uitkomt
- regel 3: je schrijft een komma in het antwoord zodra je de komma in het deeltal passeert
De volgende twee regels gelden alleen bij staartdelingen:
- regel 4 a: als je al een begin hebt van het antwoord en je komt een getal tegen dat niet door de deler gedeeld kan worden, dan schrijf je een 0 in het antwoord, vervolgens mag je het volgende getal van het deeltal toevoegen aan het cijfer dat te klein was om te delen
- regel 4 b: als het cijfer voor de komma te klein is, schrijf je in je antwoord 0, en pas dan mag je het tweede cijfer in de staartdeling naar beneden halen
De volgende regel geldt alleen bij cijferend delen, ook wel de hapmethode genoemd:
- regel 5: eerst neem je een hap van het getal vóór de komma. Pas als je een kleine rest overhoudt voeg je alle cijfers daar aan toe en gaat verder met de hapmethode. Natuurlijk schrijf je wel eerst een komma in het antwoord!
In onderstaande video is een tip opgenomen over kommagetallen vermenigvuldigen en het delen met kommagetallen met een veelvoud van 10:
Cijferend delen met kommagetallen
Cijferend delen met kommagetallen wordt ook wel de hapmethode genoemd. Dat komt omdat je bij deze strategie kijkt wat de grootste hap is die je weg kunt nemen. Je kunt het zien als delen door herhaald aftrekken.
Voorbeeld 1 (hele getallen delen)
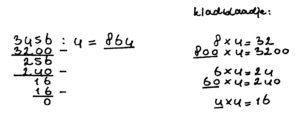
De onderstreepte cijfers in het rechter rijtje tel je bij elkaar op en je hebt het antwoord!
Voorbeeld 2 (kommagetallen delen door een kommagetal kleiner dan 1)
34,7 : 0,5 =
Bij deze som kun je het best de komma in de deler wegwerken door beide getallen te vermenigvuldigen met 10. We weten dat bij X 10 de komma 1 plaatsje naar rechts gaat en dat ook het deeltal met tien vermenigvuldigd wordt. De som wordt dus:
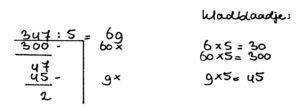
Let op: deze som bereken je verder door 0 toe te voegen. Dat ziet er als volgt uit:
De som wordt dan:
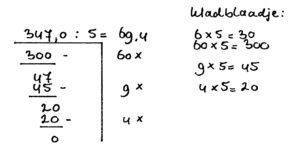
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 2: je voegt 0 of ,0 (lees: komma nul) aan het deeltal toe zodat je door kunt rekenen tot achter de komma en op 0 uitkomt
- regel 3: je schrijft een komma in het antwoord zodra je de komma in het deeltal passeert
Nog een voorbeeld:
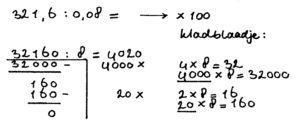
In bovenstaand voorbeeld is de volgende regel toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
Staartdelingen met kommagetallen
Veel kinderen vinden dit de makkelijkste manier om te delen. Voorstanders van de staartdeling zeggen dat deze manier minder gelegenheid geeft om fouten te maken. Staartdelingen zijn goed in te zetten wanneer het deeltal een kommagetal is.
Voorbeeld 1 (de drie voorbeelden zijn dezelfde sommen als bij het hoofdstuk ‘cijferend delen met kommagetallen’):
3456 : 4 = 864
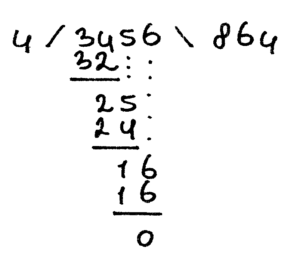
Voorbeeld 2 (kommagetallen delen door een kommagetal kleiner dan 1)
34,7 : 0,5 =
Ik ga beide getallen eerst vermenigvuldigen met 10 zodat ik geen kommagetal als deler heb. De som wordt dan:
347 : 5 =
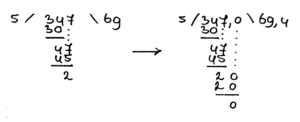
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 2: je voegt 0 of ,0 (lees: komma nul) aan het deeltal toe zodat je door kunt rekenen tot achter de komma en op 0 uitkomt
- regel 3: je schrijft een komma in het antwoord zodra je de komma in het deeltal passeert
Nog een voorbeeld:
321,6 : 0,08 =
eerst x 100, zodat de deler een heel getal wordt, dan krijg je:

Extra uitleg:
8 past 0 keer in 1, je schrijft een 0 in het antwoord en haalt het volgende cijfer naar beneden, in dit geval de 6.
8 past 2 keer in 16 en 16 – 16 = 0.
Er staat nog een 0 in het deeltal… ook die haal je naar beneden.
8 past 0 keer in 0 dus je schrijft nog een 0 in het antwoord en dan ben je klaar.
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 4 a: als je al een begin hebt van het antwoord en je komt een getal tegen dat niet door de deler gedeeld kan worden, dan schrijf je een 0 in het antwoord, vervolgens mag je het volgende getal van het deeltal toevoegen aan het cijfer dat te klein was om te delen.
Kommagetallen voorbeeldsommen
Nu volgen een aantal hoofdstukken waarin ik alleen voorbeeldsommen laat zien, gekoppeld aan één of meerdere regels/strategieën.
Kommagetallen delen door hele getallen
Voorbeeld 1 a (staartdeling):
44,585 : 5 =
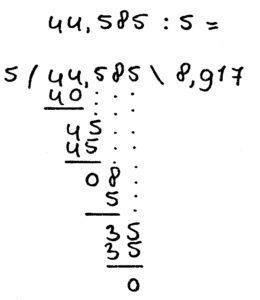
In bovenstaand voorbeeld is de volgende regel toegepast:
- regel 3: je schrijft een komma in het antwoord zodra je de komma in het deeltal passeert
Voorbeeld 1 b (cijferend delen):
44,585 : 5 = 8,917
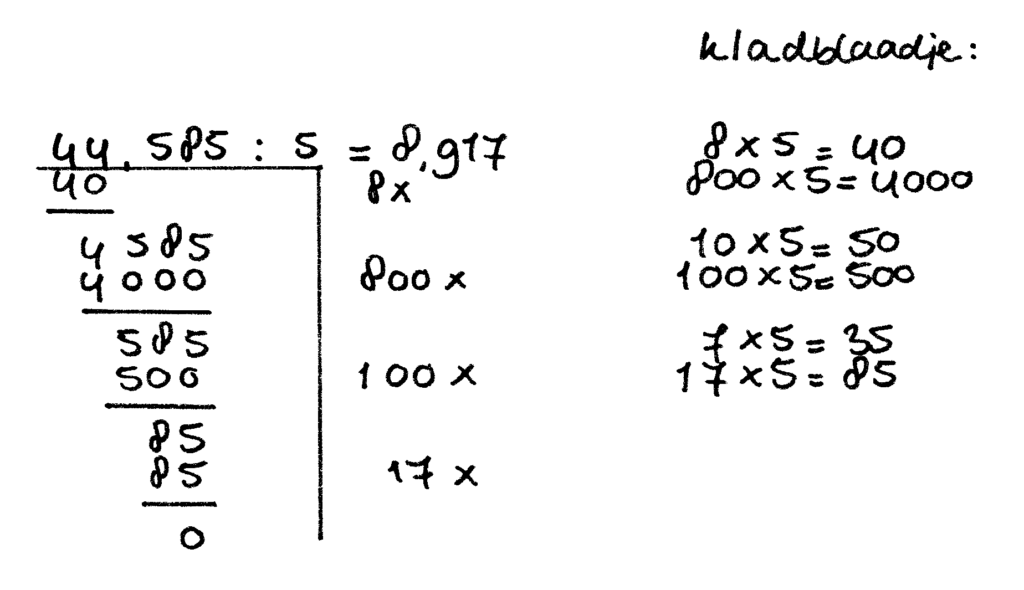
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 5: eerst neem je een hap van het getal vóór de komma. Pas als je een kleine rest overhoudt voeg je alle cijfers daar aan toe en gaat verder met de hapmethode. Natuurlijk schrijf je wel eerst een komma in het antwoord!
- regel 3: je schrijft een komma in het antwoord zodra je de komma in het deeltal passeert
Hele getallen delen door kommagetallen
16: : 0,2 = 80 want
160 : 2 = 80
In bovenstaand voorbeeld is de volgende regel toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
We weten al dat wanneer je de deler met tien vermenigvuldigd, je dit ook met het deeltal moet doen.
Voorbeeld van een staartdeling:
65 : 0,5 = 130 want:
650 : 5 =
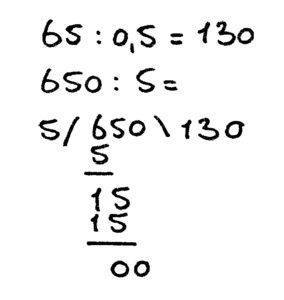
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 4 a: als je al een begin hebt van het antwoord en je komt een getal tegen dat niet door de deler gedeeld kan worden, dan schrijf je een 0 in het antwoord, vervolgens mag je het volgende getal van het deeltal toevoegen aan het cijfer dat te klein was om te delen
Voorbeeld van de hapmethode:
65 : 0,5 = 130 want:
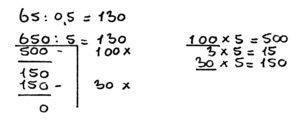
In bovenstaand voorbeeld is de volgende regel toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
Kommagetallen kleiner dan 1delen
Voorbeeld:
0,18 : 1,2 = (eerst keer 10) dan wordt het:
1,8 : 12 =
Voorbeeld van een staartdeling:
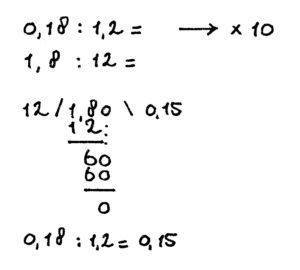
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 2: je voegt 0 of ,0 (lees: komma nul) aan het deeltal toe zodat je door kunt rekenen tot achter de komma en op 0 uitkomt
- regel 4 a: als je al een begin hebt van het antwoord en je komt een getal tegen dat niet door de deler gedeeld kan worden, dan schrijf je een 0 in het antwoord, vervolgens mag je het volgende getal van het deeltal toevoegen aan het cijfer dat te klein was om te delen
- regel 4 b: als het cijfer voor de komma te klein is, schrijf je in je antwoord 0, en pas dan mag je het tweede cijfer in de staartdeling naar beneden halen
Nog een voorbeeld maar nu berekend met behulp van de hapmethode. Het is voor een kind vaak lastiger om alle handelingen uit elkaar te houden want bij het checken hoe vaak 8 in een getal gaat moet je onderscheid maken tussen voor en na de komma!!
4,40 : 0,8 =
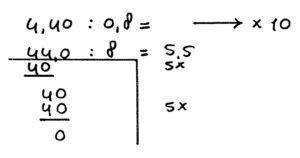
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 5: eerst neem je een hap van het getal vóór de komma. Pas als je een kleine rest overhoudt voeg je alle cijfers daar aan toe en gaat verder met de hapmethode. Natuurlijk schrijf je wel eerst een komma in het antwoord!
Het zelfde voorbeeld maar nu berekend met behulp van een staartdeling.
4,40 : 0,8 =
44 : 8
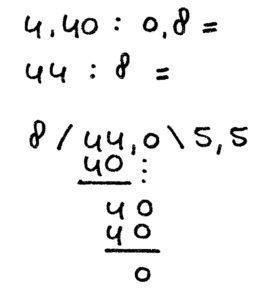
In bovenstaand voorbeeld zijn de volgende regels toegepast:
- regel 1: zorg dat je geen kommagetal hebt als deler (dat is het getal waardoor je gaat delen en is het tweede getal in een som)
- regel 2: je voegt 0 of ,0 (lees: komma nul) aan het deeltal toe zodat je door kunt rekenen tot achter de komma en op 0 uitkomt
- regel 3: je schrijft een komma in het antwoord zodra je de komma in het deeltal passeert
Kommagetallen delen door kommagetallen
Kijk zelf welke regels je hier moet toepassen.
Een voorbeeld:
11,25 : 0,9

Jaarlijks geeft een reken Cito vraag aan dat het antwoord in twee decimalen opgeschreven moet worden.
In bovenstaande som mag (moet!) je dan een 0 achter de 5 schrijven.
Een voorbeeld van een moeilijke som:
6,06 : 1,2 =
Eerst x 10, zodat ik geen komma getal als deler heb. Dat wordt dan:
60,6 : 12 =
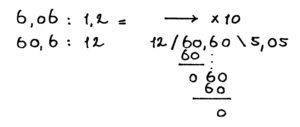
Omdat 6 te klein is om door 12 te delen voeg ik een nul toe aan het antwoord. Vervolgens voeg ik een nul toe aan het deeltal. Nu kan ik een nul naar beneden halen en dan kan ik verder gaan met delen.
Het laatste voorbeeld:
6,5 : 0,25
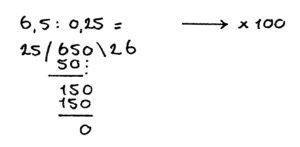
Na het lezen van deze uitleg heb je niet alleen ervaren dat je ‘delen met kommagetallen’ op verschillende manieren kunt berekenen maar ook dat er veel verschillende ‘regels’ zijn om toe te passen.
Geduld en veel oefenen zijn dan ook de sleutelwoorden om je kind te helpen bij het uitrekenen van deze sommen. Uiteindelijk zal het een automatisme worden en kan je kind met vertrouwen de Cito toets tegemoet zien. 😉
SUCCES!

Oefenbladen Rekenen Groep 8 (Gratis)

Oefenbladen Rekenen Groep 7 (Gratis)
Voor oefenen met kommagetallen op het juiste niveau, kun je één van de oefenboeken rekenen bestellen:
-
Breuken en Procenten oefenpakket + videobijles (Cito – IEP)
Oorspronkelijke prijs was: 119,75.87,00Huidige prijs is: 87,00. BundelkortingIn mijn winkelwagen Bekijk detailsVideobijles Rekenen Groep 7
Oorspronkelijke prijs was: 79,00.49,95Huidige prijs is: 49,95. Aanbieding!In mijn winkelwagen Bekijk detailsOefenboeken Doorstroomtoets Groep 8 deel 1 + deel 2
Oorspronkelijke prijs was: 54,00.39,95Huidige prijs is: 39,95. BUNDELKORTINGIn mijn winkelwagen Bekijk detailsOefenboeken Rekenen Groep 8 – deel 1 + 2
Oorspronkelijke prijs was: 54,00.39,95Huidige prijs is: 39,95. BundelkortingIn mijn winkelwagen Bekijk detailsGerelateerde artikelen
Reacties
4 reacties op “Kommagetallen delen: de enige uitleg met veel voorbeelden”Geef een reactie



















super bedankt
Graag gedaan Hailey!
Succes!
Hartelijke groet,
Carola
Kunt u een video maken over delen met komma getallen met een hapmethode? Groep 7
Hoi Israa,
Daar hebben we helaas nog geen video over, maar ik zal je proberen uit te leggen hoe dat werkt.
Als je bijvoorbeeld de som 321,6 : 0,08 hebt, haal je eerst de komma uit de deler door de deler x 100 te doen. Maar als je het ene getal x 100 doet, moet je het andere getal ook x 100 doen want anders is het niet eerlijk.
Dan krijg je:
32160 : 8
En dan kun je de hapmethode doen.
32160 : 8 =
32000 – | 4000 x
160 |
160 – | 20 x
0
32160 : 8 = 4020
dus 321,6 : 0,08 = 4020
Ik hoop dat je het nu snapt.
Succes!
Groetjes,
Carola