Hoe je je kind kunt helpen bij het gelijknamig maken van breuken


Breuken gelijknamig maken….inzicht komt voor het trucje. Naarmate sommen met breuken moeilijker worden, vallen kinderen meer terug op het gebruiken van trucjes. Zo ook bij het gelijknamig maken van breuken.
Maar al te vaak gaat dit mis: ze verwarren 2 trucjes met elkaar, of weten alleen nog maar de eerste stap. Om dit te voorkomen is het nodig dat er eerst inzicht is. Kinderen zouden de trucjes eigenlijk eerst zelf uit moeten uitvinden, zodat ze altijd op begrip kunnen terugvallen.
Het Freudenthalinstituut zegt er het volgende over:
“Kennis van rekenregels is kwetsbaar als het niet op begrip is gebaseerd. Omgekeerd kan een leerling die het in een bepaalde situatie gewenste rekenregeltje niet kent, toch een heel eind komen met inzicht in breuken en verhoudingen”
In dit artikel laat ik je zien hoe je je kind daarbij kan helpen.
Gelijknamig maken van breuken – wat eraan voorafgaat
Vanaf groep 4 worden de breuken geïntroduceerd op de basisschool. Meestal met heel concrete voorbeelden: een halve appel, een kwart boterham of een kwart uur.
In groep 5/6 worden daar nog meer breuken aan toegevoegd: vijfden, achtsten, tienden, derden en zesden. Je kind leert waar deze breuken staan op de getallenlijn. Ook wordt de relatie gelegd tussen bijvoorbeeld 1/4 en de omschrijving ‘een kwart van de Nederlanders’ of, als verhouding, 1 op de 4 Nederlanders.
Er worden ook kale sommen gemaakt met breuken zoals: 3/4 – 2/4 =.
En je kind moet ook kunnen uitrekenen hoeveel ieder krijgt als je 2 pizza’s verdeelt met z’n drieën. Meestal wordt de oplossing gevonden door de pizza’s te tekenen. Verdeel iedere pizza in 3 stukken. Ieder kind krijgt 2 van die stukken, dus het antwoord is dan een breuk: 2/3.
Verder leert je kind welke breuken gelijkwaardig zijn. En daar gaat het vaak mis. Want op het moment dat dit niet meer met tekeningen of materiaal ondersteund wordt, blijft alleen het ‘trucje’ over: een gelijkwaardige breuk vind je door teller en noemer met hetzelfde getal te vermenigvuldigen. Maar bij een andere breukensom moet je de teller en de noemer juist door hetzelfde getal delen (vereenvoudigen), of de noemer van de teller aftrekken (helen eruit halen), of de noemer van de ene breuk met die van de andere vermenigvuldigen (gelijknamig maken).
Het is dus niet zo raar dat je kind al die trucjes door elkaar gaat halen. Het goede nieuws is dat je kind lang niet al die trucjes hoeft te onthouden. Als het eenmaal goed begrijpt hoe het zit, heeft het er meestal genoeg aan om even een tekeningetje (taart) te maken op een kladblaadje om de som op te lossen.
Een uitzondering hierop vormt het gelijknamig maken van de breuken. Dat lukt niet door te tekenen, dus een trucje is hier wel op zijn plaats. Maar ook hier geldt: begrip komt vóór het trucje.
Download hier de (gratis) Werkbladen Breuken Groep 6/7/8
Oefenbladen Rekenen Groep 6 (Gratis)
Even in de herhaling: gelijkwaardige breuken
Dit artikel gaat over het gelijknamig maken van breuken, maar dat kan je kind pas goed snappen als het echt snapt wat gelijkwaardige breuken zijn. Daarom gaan we daar eerst nog even mee aan de slag.
Hieronder vind je gekleurde breukenrepen, waarin delen die even groot zijn dezelfde kleur hebben.
Download de gekleurde breukenrepen
Ze zijn alleen op een andere manier verdeeld. Maar je ziet gelijk dat de roze vlakken allemaal even groot zijn: 1/2 = 2/4 = 3/6 = 4/8 = 5/10. Ze zijn allemaal gelijkwaardig. Dat geldt ook voor de andere vlakken die dezelfde kleur hebben. De bedoeling is dat je kind echt gaat snappen dat als je de stukjes kleiner maakt, dat er dan meer stukjes in een hele passen. Hoe groter de noemer, hoe kleiner de stukjes en andersom. Dus:
Teller = hoeveel stukjes heb je?
Noemer = in hoeveel stukjes is de hele verdeeld?
Laat je kind dit ook allemaal zelf ontdekken met behulp van breukencirkels. Hier vind je een link waarmee je breukencirkels kunt downloaden:
Download de breukencirkels
Print het bestand en knip de breukencirkels uit. Houd van iedere breukencirkel één cirkel heel en knip de andere in stukken. Nu kan je kind zelf gaan passen en meten wat bijvoorbeeld allemaal precies in een halve cirkel past, en wat er even groot is als 1/3. Deze delen zijn allemaal even groot, dus gelijkwaardig. Je zegt dan ook dat 1/3 en 2/6 gelijkwaardig zijn. En dat is iets anders dan gelijknamig. Gelijknamige breuken hebben namelijk – het woord zegt het al – gelijke namen, dus gelijke noemers.
1/6 en 3/6 zijn dus gelijknamig, maar niet gelijkwaardig.
Gelijknamig maken van breuken groep 7
Tot nu toe werden breuken steeds heel concreet aangeboden. In een context van pizza’s, repen en taarten. Ook bij de kale sommen in groep 5/6 was het niet lastig om er concrete voorstellingen bij te maken.
Vanaf rekenen in groep 7 wordt het allemaal een beetje abstracter, en daardoor beginnen kinderen breuken vanaf dat moment als moeilijk te ervaren. Ze proberen enig houvast te krijgen door trucjes te gebruiken, maar halen uiteindelijk alle trucjes door elkaar.
Tijd om de breukencirkels weer in te zetten. Dit artikel gaat over het gelijknamig maken van breuken, dus daar gaan we mee aan de slag.
We maken er even een verhaaltje van:
Op een feestje met 12 mensen eet je pizza. Je hebt 3 verschillende even grote pizza’s. Aan het eind van de avond is van de ene pizza nog 1/3 deel over, van de andere nog 1/6 deel.
De vraag is: Hoeveel pizza is er nog in het totaal over?
Pak nu de breukencirkels, en pak de delen die je nodig hebt. Dus 1/3 deel en 1/6 deel. Leg ze in een cirkel. Kun je nu in één breuk zeggen hoeveel er nog over is? Nee, want de noemers zijn niet gelijk. Breuken met verschillende noemers kun je niet bij elkaar optellen, net zoals je appels en peren niet bij elkaar op kunt tellen. Dat kan wel als je ze dezelfde naam (noemer) geeft: 5 appels en 3 peren zijn 8 vruchten.
Bij de breuken moeten we dus ook de noemers (namen) gelijk maken. Wat betekent dat? Dat we de stukken even groot moeten gaan maken, want stukken die even groot zijn hebben dezelfde noemer.
Van 1/6 kunnen we geen 1/3 maken. We kunnen het stuk pizza niet groter maken dan het is. Maar het stuk van 1/3 kunnen we wel doormidden snijden.
Hoeveel punten zou je dan krijgen als de pizza nog heel zou zijn? Dan zou je zes punten krijgen. Maar je hebt nog maar 1/3 deel over, dus dan heb je ook maar 6 : 3 = 2 punten van 1/6 pizza, dus 2/6 pizza. Maar dat wisten we al: 1/3 is gelijk aan 2/6.

Laat dit allemaal zien met de breukencirkels!
Nu kun je de stukken van 1/6 bij elkaar leggen. Ze zijn nu gelijknamig gemaakt.
Bij elkaar heb je nu 1/6 + 2/6 = 3/6 pizza.
Bij breukensommen moet je altijd kijken of het antwoord nog ‘vereenvoudigd’ kan worden, dat betekent niets anders dan dat
je kleine stukjes aan elkaar plakt tot grotere, zonder dat er stukjes over blijven. Als de stukjes groter worden, wordt de noemer kleiner.
Je kunt dus ook zeggen dat:
Vereenvoudigen = een gelijkwaardige breuk zoeken waarvan de noemer zo klein mogelijk is.
Het trucje is: zoek een zo hoog mogelijk getal waardoor je de teller en de noemer alle twee kunt delen.
In dit voorbeeld vereenvoudig je de breuk 3/6 door er 1/2 van te maken. Je deelt teller en noemer dus door 3.
Het geheim van breuken gelijknamig maken
Maar stel nou dat je ook nog een stuk van 1/5 over hebt. Dan heb je dus een halve pizza en 1/5. Je kunt geen halve pizza maken met alleen maar stukken van 1/5, dus hoe kun je de noemers nu gelijk maken (dus de stukken even groot maken)? Laat je kind zelf eerst even puzzelen met behulp van het strokenschema (de gekleurde breukenrepen) of met de breukencirkels. Bedenkt het zelf dat 1/5 even groot is als 2/10? En dat je die halve ook in tienden kunt verdelen? Dan heeft het een belangrijke stap gezet: 1/5 + 1/2 is hetzelfde als 2/10 + 5/10. En dat is dus 7/10.
Je kind zal nu niet meer zo gauw de vergissing maken dat het antwoord 7/20 is. De noemer is alleen een naam, en die verandert niet als je er meer van hebt (2 kikkers + 5 kikkers = 7 kikkers en niet opeens 7 goudvissen).
Waarom was deze tweede som (1/2 + 1/5) moeilijker dan de eerste (1/3 + 1/6)? Omdat bij de tweede som alle twee de breuken een nieuwe noemer moesten krijgen. In het schema kun je zien dat zowel 1/2 als 1/5 in tienden verdeeld kunnen worden. Dat komt omdat zowel in de tafel van 2 als in de tafel van 5 het getal 10 voorkomt. Dit getal noem je dan de ‘gemene deler’. In de tafel van 5 en 10 zit natuurlijk ook 20, maar het gaat erom de kleinste gemene deler te vinden.
Kennis van de tafels, maar vooral ook van de getallen die in meerdere tafels voorkomen, is dan belangrijk. Onderaan dit artikel staat een link naar een spelletje dat je zelf kunt printen en waarmee je kind juist dit laatste kan oefenen.
Het geheim van het gelijknamig maken zit hem dus in het vinden van een getal dat in de tafels van alle twee de noemers zit van de breuken die je moet optellen (de zogenaamde gemene deler). Als je bijvoorbeeld 1/3 en 1/8 moet optellen, is dat het getal 24. Want 3 x 8 = 24 en 8 x 3 ook. Je ziet nu gelijk dat dat getal heel makkelijk te vinden is door de noemers met elkaar te vermenigvuldigen.
Maar als je van 1/3 een breuk wil maken met als noemer 24, dan moet je weer de ‘truc’ van het gelijkwaardig maken gebruiken: teller en noemer met hetzelfde getal vermenigvuldigen.
1 x 8 = 8
3 x 8 = 24
Hetzelfde doe je met 1/8
1 x 3 = 3
8 x 3 = 24
Nu kun je ze optellen (of aftrekken): 8/24 + 3/24 = 11/24. Deze breuk kun je niet vereenvoudigen, omdat 11 en 24 niet door eenzelfde getal gedeeld kunnen worden.
Breuken gelijknamig maken: het trucje
Best een ingewikkeld verhaal allemaal, het is ook niet voor niets dat veel kinderen de weg kwijtraken en de trucjes voor het gelijknamig maken, gelijkwaardig maken en vereenvoudigen door elkaar halen. Voor de laatste twee hoeven ze ook eigenlijk geen trucjes te onthouden. Als ze veel geoefend hebben met de breukencirkels kunnen ze dit soort sommen ook altijd oplossen door deze cirkels te tekenen. Ze tekenen bijvoorbeeld 1/3 en zien dan dat je daar 6 stukken van kunt maken door alle stukken doormidden te delen. En dat in 1/3 dus 2 stukken van 1/6 passen.
Voor het gelijknamig maken is het wel veel eenvoudiger als ze het trucje zouden kunnen onthouden. En dat wordt makkelijker door gebruik te maken van een tekeningetje: de vlinder:
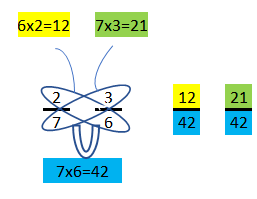
Hoe werkt het? Schrijf de 2 breuken die je gelijknamig moet maken naast elkaar op. Teken de vleugels, dus zet een cirkel om de noemer van de ene breuk en de teller van de andere breuk. De getallen in de vleugels vermenigvuldig je met elkaar, dus 6 x 2 = 12. Dat antwoord zet je bij de voelspriet. Zo ook met 7 x 3.
Om de gezamenlijk noemer te vinden vermenigvuldig je vervolgens de noemers met elkaar (dan weet je zeker dat je een getal hebt dat in alle twee de tafels zit). Nu hoef je alleen nog maar de 2 breuken op te schrijven en dan kan je ze optellen door de tellers bij elkaar te tellen. Het antwoord hier is dus 33/42.
Nu nog vereenvoudigen: beide getallen zijn deelbaar door 3, dus 11/14. Ziet je kind niet in 1 keer dat beide getallen door 3 te delen zijn? Dan is het een kwestie van uitproberen: eerst door 2, dan door 3 en eventueel nog door 5 of 7.
In dit voorbeeld staan de sommen helemaal uitgeschreven bij de vlinder. Dat hoeft natuurlijk niet, het is voldoende als de antwoorden er staan. Dus, even een ander voorbeeld:
Nu kun je de breuken optellen, met als uitkomst 21/35 of aftrekken, dat wordt 11/35.
Deze uitkomsten kunnen niet verder vereenvoudigd worden.
Ten slotte, heel belangrijk: alleen als je ongelijknamige breuken moet optellen of aftrekken, moet je ze eerst gelijknamig maken! Dus voor vermenigvuldigen of delen geldt dat niet!

Download “Tafelen” (gratis spelletje!)
- Breuken oefenen: de complete handleiding
- Breuken optellen
- Breuken aftrekken
- Breuken vermenigvuldigen
- Breuken gelijknamig maken
- Breuken vereenvoudigen
- Kleinste gemene veelvoud
- Procenten berekenen
- Breuken groep 6
- Deel van het geheel berekenen
- Breuken op de getallenlijn plaatsen
- Zo gebruik je een breukenposter





