Breuken optellen: uitleg, voorbeelden en oefenen (+ PDF)

Breuken optellen uitleg
Ongelijknamige breuken optellen
Breuken optellen: video
Breuken optellen met helen
Minsommen met breuken
Minsommen met ongelijknamige breuken
Minsommen met breuken: video
Breuken aftrekken van helen
Hoe kun je je kind helpen met breuken?

Het optellen en aftrekken met breuken komt in de hogere groepen van de basisschool aan de orde. Toch leren kinderen in de kleuterklassen al hoe ze dingen moeten verdelen. Vanaf groep 6 worden breuken als getallen aangeboden tijdens de rekenles. Daarna vormt de kennis van breuken een basis voor het berekenen van procenten.

In eerdere artikelen wordt het gelijknamig maken van breuken uitgelegd. Bekijk die uitleg eerst voordat je met het optellen van breuken aan de slag gaat.

Breuken optellen uitleg

Breuken zijn voor veel kinderen lastig bij het oefenen van rekenen. Het is daarom belangrijk om breuken zo concreet mogelijk te maken, zodat kinderen zien wat een breuk nu eigenlijk is. Dit kan bijvoorbeeld met stroken, pizza’s, pannenkoeken, repen chocolade, snoepjes, koekjes, taarten, enzovoort. Vooral het handelend bezig zijn met deze materialen zorgt voor begripsvorming.

Bijvoorbeeld: je bestelt samen met je kind een pizza en laat je kind de pizza in acht stukken verdelen. Als je hier een breuk van maakt, schrijf je dit zo: 8/8. Elk stuk van de pizza is 1/8 deel van de hele pizza.

Het bovenste getal van een breuk noemen we de teller, omdat dit getal aangeeft hoeveel delen er zijn. Het onderste getal van een breuk noemen we de noemer. De noemer geeft aan hoe een deel heet, hoe groot een stuk is. Bijvoorbeeld: 1/8 betekent dat iets verdeeld is in acht stukken en dat je één van deze acht stukken hebt. Als de teller en de noemer even groot zijn, heb je hele. Bijvoorbeeld: 4/4 → een taartje is verdeeld in vier stukken en je hebt alle vier de stukken, dus het hele taartje. Of: 6/6 → een pizza is verdeeld in zes stukken en je hebt alle zes de stukken, dus de hele pizza.

Nadat jullie de pizza in acht stukken hebben verdeeld, eten jullie allebei één stuk pizza op. Dit betekent dat jullie samen 2/8 deel van de pizza hebben opgegeten: je kind heeft 1/8 deel van de pizza opgegeten en jij hebt ook 1/8 deel van de pizza opgegeten → 1/8 + 1/8 = 2/8. De breuken die je in deze som bij elkaar optelt zijn gelijknamig: ze hebben dezelfde ‘naam’, dezelfde noemer. Het zijn allebei ‘achtsten’.

Download hier de (gratis) Werkbladen Breuken Groep 6/7/8

Oefenbladen Rekenen Groep 6 (Gratis)

Ongelijknamige breuken optellen

Bij het optellen van ongelijknamige breuken moet je de noemers eerst gelijk maken. Je probeert de noemers zo klein mogelijk te maken.

Stel dat je twee pizza’s hebt besteld voor jou en je kind. Jij snijdt je pizza in vier stukken en je kind snijdt zijn pizza in acht stukken. Jij eet één stuk van jouw pizza op en je kind eet twee stukken van zijn pizza op. Je wilt weten hoeveel pizza jullie samen al opgegeten hebben.

Als je hier een som van maakt, ziet dat er als volgt uit:

1/4 + 2/8 =

Omdat de noemers niet hetzelfde zijn moeten we deze eerst gelijknamig maken. Hierbij proberen we de breuk zo klein mogelijk te maken. Je kunt van beide noemers vier maken. De vier van ¼ blijft een vier. Van de acht van 2/8 maak je een vier door deze te delen door twee. Maar als je de noemer deelt door twee, moet je ook de teller delen door twee:

Je kunt ook aan je kind laten zien dat dit klopt door het te tekenen:

De som wordt dan 1/4 + 1/4 = 2/4.

De uitkomst kun je vervolgens ook nog kleiner maken door de noemer te verkleinen.

4 : 2 = 2 en als je de noemer deelt door twee, moeten je ook de teller delen door twee → 2 : 2 = 1, dus kun je 2/4 verkleinen naar 1/2 → 1/4 + 1/4 = 2/4 = 1/2

Soms zijn er ook sommen waarbij het lastiger is om de breuken gelijknamig te maken. Je kunt de noemers dan niet gelijk maken door ze door hetzelfde getal te delen. Dan kun je de noemers het beste met elkaar vermenigvuldigen. Hierdoor worden ze groter, maar kun je ze wel gelijk maken.

Bijvoorbeeld: je hebt nog 3/7 deel van een pizza over en je vriend heeft nog 2/6 deel van een pizza over. Je wilt graag weten hoeveel pizza jullie nog over hebben.

De som wordt dus: 3/7 + 2/6 =

Je begint met het gelijknamig maken van de breuk door de noemers met elkaar te vermenigvuldigen: 7 x 6 = 42

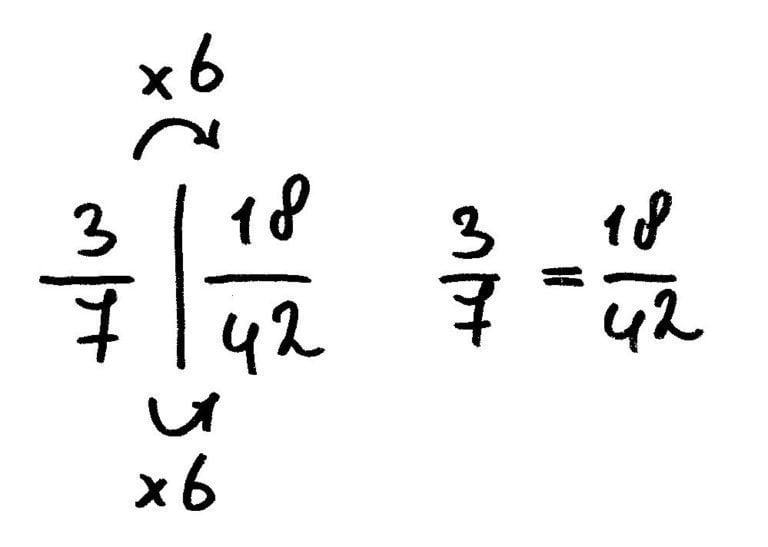
De breuken zijn gelijknamig gemaakt en hebben nu dezelfde noemer. Nu kun je de breuken bij elkaar optellen: 18/42 + 14/42 = 32/42

32/42 kun je nog vereenvoudigen à 32 en 42 kun je allebei delen door 2 → 32/42 = 16/21

In onderstaande video zie je nogmaals een uitleg over het optellen van breuken. Hierbij komt ook het optellen van breuken met ongelijknamige breuken aan bod.

De uitleg over breuken optellen is in dit artikel ook als tekst opgenomen.

Breuken optellen: video

https://www.youtube.com/watch?v=M79qUuwz9eU

We hebben vereenvoudigde breuken en deze gaan we optellen.

Voorbeeld:

3/5 + 7/9

Zoals eerder behandeld moeten we daartoe de breuken gelijknamig maken, dat wil zeggen: van een gelijke noemer voorzien.

Op zoek naar het kleinste gemene veelvoud (deelbaar door beide noemers) ligt het voor de hand de bestaande noemers met elkaar te vermenigvuldigen, waarmee de nieuwe noemer voor beide breuken 45 wordt.

Een kleiner getal dat deelbaar is door zowel de ene noemer als de andere en dat gehele getallen oplevert, bestaat in dit geval niet.

Teller en noemer vervolgens -per breuk- met het zelfde getal te vermenigvuldigen. Voor de eerste breuk moeten we de noemer (5) met 9 vermenigvuldigen om 45 te krijgen en de teller dus ook.

We krijgen 27/45.

De tweede breuk: teller en noemer vermenigvuldigen met 5 (immers 5 x 9 levert ook 45 op). Deze wordt dan 35/45.

Bij gelijknamige noemers kun je breuken optellen door de tellers op te tellen en door de gelijknamige, gemeenschappelijke noemer te delen. Nu de noemers in het voorbeeld gelijk zijn gemaakt, kunnen we de tellers dus bij elkaar optellen en het resultaat van de optelsom luidt dan:

27/45 + 35/45 = 62/45

Wanneer we breuken optellen zien we vaak dat er in de teller een getal komt te staan dat groter is dan de (nieuwe) noemer. Zo ook in dit geval: 62 torent uit boven de 45. We kunnen nu het antwoord vereenvoudigen: uit de teller (62) kunnen we één keer 45 weghalen en voor in het antwoord plaatsten.
We houden dan in het breukgedeelte van het antwoord 62-45=17 voor de teller over.

Het uiteindelijke antwoord luidt daarmee 1 17/45 (één zeventien vijfenveertigste)

Breuken komen voor in getallen die ook eenheden, tientallen, duizendtallen enzovoorts omvatten. We vonden er zojuist één in het antwoord van de optelling: 1 17/45.

Breuken optellen met helen

Als je denkt aan een pizza of een taart, kun je ook tellen met helen. Stel dat je bij de bakker komt om taarten te kopen voor je verjaardag. In de vitrine heeft de bakker allerlei taarten staan. Je ziet rijstevlaai staan. Hier wil je een hele vlaai en een halve vlaai van. Dus 1 1/2 rijstevlaai. Daarnaast zie je abrikozenvlaai. Hier wil je een hele vlaai en een kwart vlaai van, dus 1 ¼ abrikozenvlaai. Als je wilt weten hoeveel vlaai je nu hebt, moet je deze twee breuken bij elkaar optellen.
De som wordt dus:

1 1/2 + 1 1/4 =

Je telt eerst de helen bij elkaar op: 1 + 1 = 2.

Vervolgens tel je de breuken bij elkaar op: ½ + ¼. Deze moet je eerst gelijknamig maken → ½ = 2/4.

Nu kun je de breuken bij elkaar optellen: 2/4 + ¼ = ¾.

Vervolgens tel je de helen en de breuk bij elkaar op:

1 ½ + 1 ¼ = 1 2/4 + 1 ¼ = 2 ¾

Nog een voorbeeld:

4 5/7 + 8 3/9 =
Je telt eerst de helen bij elkaar: 4 + 8 = 12
Vervolgens maak je de breuken gelijk. Om de noemers gelijk te maken, moet je ze in dit geval met elkaar vermenigvuldigen: 7 x 9 = 63

De breuken hebben nu dezelfde noemer. Je kunt de breuken bij elkaar optellen:

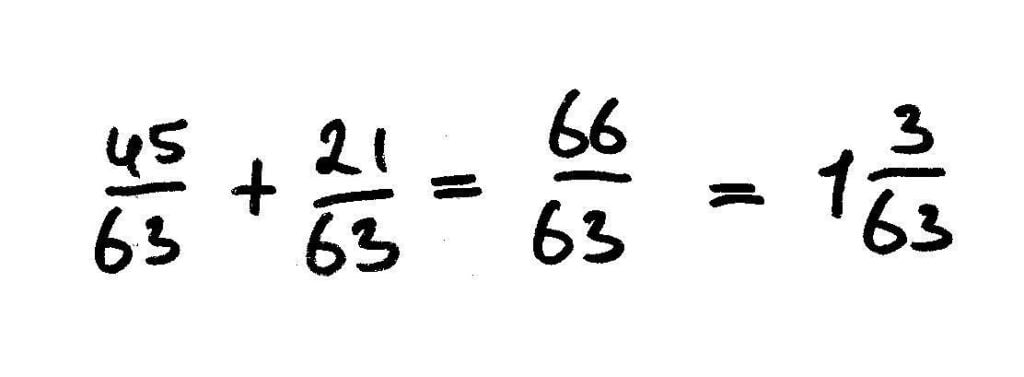
De teller is groter dan de noemer: 66/63. Eén hele is 63/63. Je hebt dan nog 3/63 over → 1 3/63.

De hele som ziet er als volgt uit:

Minsommen met breuken

Bij het aftrekken van breuken geldt hetzelfde als bij het optellen: als de noemers hetzelfde zijn, kun je de breuken bij elkaar optellen en als de noemers ongelijk zijn moeten deze eerst gelijk gemaakt worden.

Stel je hebt een reep chocolade waarvan nog 8/12 over is. Dus acht blokjes van de twaalf die er waren.

Je eet drie stukjes van de chocoladereep op, dus 3/12. Je wilt weten hoeveel stukjes je dan nog over hebt. De som wordt:

8/12 – 3/12 = 5/12

In deze som zijn de noemers gelijk en hoef je alleen de tellers van elkaar af te trekken.

Minsommen met ongelijknamige breuken

Ook bij de minsommen kun je breuken tegenkomen die ongelijknamig zijn. Hierbij moet je de noemers eerst weer gelijk maken. Je maakt de noemers weer zo klein mogelijk.

Een pizzaverkoper heeft nog 6/8 pizza liggen. Er komt een klant en die vraagt om een punt van ¼ pizza. De pizzaverkoper wil weten hoeveel pizza er dan over blijft.

De som wordt: 6/8 – 1/4 =

Je kunt van beide noemers 4 maken. De 4 in ¼ blijft 4 en de 8 in 6/8 delen we door 2 zodat deze ook 4 wordt → 8 : 2 = 4

Hetzelfde doe je dan met de tellers van de breuk: de 1 in ¼ blijft 1 en de 6 in 6/8 delen we net als de noemer door 2 → 6 : 2 = 3

Dus de som wordt: 3/4 – 1/4 = 2/4

De uitkomst kun je vervolgens ook nog kleiner maken door de noemer en de teller weer te verkleinen: 4 : 2 = 2 en 2 : 2 = 1, dus kun je 2/4 verkleinen naar ½ → ¾ – ¼ = 2/4 = ½

Let op: als je de noemer deelt of vermenigvuldigt, moet je hetzelfde doen met de teller! Anders klopt het niet meer. Bijvoorbeeld: als je bij 2/4 alleen de noemer deelt door twee, krijg je 2/2. 2/2 is hetzelfde als een hele en dus een heel andere breuk dan 2/4. Maar als je de noemer én de teller deelt door twee klopt het weer: 2/4 = ½. Teken het maar eens.

Bij de minsommen zijn er net als bij de plussommen sommen die lastiger zijn om gelijknamig te maken. Hierbij kun je de noemers niet verkleinen, maar moet je ze juist groter maken. Je vermenigvuldigt de noemers dan met elkaar.

Ook nu heeft de pizzaverkoper weer pizza liggen. Dit keer heeft hij 3/4 pizza liggen. Er komt een klant binnen en die vraagt om drie stukken van een 1/5 pizza. De pizzaverkoper wil graag weten hoeveel hij over houdt.

De som wordt: 3/4 – 3/5 =

Je begint met het vermenigvuldigen van de noemers, zodat deze gelijk worden: 5 x 4 = 20

De noemers zijn gelijk gemaakt. Dan wordt de som 15/20 – 12/20 = 3/20

Minsommen met breuken: video

https://www.youtube.com/watch?v=ASnH1ZjZajg

Breuken aftrekken van helen

Bij het aftrekken met helen zijn er drie verschillende manieren om dit te doen.

1. Minsommen waarbij de noemers gelijk zijn

De pizzaverkoper heeft nog 6 5/6 pizza. ’s Middags komt er een klant die drie hele pizza’s en drie stukken van 1/6 pizza wil kopen. De pizzaverkoper wil weten hoeveel pizza hij nog over heeft.

De som wordt: 6 5/6 – 3 3/6 =

Je haalt eerst de helen van elkaar af: 6 – 3 = 3

Dan haal je de breuken van elkaar af: 5/6 – 3/6 = 2/6

6 5/6 – 3 3/6 = 3 1/3

2. Minsommen waarbij de noemers ongelijk zijn

De pizzaverkoper heeft nog 7 4/5 pizza liggen. Een klant komt binnen en wil twee hele pizza’s en en 1/6 pizza kopen. De pizzaverkoper wil weten hoeveel hij over heeft.

De som wordt: 7 4/5 – 2 1/6 =

Eerst haal je de helen van elkaar af: 7 – 2 = 5

Dan moet je de noemers gelijk maken om de breuken van elkaar af te halen. Je vermenigvuldigt de noemers met elkaar: 5 x 6 = 30

4/5 = 24/30 (→ je vermenigvuldigt de teller en de noemer met 6)

1/6 = 5/30 (→ je vermenigvuldigt de teller en de noemer met 5)

De noemers zijn nu gelijk. Nu kun je de tellers van elkaar afhalen:

24/30 – 5/30 = 19/30

7 4/5 – 2 1/6 = →

7 – 2 = 5

24/30 – 5/30 = 19/30

7 4/5 – 2 1/6 = 5 19/30

3. Minsommen waarbij je een hele eerst moet verdelen in een breuk

De pizzaverkoper heeft nog 4 pizza’s liggen. Hij heeft honger gekregen en eet een stuk van 1/3 pizza op. Hoeveel pizza is er nog over?

De som wordt: 4 – 1/3 =

Van één van de hele maak je 3/3: 3 3/3 – 1/3 =

Nu kun je de breuken van elkaar afhalen.

4 – 1/3 → 3 3/3 – 1/3 = 3 2/3

Hoe kun je je kind helpen met breuken?

Het is belangrijk dat kinderen veel oefenen met breuken zodat ze echt gaan begrijpen hoe ze ermee kunnen rekenen. Maak zoveel mogelijk gebruik van echt materiaal. Hierdoor krijgt je kind meer inzicht in breuken. Denk bijvoorbeeld aan: pizza’s, taarten, repen chocolade, pannenkoeken, enz. Laat kinderen hier vooral ook mee experimenteren.

Enkele voorbeelden hiervan zijn:

Laat je kind koekjes verdelen over het gezin wanneer je gezellig thee drinkt op zondag;
Laat je kind de taart op zijn verjaardag aansnijden;
Laat je kind snoepjes verdelen met vriendjes;
En zo zijn er nog meer momenten waarop je breuken ter sprake kunt brengen.

Je kunt ook zelf materialen maken. Bewaar bijvoorbeeld dozen van pizza’s uit de winkel. Knip hier ‘pizza’s’ (cirkels) uit en verdeel deze in vier stukken. Je kunt dan oefenen met vierden. Dit kan natuurlijk ook met andere delen. Je kunt van papier ook stroken maken.

Maak vooral veel gebruik van ‘breukentaal’. Gebruik termen als halven, kwarten, verdelen.

Daarnaast is het belangrijk om met de leerkracht van je kind te bespreken hoe hij/zij breuken uitlegt. Zo kunnen jullie op dezelfde manier uitleg geven aan je kind.

Een leuk spel om breuken te oefenen is het ‘Breuken strokenspel’.