Breuken vermenigvuldigen: uitleg, oefenen en een handig schema


Je kind heeft hulp nodig bij vermenigvuldigen met breuken. Waar begin je met je uitleg? Niet voor niets vraagt je kind hulp bij het maken van vermenigvuldigen met breuken. Er is dus een stap of er zijn stappen die hij niet begrijpt of nog niet heeft onthouden.
Voor een kind is het leren van de stappen (de strategieën) van vermenigvuldigen met breuken extra moeilijk wanneer het de tafels nog niet heeft geautomatiseerd.
Als je kind nog niet zo gemakkelijk de keer- en deeltafels uit het hoofd kan opzeggen, is het ‘toegestaan’ om (een) tafelkaart(en) te gebruiken tijdens het rekenen met breuken. De uitleg is er immers om de stappen (de strategieën) van vermenigvuldigen met breuken onder de knie te krijgen. Daar kun je een ‘struikelblok’ als het niet goed beheersen van de tafels niet bij gebruiken. Om het vermenigvuldigen van breuken makkelijker te maken, kun je ook gebruikmaken van deze rekenregels.
Beter scoren op het moeilijke onderdeel breuken? Bekijk het complete pakket breuken met oefenboek en uitlegvideo’s voor je kind:
Check of je kind de termen ‘teller’, ‘noemer’ en ‘deelstreepje’ kent. De teller staat boven het deelstreepje en de noemer staat eronder. Vertel je kind ook dat het deelstreepje op twee verschillende manieren wordt geschreven:
1. de breuken in een rekenboek worden geschreven met een horizontaal deelstreepje:
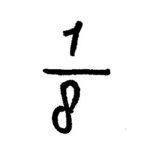
2. een computer gebruikt een diagonaal streepje:

Deze breuken betekenen hetzelfde, maar als je dat (nog) niet weet kan het zo verwarrend zijn.
Een breuk is niets anders dan dat er iets gebroken is. Van dat eerdere geheel heb je nu een aantal delen om mee te werken. Bijvoorbeeld:
Je bent jarig en hebt een taart gekocht. Er komen 7 mensen op bezoek. Je gasten krijgen een stuk taart en natuurlijk wil je zelf ook een stuk. Je snijdt de taart in 8 gelijke stukken. Eén stuk heet 1/8: het is 1 van de 8 stukken. Als je alle 8 stukken bij elkaar legt, heb je weer 1 hele taart.
1 : 8 = 1/8
8 x 1/8 = 8/8 = 1

Download hier de (gratis) Werkbladen Breuken Groep 6/7/8
Oefenbladen Rekenen Groep 7 (Gratis)
Gebruik 1 strategie voor het oplossen van de som
Vervolg je uitleg met het geven van een totaaloverzicht. Veel kinderen hebben daar baat bij. Vertel je kind wat het kan verwachten bij vermenigvuldigen met breuken en welke soort sommen er zijn.
Nog een laatste tip voordat de uitleg begint: een flink aantal kinderen heeft baat bij 1 strategie. Ik zal daarom, voor de duidelijkheid, in mijn uitleg 1 oplossingsstrategie gebruiken.
De volgende soort sommen komen in een rekenmethode van de basisschool aan bod:
Onderstaande vaardigheden worden bij het maken van deze sommen ook van je kind verwacht:
Heb je behoefte aan een overzicht van de soorten sommen en de bijbehorende strategieën? Onderaan het artikel heb ik alles in een schema (PDF) gezet dat je gratis kunt downloaden.

Breuken vermenigvuldigen met een breuk
Strategie = teller x teller en noemer x noemer.
Bijvoorbeeld:
1/4 x 1/2 = 1/8

De eerste stap is vermenigvuldigen, de tweede stap is de helen eruit halen, de derde stap is vereenvoudigen. Uit dit antwoord kun je geen helen halen en je hoeft het antwoord ook niet te vereenvoudigen (de teller is al 1).
Nog een voorbeeld:
1/4 x 2/5 = 2/20 = 1/10

Opnieuw volgen we de drie stappen:
- De eerste stap is vermenigvuldigen.
- De tweede stap is de helen eruit halen.
- De derde stap is vereenvoudigen.
Uit dit antwoord kun je geen helen halen, maar je kunt het antwoord wél vereenvoudigen (de teller en de noemer kun je door 2 delen).
Nog een voorbeeld:
10/3 x 3/9 = 30/27 = 1 3/27 = 1 1/9

Opnieuw volgen we de 3 stappen:
De eerste stap is vermenigvuldigen, de tweede stap is de helen eruit halen (de teller is groter (meer) dan de noemer, dus er zitten 1 of meer helen in het antwoord). De derde stap is vereenvoudigen (je kunt de teller én de noemer door 3 delen).
Vindt jouw kind het lastig om te bepalen wat het grootste getal is waardoor je de teller en noemer kunt delen? Geen nood, je kunt dan als tussenstap eerst de 2, 3 of 5 gebruiken om mee te delen. Soms ziet een kind na de eerste keer vereenvoudigen gemakkelijker dat het antwoord nog een keer gedeeld kan worden.
Zoals in de onderstaande som:
10/4 x 8/6 = 80/24 = 3 8/24 = 3 4/12 = 3 2/6 = 3 1/3
Je ziet dat je met een aantal keer vereenvoudigen toch tot hetzelfde eindresultaat komt. In een later stadium, als de strategie meer een automatisme is, kan een kind vaak grotere stappen maken om tot de oplossing te komen.
Breuken vermenigvuldigen met helen
Breuken vermenigvuldigen met een heel getal of omgekeerd
Strategie = de helen keer de teller.
De tussenstap = maak van de helen een breuk:
3 = 3/1
7 = 7/1
Een voorbeeld:
3 x 3/6 = 3/1 x 3/6 = 9/6 = 1 3/6 = 1 1/2

Stap 1: 3 x 3/6 = 9/6
Stap 2: je kijkt of je er helen uit kunt halen. Als de teller groter is dan de noemer, zit er tenminste 1 hele in. In 9/6 zit de 6 1 keer. Je hebt dus 1 hele (6 stukken van 1/6) en houdt 3/6 over.
Stap 3: vereenvoudigen. Van de breuk 3/6 kun je beide getallen delen door 3 → 1/2.
Omgekeerd ziet deze som er zo uit:
Strategie = de teller keer de helen.
De tussenstap = maak van de helen een breuk.
3/6 x 3 = als je van de helen een breuk maakt staat er: 3/6 x 3/1 = 9/6
Stap 2 is: je kijkt of je er helen uit kunt halen. 3/6 x 3/1 = 9/6 = 1 3/6
Stap 3 is: vereenvoudigen. Van de breuk 3/6 kun je de teller en de noemer beiden delen door 3 → 1/2 en wordt het antwoord 1 1/2.
Nog een voorbeeld:
1/4 x 40 (1/4 x 40/1) = 40/4 = 10
Omgekeerd blijft het antwoord het zelfde:
40 x 1/4 → 40/1 x 1/4 = 40/4 = 10
Heel getal + breuk (dit noemen we een gemengde breuk) vermenigvuldigen met een breuk
Let op: het wordt nu een beetje ingewikkelder.
De strategie = de helen keer de noemer (!) en dat getal optellen bij de teller van de breuk.

Visualisatie: maak het voor je kind meer inzichtelijk door de som te tekenen met behulp van de pizza(punten). Je tekent voor deze som: 5 hele pizza’s en die verdeel je elk in 3 stukken. Alle stukken worden gebruikt, je kunt ze dus allemaal een kleur geven. Dan teken je nog een pizza die verdeeld is in 3 stukken, maar daarvan kleur je maar 1 punt. Zo heb je 5 1/3 gevisualiseerd en ziet je kind snel dat het in deze som gaat over 16 punten van 1/3.

5 1/3 x 1/2 =
Tussenstap: voeg eerst de 5 helen toe aan de breuk:
(5 x 3) + 1 = 16
5 1/3 = 16/3
16/3 x 1/2 = 16/6 = 2 4/6 = 2 2/3

Hier geldt:
1. Zet het hele getal om in stukken zo groot als de noemer van de breuk die er direct naast staat: heel getal x noemer. (In het geval van bovenstaand voorbeeld: 5 x 3 = 15)
2. Tel de teller hierbij op: 15 + 1 = 16)
3. Maak de keersom: 16/3 x 1/2 = 16/6.)
4. Haal de helen eruit: 16/3 x 1/2 = 16/6 = 2 4/6.)
5. Vereenvoudig het antwoord: 16/3 x 1/2 = 16/6 = 2 4/6 = 2 2/3.)
Nog een voorbeeld:
6 1/4 x 1/3 → (6 x 4) +1 → 25/4 x 1/3 = 25/12 = 2 1/12
En nog een laatste voorbeeld:
7 1/7 x 9/10 = 50/7 x 9/10 =450/70 = 6 30/70 = 6 3/7

Gemengde breuken vermenigvuldigen
Nu is de stap naar een som met twee gemengde breuken niet zo moeilijk meer.
Heel getal + breuk vermenigvuldigen met een heel getal + breuk (twee gemengde breuken).
Strategie = de helen x de noemer en dat getal optellen bij de teller van de breuk.
1 1/2 x 1 1/5 =
Ook hier geldt:
1. Zet de hele getallen om in stukken zo groot als de noemer van de breuk die er direct naast staat (heel getal x noemer).
2. Tel de teller hierbij op.
3. Maak de keersom.
4. Haal de helen er uit.
5. Vereenvoudig het antwoord.
Dat ziet er dan zo uit:
1 1/2 x 1 1/5 → (1 x 2) + 1 = 3 en (1 x 5) + 1 = 6 → 3/2 x 6/5 = 18/10 = 1 8/10 = 1 4/5

Nog een voorbeeld:
1 7/8 x 5 1/5 = 15/8 x 26/5 = 390/40 = 9 30/40 = 9 3/4
Je ziet dat dit erg grote getallen worden… dat rekent niet gemakkelijk. Kan het makkelijker? Ja! Door de strategie “wegstrepen” in te zetten. Wat houdt wegstrepen precies in?
Wegstrepen
Wegstrepen is niets anders dan een teller en noemer door het zelfde getal delen voordat je verder gaat met je berekening.
Let er op dat je je kind uitlegt dat wat onder de streep gedeeld wordt, ook boven de streep met hetzelfde getal moet gebeuren. Dit mag in een zelfde breuk maar het mag ook kruislings gebeuren. Dus, in dit voorbeeld streep ik de teller van het eerste getal weg tegen de noemer van het andere getal. Ik neem bovenstaande breuk als voorbeeld:
1 7/8 x 5 1/5 = 15/8 x 26/5 = 3/8 x 26/1 = 78/8 = 9 6/8 = 9 3/4

In het schuin- en vetgedrukte gedeelte van de som heb ik een teller en noemer met hetzelfde getal gedeeld: 15 en 5 door 5. Ik streepte ze weg en kreeg de bovenstaande variant op de som. Toch kreeg ik hetzelfde antwoord!
Nog een voorbeeld:
6 1/8 x 3 3/7 = 49/8 x 24/7 = 7/8 x 24/1 = 7/1 x 3/1 = 21/1 = 21

In deze som heb ik zelfs 2 keer weggestreept één keer door te delen door 7 en één keer door te delen door 8. Hierdoor is de som veel gemakkelijker door je kind uit te rekenen.
En dan nu de laatste variant van vermenigvuldigen met breuken.
Heel getal + breuk vermenigvuldigen met een heel getal (een gemengde breuk)
Je kunt dit soort sommen op 2 verschillende manieren uitrekenen. Maar omdat ik heb vastgesteld dat veel kinderen baat hebben bij 1 soort uitleg, beperk ik me tot het uitleggen van de gemakkelijkste manier.
7 x 4 1/2 = 28 7/2 = 31 1/2
Strategie: eerst doe je de helen x de helen → 7 x 4 = 28
Daarna doe je de helen x de teller (!) → 7/1 x 1/2 =7/2
Nu kun je de helen uit de uitkomst halen: 28 7/2 = 31 1/2.
In deelstapjes ziet deze som er als volgt uit:
Stap 1:
De helen keer de helen: 7 x 4 = 28
De helen keer de teller: 7/1 x 1/2 = 7/2
Dus 7 x 4 1/2 = 28 7/2
Stap 2: je kijkt of je helen uit de breuk kunt halen.
Het antwoord is ja: in 7/2 zitten 3 helen (3 x 2 = 6) en houd je 1/2 over (rest 1)
Het antwoord is nu 31 1/2.
Stap 3: vereenvoudigen.
Deze breuk kun je niet meer vereenvoudigen, de teller is al 1.
Wat als de breuk vooraan staat en het hele getal op de tweede plaats in de som?
1/4 x 40 =
Hier staat eigenlijk: 1/4 x 40/1 → 1 x 40 = 40 en 4 x 1 = 4 → 1/4 x 40/1 = 40/4 = 10
Ook bij de volgende som volg je de stappen:
Helen keer helen en teller keer de helen.
2 1/3 x 12 = →
Helen keer de helen: 2 x 12 = 24
Teller keer de helen: 1 x 12 → 12/3
Dus 2 1/3 x 12 = 24 12/3 = 28
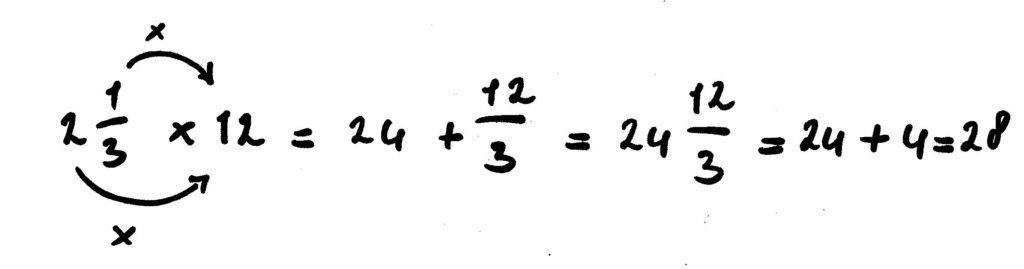
Een laatste voorbeeldsom waarbij je helen met een breuk vermenigvuldigt:
5 7/9 x 3 =
Strategie:
1. De helen keer de helen en de teller keer de helen.
2. Helen uit de breuk halen.
3. Vereenvoudigen.
1. 5 x 3 = 15 en 7 x 3 = 21
Het antwoord op stap 1 is: 15 21/9
2. De 9 past twee keer in de 21 en dan houd je drie stukken van 1/9 over.
Het antwoord is: 2 3/9. Dit getal tel je bij de helen op die je al had, in dit voorbeeld bij de 15 helen. Het antwoord wordt dan: 17 3/9.
3. 17 3/9, deze breuk kun je nog vereenvoudigen. 3 en 9 kun je beide door 3 delen. Het antwoord wordt dus: 17 1/3.
5 7/9 x 3 = 15 21/9 = 17 3/9 = 17 1/3
Breuken vermenigvuldigen met hele getallen
De meeste fouten worden gemaakt doordat een kind de onderstaande strategieën door elkaar haalt. Visualisatie (tekenen) is samen met zeer regelmatig kort oefenen vaak de oplossing.

Voorbeeld:
3/5 x 4

Breuken vermenigvuldigen met een heel getal of omgekeerd.
Strategie = de helen x de teller → 4 x 3 = 12 → 3/5 x 4 = 12/5 = 2 2/5
Eventuele tussenstap = maak van de helen een breuk, 4 = 4/1, 7 = 7/1, enzovoort. Dan volgt teller x teller en noemer x noemer.

Download het schema als PDF-bestand

Wil je liever breuken oefenen met lego? Download hier het PDF-bestand.
Download hieronder gratis oefenbladen voor rekenen!
Oefenbladen Rekenen Groep 7 (Gratis)
Oefenbladen Rekenen Groep 8 (Gratis)
Meer uitleg over breuken?
Gerelateerde artikelen
Reacties
10 reacties op “Breuken vermenigvuldigen: uitleg, oefenen en een handig schema”-
wat moet je doen als je helen hebt bij een breuk bijvb. 3 6/24 x 6 8/6
-
Hoi Merrryy,
Je haalt eerst de helen uit de laatste breuk:
6 8/6 = 7 1/3
Dan vereenvoudig je de andere breuk:
3 6/24 = 3 1/4
Dan wordt de ssom:
3 1/4 x 7 1/3 =
Van 3 1/4 maak je allemaal vierden:
3 = 12/4
In totaal heb je dan 13/4
Van 7 1/3 maak je allemaal derden:
7 = 21/3
In totaal heb je dan 22/3.
De som wordt dan:
13/4 x 22/3 =
Nu kun je de tellers en de noemers met elkaar vermenigvuldigen:
13 x 22 = 286
4 x 3 = 12
13/4 x 22/3 = 286/12 = 23 5/6Groetjes,
Carola
-
-
hoi ik vind sommen zoals 8×3/4 heel lastig kunt u mij het uitleggen
-
Hoi JDraakje,
Dat zijn ook lastige sommen!
Je maakt van 8 eerst een breuk: 8/1. (1/1 is 1 hele en 8/1 zijn 8 helen.)
Dan krijg je: 8/1 x 3/4 =…..
Dan doe je de teller (het getal boven de breukstreep) van de ene breuk keer de teller van de andere breuk en de noemer van de ene breuk keer de noemer van de andere breuk. Je krijgt dan:
8/1 x 3/4 = 24/4= 6.
Als je dit lastig vindt door de schuine breukstrepen, kun je het beste nog even kijken naar het voorbeeld hierboven.
Succes!
Groetjes,
Carola
-
-
ik snap er niks van
-
Hoi Kim, wat precies snap je niet? Misschien dat ik het je kan uitleggen.
Groetjes,
Carola
-
-
hoi ik vind de breuken heel lastig
-
Hoi Dylan,
Dat kan ik me goed voorstellen! Als je een vraag hebt, kun je hem altijd stellen. Hier of even via de e-mail: [email protected]Groetjes,
Carola
-
-
Heeft u ook een omreken tabel van m3 naar bv liters
-
Hallo Angelique,
In dit artikel lees je hoe je inhoudsmaten omrekent: https://wijzeroverdebasisschool.nl/uitleg/meten
Succes!Hartelijke groet,
Carola
-









Marieke Kegels –
Handige tips en het werkboek is heel duidelijk.