Procenten berekenen: hoe doe je dat?


Hoe bereken je procenten? Om die vraag te beantwoorden, moet je eerst weten wat procenten precies zijn. Pas dan kun je starten met procenten berekenen.
In dit artikel krijg je heldere uitleg over procenten berekenen, zodat je jouw kind(eren) kunt helpen met rekenen oefenen!
Vanaf het rekenen in groep 7 maakt je kind kennis met procenten uitrekenen. Veel kinderen vinden dit moeilijk. Andere rekenproblemen spelen vaak mee:
- Je kind begrijpt de relatie tussen verhoudingen, breuken, kommagetallen en procenten niet. In dat geval raden we je aan de uitleg in het artikel Van breuken naar procenten en kommagetallen nog eens te lezen.
- Je kind heeft moeite met delen door 10 en 100. Het weet niet goed waar ‘de komma dan naartoe moet’ (zie verderop in dit artikel).
- Je kind leest de vraag niet goed. In verhaalsommen wordt de ene keer gevraagd ‘hoeveel je er krijgt’ en een andere keer ‘hoeveel je dan moet betalen’. Als je kind de vraag niet goed leest, weet het ook niet welk antwoord het moet geven. Laat je kind in dat geval werken met een stappenplan.
Oefenbladen Procenten Groep 7/8 (Gratis)
Wat zijn procenten?
Voor procenten geldt hetzelfde als voor breuken: ze zijn een deel van een geheel. Bij een taart die in 3 stukken is verdeeld, heten de stukken één derde, oftewel 1/3, oftewel 1 van de 3 stukken.
Een procent is dus niets meer of minder dan 1 van 100, dus 1/100 (spreek uit: één honderdste).
Maar waarom worden er 2 manieren gebruikt om hetzelfde op te schrijven? Omdat boven een breukstreep geen kommagetal mag staan. De breuk 12,5/100 bestaat niet. Dat schrijf je dus als 12,5%.

Een procent is uit te drukken in een percentage. Dat wil zeggen:
als je hebt uitgerekend dat iets bijvoorbeeld 25% is, dan is het percentage 25.
Een procent is een breuk die altijd 100 als noemer heeft. De noemer van een breuk geeft aan in hoeveel stukjes iets is verdeeld. Bij procenten gaat het dus altijd om een geheel dat in 100 stukjes is verdeeld.

1 procent is dan één van die stukjes. Het gele hokje is dus 1 procent van het hele vierkant.
1% = 1/100

Hier zijn 10 hokjes gekleurd, dus: 10/100, oftewel 10%. Je ziet ook dat het 1 rij is van de 10 rijen, dus je kunt ook zeggen dat het 1/10 is.
10% = 10/100 = 1/10

Hier zijn 25 hokjes gekleurd. 25 van de honderd, dus 25/100 of 25%. Je ziet dat het gekleurde stukje 4 keer in het hele vierkant gaat. Het is dus 1/4.
25% = 25/100 = 1/4

Hier zijn 50 hokjes gekleurd. 50 van de honderd, dus: 50/100 of 50%. Je ziet ook dat de helft gekleurd is, dus ½.
50% = 50/100 = 1/2
Het is belangrijk dat je kind eerst goed snapt wat procenten zijn voordat het begint met rekenen met procenten. Bovendien snapt je kind met deze basisinformatie al veel berichtgeving over percentages en weet hij wat een ‘klein percentage’ is, bijvoorbeeld in dit bericht van het Jeugdjournaal: Kleine groep kinderen drinkt te veel energiedrankjes.
Procenten berekenen: de 3 soorten sommen
Wat procenten berekenen vaak lastig maakt, is dat er zoveel verschillende soorten opgaven lijken te zijn. Maar eigenlijk zijn alle opgaven terug te brengen tot 3 soorten:

Als je de informatie uit de opgave ordent in een verhoudingstabel, wordt snel duidelijk wat voor soort som het is en hoe je hem moet uitrekenen. Een vaste aanpak (de nr. 1 aanpak!) met de verhoudingstabel maakt het allemaal een stuk overzichtelijker.
Oefenen met de verhoudingstabel en procenten? Bekijk de Spoedcursus Procenten:
Bekijk ook:
Oefenbladen Procenten Groep 7/8 (Gratis)
Problemen bij procenten uitrekenen
Als je kind in groep 7 met de procenten begint, leert het eerst bovenstaande percentages in combinatie met de breuken. Je kind leert dat je 10% kunt uitrekenen door het getal door 10 te delen.
Voorbeeld:
Op een broek van €85,00 krijg je 10% korting. Hoeveel kost de broek nu?
10% betekent: delen door 10, dus €8,50 korting. De broek kost nu dus €85,00 – €8,50 = €76,50.
Als je kind deze som uitrekent, kan het tegen 2 problemen aanlopen:
- 1. je kind weet niet hoe je 85 deelt door 10 (dat de komma dan 1 plekje naar links moet).
Oefen dit apart:
Als er geen komma staat in het getal, zet je die achter het getal.
Delen door 10: komma 1 plaats naar links.
Delen door 100: komma 2 plaatsen naar links, enzovoort.
Voorbeeld:

2. Je kind leest de vraag niet goed, en rekent alleen de korting uit.
Als bovenstaande problemen optreden, vindt je kind de sommen met procenten al heel snel moeilijk. Het denkt misschien dat het niet goed kan rekenen met procenten, terwijl het grootste probleem ergens anders ligt. Bepaal daarom altijd waar de moeilijkheid voor je kind precies zit.
Wanneer je kind geen problemen meer heeft met het percentage 10%, kan het op dezelfde manier aan de slag met de percentages 25% (door te delen door 4), 50% (door te delen door 2) en 1% (door te delen door 100).
Daarna komt de 75% aan de orde. Dat is dus 50% + 25% of 3 x 25%.

Als ook dit lukt, kun je allerlei combinaties maken: 5% is de helft van 10%, 15% is dan weer 10% + 5%, 60% is 10% x 6 enzovoorts. De meeste kinderen komen op deze manier een heel eind. Maar op een gegeven moment moet er ook gerekend worden met percentages van bijvoorbeeld 36%.
Dan kun je natuurlijk 3 x 10% doen, en dan 6 x 1% erbij. Maar makkelijker is het om eerst 1% uit te rekenen, en dat x 36 te doen. Dat is een manier die altijd werkt!
Dus als jouw kind niet zo makkelijk ziet dat 75% hetzelfde is als 3 x 25%, of moeite heeft met het delen door 4, dan kan het ook altijd 1% uitrekenen en dat vermenigvuldigen met 75.
Voorbeeld:
75% van 320 kinderen van de school heeft een mobiele telefoon. Hoeveel kinderen zijn dat?
We ordenen de informatie eerst in een verhoudingstabel. In onderstaande verhoudingstabellen staan steeds de gegevens uit de opgave onderstreept.


Beide methodes werken. Bij de eerste methode moet je kind 320 delen door 4 en dat is voor sommige kinderen lastig. Bij de tweede methode moet er vermenigvuldigd worden met een kommagetal, en ook dat kan lastig zijn. Door de opgave in een verhoudingstabel te zetten, wordt in ieder geval overzichtelijk wat je kind moet uitrekenen.
Lees hier meer over procenten berekenen met een verhoudingstabel.
Zeker bij verhaalsommen is het daarom aan te raden om altijd een verhoudingstabel te gebruiken als het over procenten berekenen gaat. Het is een goede manier om de informatie uit de som te ordenen.
Hoeveel is een bepaald percentage?
Hieronder volgen een paar voorbeelden van sommen waarbij je moet uitrekenen hoeveel een bepaald percentage is.
Van geheel (100%) naar deel
In een wijk wonen 2500 mensen. 60% hiervan zijn vrouwen. Hoeveel mannen wonen er?
Je weet dat er in totaal 2500 mensen zijn. 2500 is dus 100%. 60% is vrouw, 40% is man. In dit geval weet je de 100% (het geheel) en moet je 40% (deel) uitrekenen.

In dit geval is de makkelijkste manier via de 10%, omdat het gevraagde percentage ook een tiental is.
Van geheel naar deel, winst berekenen
Frank koopt een tweedehands fiets voor € 820,00. Hij knapt hem op en verkoopt hem met 22% winst. Voor hoeveel heeft hij hem verkocht?
Om te voorkomen dat je kind alleen de winst berekent, is het handig om eerst een ‘plannetje’ te maken:
De verkoopprijs is de inkoopprijs + de winst, dus €820 + winst =
Winst berekenen: eerst vul je in wat je al weet en wat je moet uitrekenen (de onderstreepte getallen). Het inkoopbedrag is 100%. Je moet weten hoeveel 22% daarvan is. Het is het handigst om dat uit te rekenen door eerst te berekenen hoeveel 1% is. Daarna vermenigvuldig je die uitkomst met 22. De verhoudingstabel ziet er dan zo uit:

Als je kind nu nog even terugkijkt naar het oorspronkelijke plannetje, ziet het dat het die €180,40 bij het inkoopbedrag moet optellen. De fiets is dus verkocht voor €820 + €180,40 = €1000,40.
Rekenen met percentages boven de 100%
Bovenstaande som had ook op een andere manier opgelost kunnen worden. De koper van de fiets betaalt namelijk eigenlijk 122% (100% + 22%) van de oorspronkelijke prijs. Dus de berekening had er ook als volgt uit kunnen zien:

Prijs exclusief btw berekenen
Op dezelfde manier kan ook uitgerekend worden hoeveel de prijs van iets is zonder de btw.
Voorbeeld:
In de folder staat een spel voor €48,40 (inclusief btw). De btw is 21%. Wat kost het spel zonder de btw?
Voor het spel is eigenlijk 121% betaald. Dus:

Prijs inclusief btw berekenen (geheel naar deel)
Op een website staan de prijzen zonder btw vermeld. Er staat een partij frisdrank te koop voor €172 exclusief btw. Wat is de prijs inclusief 21% btw?
Deze som kan uitgerekend worden via de 1%-manier, dus:

Dan moet de €36,12 nog opgeteld worden bij €172. Daarmee kom je uit op €208,12.
Maar het gaat sneller als je bedenkt dat €172 100% is, en dat je 121% moet betalen. Dus:

Procenten berekenen: naar 100% rekenen via 1% (deel naar geheel)
Gerard heeft nog €130,00 over van zijn spaargeld. Dat is nog maar 2% van wat hij eerst had. Hoeveel had hij eerst?
Eerst vul je de informatie uit de som in. In dit geval weet je het deel (2%) en moet je het geheel (100%) uitrekenen.

De volgende opgave lijkt lastiger, maar je rekent hem eigenlijk op dezelfde manier uit.
In de uitverkoop is een jas 20% afgeprijsd. Hij kost nu €72,00. Hoe duur was hij eerst?

Deze opgave wordt een stuk makkelijker als je bedenkt dat je maar 80% van de oorspronkelijke prijs betaald hebt. Je weet het deel (80%) en moet het geheel uitrekenen. Dan hoef je alleen maar in de verhoudingstabel te zetten wat je weet. Daarna reken je de som op dezelfde manier uit als de som hierboven.
In dit geval had je ook kunnen delen door 80 om 1% te berekenen en dat vervolgens x 100 doen om bij de 100% te komen. Het antwoord blijft hetzelfde.
Percentages uitrekenen
Bij bovenstaande sommen zijn de percentages steeds aangegeven, en moet je uitrekenen hoeveel zo’n percentage waard is. Maar er zijn ook sommen waarbij je juist de percentages moet uitrekenen, zoals bij het berekenen van een korting.
Een stoel is in de aanbieding van €620 voor €527. Hoeveel procent korting is er gegeven?
Bereken eerst het verschil tussen de oude en de nieuwe prijs. Dat is: € 620 – € 527= € 93.
Nu moet je de vraag ‘hoeveel procent is € 93 van € 620?’ beantwoorden. Je zetten de informatie die je al hebt weer in een verhoudingstabel (hier onderstreept).
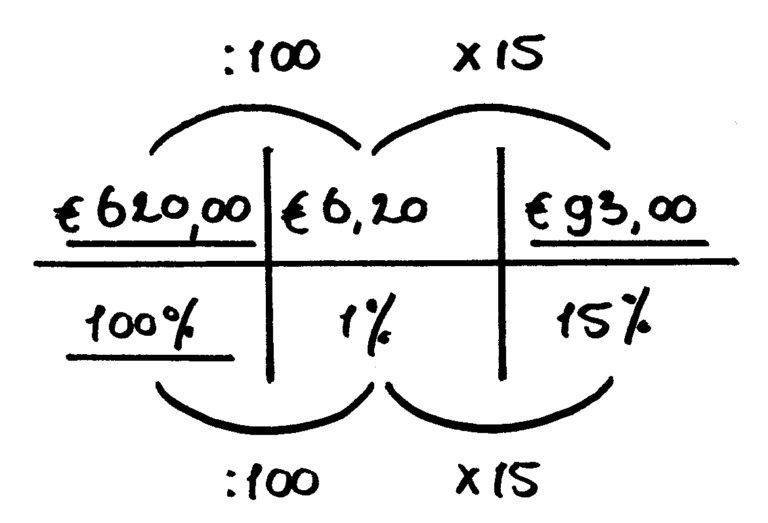
Daarna reken je eerst 1% uit. Vervolgens bereken je hoeveel keer € 6,20 in € 93 past. Dat is dus een deelsom: 93 : 6,20 = 15. Dat betekent dat € 93 hetzelfde is als 15%!
Percentage berekenen van een verhouding
Voorbeeld 1:
In een klas van 25 kinderen zijn 5 kinderen ziek. Hoeveel procent is dat?

5 van de 25, dat is 20 van de 100, oftewel: 20/100, oftewel: 20%.
Voorbeeld 2:
Van de 640 appels zijn er 128 rot. Hoeveel procent is dat?
Eerst weer invullen wat je al weet. Alle appels bij elkaar zijn 100%. 640 is dus 100%.

Daarna is het vaak een beetje uitproberen: neem je 1% en kijk je hoe vaak dat in 128 gaat? Als je dat doet, moet je rekenen met een kommagetal. 10% is in dit geval makkelijker!
Percentage prijsstijging berekenen
Soms weet je de nieuwe prijs en de oude prijs en moet je uitrekenen met hoeveel procent de prijs is gestegen.
Voorbeeld:
De benzineprijs is binnen 1 jaar tijd gestegen van € 1,20 naar € 1,44 per liter. Hoeveel procent prijsstijging is dat?
Je rekent eerst uit hoe groot het verschil is tussen de twee prijzen: 1,44 – 1,20 = 0,24. Het verschil is dus € 0,24. Nu is de vraag hoeveel procent dat is van de oude prijs.

De benzineprijs is dus met 20% gestegen.
Procenten berekenen: van breuk naar percentage
In de opgave over de appels zou het ook voor de hand liggen om uit te rekenen hoe vaak 128 in 640 past. Nadeel hiervan is dat uit een deling geen percentage komt, maar het getal 5. Je zou dus kunnen zeggen dat 128 1/5 deel is van 640. Maar dan moet je nog van de breuk naar het percentage. Hoe doe je dat?
Eigenlijk is het omrekenen van een breuk naar een percentage niets anders dan een breuk omrekenen naar een andere breuk, namelijk naar honderdsten.
In het voorbeeld van de klas hierboven waren 5 kinderen ziek van de 25. 5 van de 25 is hetzelfde als 20 van de 100, dus: 20%.
Zo kan iedere breuk omgerekend worden naar een percentage, maar bij sommige breuken is dat lastiger dan bij andere.
Voorbeeld:
Van de 30 kinderen in de klas spelen er 10 een muziekinstrument. Welk percentage is dat?

In dit voorbeeld moet je dus uitrekenen hoe vaak 30 in de 100 gaat (dus eigenlijk 100 delen door 30). Dat is ongeveer 3,33 keer.
Wat je onder doet, moet je ook boven doen. Hier zie je dus de breuk 33,3 honderdsten, oftewel 33,3%.
Omdat dit zo lastig uit te rekenen is, leert je kind op school de vaste combinaties tussen de breuken en de procenten. Hierbij staan ook de kommagetallen die erbij horen. Want ieder percentage en iedere breuk is ook te schrijven als kommagetal. 33/100 kun je bijvoorbeeld ook schrijven als 33%, maar ook als 0,33.

Promille berekenen
Rekenen met promilles is niet echt basisschoolstof. Maar omdat je kind het soms toch tegenkomt in teksten: een promille is 1/1000 deel. ‘Pro’ betekent ‘per’, en ‘mille’ betekent ‘1000’. Per duizend dus.
Als je 1 promille wilt berekenen, moet je dus delen door 1000.
FAQ
Je kunt procenten berekenen door eerst 1% uit te rekenen. Je deelt dan het getal door 100. Vervolgens vermenigvuldig je de uitkomst met het percentage dat je wilt weten. Bijvoorbeeld 41% van 200. Eerst bereken je 1% van 200. 200 : 100 = 2. Dan doe je 41 x 2 = 82.
Een percentage van een bedrag bereken je door eerst 1% van het bedrag uit te rekenen. Vervolgens vermenigvuldig je de uitkomst met het percentage. Bijvoorbeeld 30% van € 150. Eerst bereken je 1 % van € 150. Dat is € 1,50. Daarna doe je € 1,50 x 30 = € 45.
Je rekent uit hoeveel procent twee bedragen (of getallen) van elkaar zijn door eerst 1% te berekenen. Bijvoorbeeld: hoeveel procent is 93 van 620? Eerst bereken je 1% van 620. Dat is 6,20. Vervolgens kijk je hoeveel keer 6,20 in 93 past (15 keer). Het antwoord is dus 15%. Je kunt dit berekenen met een verhoudingstabel.
Je kunt procenten oefenen met een vaste aanpak (zie het artikel hierboven). Er zijn drie soorten sommen met procenten die je met deze formule kunt oplossen. Wil jij binnen 2 weken alle soorten sommen kunnen oplossen? Volg dan de spoedcursus procenten!
Oefenbladen Rekenen Groep 7 (Gratis)
Oefenbladen Rekenen Groep 8 (Gratis)
Gerelateerde artikelen
Reacties
10 reacties op “Procenten berekenen: hoe doe je dat?”-
Bedankt, deze info heeft me zeer hard geholpen.
-
Graag gedaan Daan! Fijn om te horen!
Hartelijke groet,
Carola
wijzeroverdebasisschool.nl
-
-
Hallo Lisa,
Dat klopt inderdaad! De kinderen op de basisschool leren dit alleen nog niet. Vandaar dat we het in dit artikel niet noemen.Hartelijke groetjes,
Carola -
Hoi Maaike, met o.a. jouw bijdragen heb ik Lynn drie jaar rekenbijles gegeven. Ze heeft de citotoets afgelopen schooljaar goed gemaakt, ook voor rekenen dus. Advies Cito was havo/vwo, terwijl ze met een grote rekenachterstand bij mij begon toen ze nog in groep 6 zat Super toch! Ik heb veel aan jouw aanwijzingen gehad. Dank je wel daarvoor. Nu werk ik met een jongen die over is van groep 7 naar groep 8, Ruben heet hij. Het rekenen gaat ook steeds beter bij hem. Dank , Maaike, voot jouw didaktische aanwijzingen het afgelopen jaar en ook nu weer dit jaar. Ik ben zelf docent havo/vwo geweest en waardeer jouw aanwijzingen enorm. Met een groet,
Beert-
Beste Beert,
Dank voor je bericht. Wat mooi om te horen!
Succes met Ruben!Hartelijke groet,
Carola
-
-
Wij zijn erg enthousiast over de geheugenkaartjes/schema’s en de filmpjes!! DANK!
-
kan je naar kader als je eerst op cito dat had dan weer hoog ?
-
Dat is van een afstand lastig om te zeggen, omdat ook de werkhouding, zelfstandigheid en motivatie belangrijk zijn bij het bepalen van een advies. Je kunt dit het beste even op school navragen.
Succes!
Hartelijke groet,
Carola -
Hoi Jeee,
Fijn dat je het iets beter snapt dan eerst. Als je vragen hebt, kun je ons altijd even mailen: [email protected].
Succes!Groetjes,
Carola
-
-
-
Beste Peter,
Dank voor je reactie. Aanvullingen op de artikelen zijn altijd van harte welkom! We kunnen de extra uitleg dan in het artikel plaatsen. Als dit niet lukt met de editor uit het reactieveld dan kan het ook gemaild worden naar [email protected]. Dit artikel geeft inderdaad alleen de basis weer. We zullen kijken of we dit artikel een keer kunnen aanvullen met meerdere oplossingen (input is van harte welkom want we zijn ook druk bezig met veel nieuwe artikelen). Hartelijke groet, Maaike










Marieke Kegels –
Handige tips en het werkboek is heel duidelijk.